3. КИНЕТОСТАТИЧЕСКОЕ ИССЛЕДОВАНИЕ

РЫЧАЖНОГО МЕХАНИЗМА ДВУХЦИЛИНДРОВОГО ДВИГАТЕЛЯ ТРАКТОРА. ИССЛЕДОВАНИЕ

ДВИЖЕНИЯ МЕХАНИЗМА

3.1 Определение сил и моментов сил, действующих на звенья механизма

Вычертим кинематическую схему и план положений механизма в масштабе длин план скоростей в масштабе план ускорений в масштабе и индикаторную в масштабе

(3.1)

где P_max — заданное максимальное индикаторное давление , МПа;

h — принятая высота индикаторной диаграммы, мм.

Подставляя численные значения в уравнение (3.1), получим

По диаграмме усилий, в соответствии с разметкой хода рабочего звена, определяем индикаторное давление для каждого из положений механизма. Для этого строим диаграмму усилий, разместив ось перемещений S параллельно оси перемещения рабочего органа. Проводя из каждой точки положения ползуна прямые, параллельные оси P, получим на диаграмме разметку положений точек B и D. При этом необходимо учесть, что нумерация положений на диаграмме должна соответствовать направлению рабочего и холостого хода.

Величину давления определяем из уравнения

(3.2)

где у — ордината диаграммы для заданного положения, мм.

Сила давления газа на поршень:

, (3.3)

где Р – удельное давление газа на поршень в Па (1 Па=1 Н/м)

d – диаметр поршня в м.

Найдём значения сил для расчётного первого положения.

Вычислим силы давления газа на поршень по формуле (3.3). Удельное давление газа на поршень определяется по формуле:

Для точки B:

Для точки D:

Силы тяжести звеньев приложены в их центрах тяжести и определяются по формуле:

(3.4)

где m — масса i-го звена, кг;

g — ускорение свободного падения, равное 9,81 м/с².

Подставляя численные значения, определим величины сил тяжести звеньев:

Силы инерции звеньев приложены в их центрах масс и определяются по формуле:

(3.5)

где — ускорение центра масс i-го звена,

Знак «минус» показывает, что направление силы инерции противоположно направлению вектора ускорения центра масс звена .

Подставляя численные значения, определим величины сил инерции звеньев для заданного положения механизма:

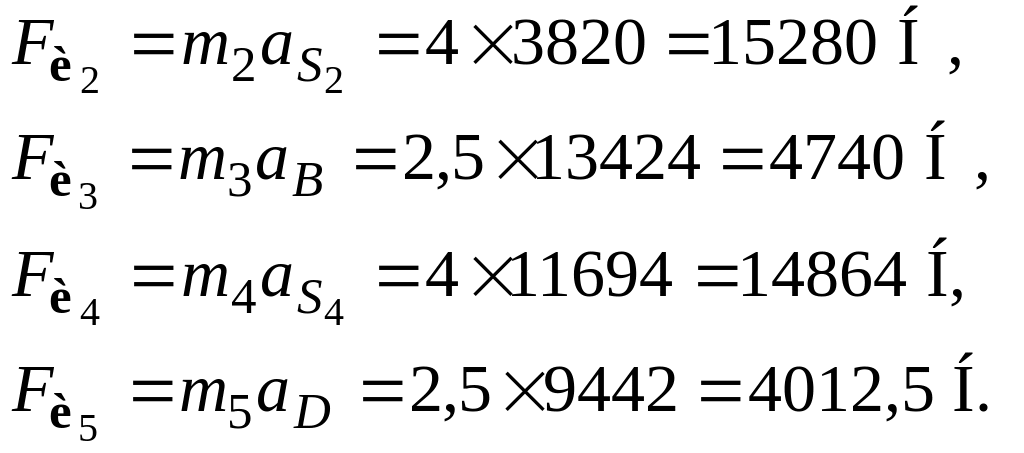
Сила инерции 1-го звена равна нулю, т.к. ускорение

Моменты сил инерций (инерционные моменты) звеньев определяем по формуле:

(3.5)

где — угловое ускорение i-го звена, с^-2;

— момент инерции i-го звена относительно оси, проходящей через центр масс перпендикулярно к плоскости движения который определяется по формуле:

. (3.6)

Знак «минус» в уравнении (3.5) показывает, что направление момента сил инерций противоположно направлению углового ускорения .

Подставляя численные значения в (3.6), получим:

Тогда величины моментов сил инерций звеньев:

Определение реакций в кинематических парах начинаем с группы Ассура, состоящей из звеньев 2, 3.

3.2 Силовой расчет группы Ассура, состоящей из звеньев 2 и 3

Группу, состоящую из звеньев 2 и 3, вычерчиваем отдельно в масштабе длин и в соответствующих ее точках прикладываем силы тяжести, силы инерции звеньев и моменты сил инерций. Отброшенные связи заменяем реакциями (реакция воздействия звена 1 на звено 2) и (реакция воздействия направляющей 0 на звено 3).

Под действием внешних сил, сил инерции и реакций группа будет находиться в равновесии.

Составляем условие равновесия группы, пр иравнивая к нулю сумму всех сил, действующих на группу:

(3.14)

Неизвестными в данном уравнении являются реакции и .

Линия действия реакции известна: она перпендикулярна направляющей Ох (без учета сил трения). Величину данной реакции определим, если зададимся ее направлением, и решим уравнение моментов всех сил, приложенных к звеньям 2 и 3 относительно точки А:

или

(3.15)

Выражая из данного уравнения реакцию , получим

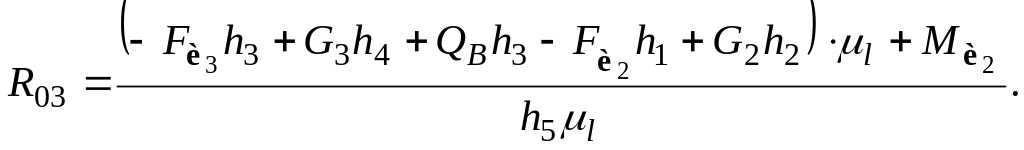
Подставляя численные значения, получим

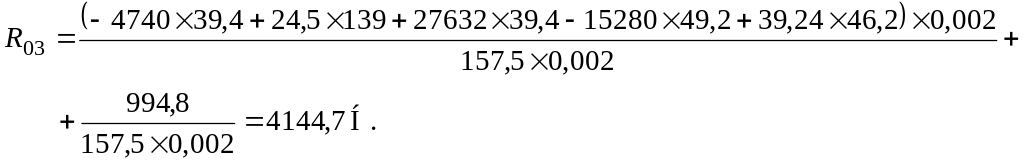
Поскольку значение получено со знаком «плюс», то направление реакции выбрано правильно.

Для определения реакции строим план сил в масштабе

На свободном поле листа ставим точку a, из которой параллельно силе откладываем вектор , длина которого

Из конца вектора в направлении силы откладываем вектор ,

Из точки c в направлении силы инерции откладываем вектор , длиной

Далее из точки d в направлении силы откладываем вектор ,

Из конца вектора в направлении силы откладываем вектор ,

Из точки f в направлении силы откладываем вектор ,

Соединив точку g с точкой а на плане сил, получим вектор , изображающий на плане сил искомую реакцию , величина которой

3.3 Силовой расчет группы Ассура, состоящей из звеньев 4 и 5

Группу, состоящую из звеньев 4 и 5, вычерчиваем отдельно в масштабе длин и в соответствующих ее точках прикладываем силы тяжести, силы инерции звеньев и моменты сил инерций. Отброшенные связи заменяем реакциями (реакция воздействия звена 1 на звено 4) и (реакция воздействия направляющей 0 на звено 5).

Под действием внешних сил, сил инерции и реакций группа будет находиться в равновесии.

Составляем условие равновесия группы, пр иравнивая к нулю сумму всех сил, действующих на группу:

(3.14)

Неизвестными в данном уравнении являются реакции и .

Линия действия реакции известна: она перпендикулярна направляющей Ох (без учета сил трения). Величину данной реакции определим, если зададимся ее направлением, и решим уравнение моментов всех сил, приложенных к звеньям 4 и 5 относительно точки B:

или

(3.15)

Выражая из данного уравнения реакцию , получим

Подставляя численные значения, получим

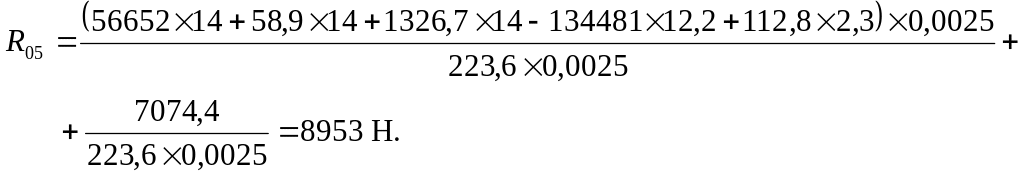
Поскольку значение получено со знаком «плюс», то направление реакции выбрано правильно.

Для определения реакции строим план сил в масштабе

На свободном поле листа ставим точку a, из которой параллельно силе откладываем вектор , длина которого

Из конца вектора в направлении силы откладываем вектор ,

Из точки c в направлении силы инерции откладываем вектор , длиной

Далее из точки d в направлении силы откладываем вектор ,

Из конца вектора в направлении силы откладываем вектор ,

Из точки f в направлении силы откладываем вектор ,

Соединив точку g с точкой а на плане сил, получим вектор , изображающий на плане сил искомую реакцию , величина которой