Методические указания по темам курса

Тема 1. Группировка материалов наблюдений

Группировкой называется расчленение единиц совокупности на однородные группы по определенным, существенным для них признакам. Группировка является важнейшим статистическим методом обобщения статистических данных, основой применения других методов статистического анализа.

Группировки могут быть построены по какому-то одному или нескольким существенным признакам. В зависимости от вида группировочных признаков различают группировки атрибутивные (качественные) и количественные.

Число групп зависит от задачи исследования, вида признака, степени вариации признака, численности совокупности. Если признак носит дискретный характер и может принимать ограниченное число значений, количество групп, как правило, равно количеству возможных значений. Если признак является непрерывной величиной или дискретной, которая может принимать очень большие значения (например, численность работников на предприятии), то число групп будет зависеть от диапазона изменения признака, от объема совокупности. Определить число групп можно с помощью формулы:

n = 1 +3,322 lg N,

где n – число групп; N – число единиц совокупности.

Интервал – это значение варьирующего признака в определенных границах. Каждый интервал имеет величину, верхнюю и нижнюю границу или одну из них. Нижняя граница – наименьшее значение признака в интервале, верхняя граница – наибольшее. Величина интервала – разность между верхней и нижней границами интервала. Интервалы группировки по величине бывают равные и неравные. Равные интервалы определяются по формуле:

,

где x_max, x_min - максимальное и минимальное значения признака в совокупности.

При расчете интервала его величину округляют. Трехзначное, четырехзначное или большее число округляют до ближайшего числа кратного 50 или 100. Если число имеет два знака до запятой и несколько знаков после запятой, его округляют до целого, если один знак до запятой и несколько значений после запятой – до десятых и т.д.

Интервалы группировок могут быть закрытыми и открытыми. Закрытые интервалы имеют верхнюю и нижнюю границу. Открытые интервалы имеют только одну границу: верхнюю – первый, нижнюю – последний. Например, группы фирм по объему товарооборота (в тыс. руб.): до 50, 50-100, 100-500, 500 и более. Открытые интервалы используются обычно в тех случаях, когда признак в выделенной группе изменяется неравномерно и в широких пределах.

Если основанием группировки служит непрерывный признак, то одно и то же значение признака выступает и верхней и нижней границами смежных интервалов (например, группы магазинов по торговой площади (м²): 100-300, 300-500, 500-700, 700-900). При таком обозначении границ отнесение единицы совокупности, совпадающей по значению с границей интервала, к определенному интервалу можно проводить двояко: только к предыдущему интервалу, или только к последующему. В первом случае используется принцип «включительно» для верхней границы и «исключительно» для нижней; во втором - наоборот.

Если в основании группировки лежит дискретный признак, то нижняя граница i-го интервала равна верхней границе (i-1) интервала, увеличенной на 1. Например, группы фирм по числу персонала (чел.): 50-100, 101-150, 151-200, 201-250.

Для каждой группы определяются частоты. Частотами (f_i) называют численности отдельных вариантов или группы вариационного ряда, т.е. это числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения.

Частостями (w_i) называются частоты, представленные в относительном выражении (в долях единицы или в процентах):

Используются и другие характеристики рядов (численности). Если рассматривается вариационный ряд с неравными интервалами, то для правильного представления характера распределения рассчитывается абсолютная или относительная плотность распределения.

Накопленная частота показывает число единиц совокупности, у которых значение варианта не больше данного. Накопленная частота для данного варианта или верхней границы данного интервала получается суммированием (накапливанием) частот всех предшествующих интервалов, включая данный:

F_j = ∑f_i

Анализ рядов распределения можно наглядно проводить на основе их графического представления. Для этой цели строят полигон, гистограмму, огиву, кумуляту распределения.

Для графического изображения интервальных вариационных рядов используется гистограмма. На оси абсцисс откладываются величины интервалов и на этих отрезках, как на основаниях строят прямоугольники, высота которых пропорциональна частоте или частости. Для ряда с неравными интервалами по оси ординат откладывают плотности распределения, чтобы устранить влияние величины интервала (рис.1).

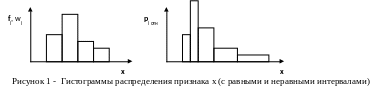
Для построения накопленных частот (частостей) на оси x откладывают варианты или верхние границы интервалов, а на оси у – соответствующие накопленные частоты (или частости). Можно построить кумулятивное распределение «меньше чем», а можно «больше чем».