Решение задач 5-6

Надо изучить теоретический материал (см. задачник [2], гл.7) по вопросам:

1) Понятие определенного интеграла. Геометрический смысл определенного интеграла.

2) Свойства определенного интеграла.

3)Формула Ньютона-Лейбница.

4) Подстановка и интегрирование по частям в определенном интеграле.

5) Вычисление площадей с помощью определенного интеграла.

Задача 5.

.

Задача 6. Изобразим в плоскости ХОУ фигуру, площадь которой требуется найти и вычислим ее площадь

Рекомендуемая литература

1. Виленкин, И. В. Высшая математика для студентов экономических, естественно-научных специальностей вузов : учеб. пособие / И. В. Виленкин, В. М. Гробер. – Ростов н/Д : Феникс, 2009.

2. Виленкин, И. В. Задачник по математике. Часть 1 / И. В. Виленкин, О. Е. Кудрявцев, М. М. Цвиль, И. С. Шабаршина. – Ростов н/Д : Российская таможенная академия, Ростовский филиал, 2007.

3. Вафодорова, Г.О. Математический анализ: курс лекций, Ч.1/ Российская таможенная академия. –М. :Изд-во Российской таможенной академии, 2014.-100с.

Часть II. «Дифференциальные уравнения и ряды»

Задача 7. Решить данные дифференциальных уравнений

1) ; 2) ;

3) ; 4) .

Решение задачи 7

Чтобы определить тип дифференциального уравнения первого порядка и решить его, надо изучить теоретический материал по вопросам:

1.1. Дифференциальные уравнения. Основные понятия.

1.2. Уравнения с разделяющимися переменными.

1.3. Однородные дифференциальные уравнения первого порядка.

1.4. Линейные уравнения первого порядка.

1.5. Уравнение Бернулли.

Теоретический материал и подробное решение типовых задач по этой теме можно найти в главе 12 учебника [4]; § 1-2 из [5] и в § 12 учебника [6].

1) Решить дифференциальное уравнение: . Это уравнение с разделяющимися переменными.

Преобразуем данное уравнение: ;

Разделим переменные:

.

Вычислим первый интеграл:

;

Таким образом, получаем:

.

2) Решить дифференциальное уравнение: .

Преобразуем исходное д.у., разделив обе его части на . Получим линейное неоднородное д.у. 1-го порядка : .

Разобьем решение этого уравнения на несколько этапов.

a) .

б)

.

Заметим, что при вычислении знак модуля мы просто опустили, так как согласно общей методике достаточно иметь одну функцию , обращающую в нуль квадратные скобки.

в) .

К полученному интегралу применим формулу интегрирования по частям:

.

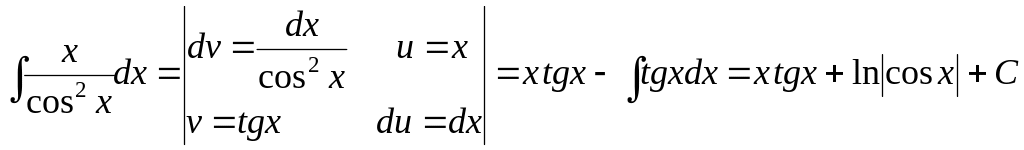Таким образом получаем: .

г) Общее решение имеет вид: .

6) Решить дифференциальное уравнение: .

Приведем данное д.у. к виду : .

а) .

б)

.

в)

.

г) — это общее решение данного д.у.

Рекомендуемая литература

4. Кремер, Н. Ш. Высшая математика для экономистов : учебник / Н. Ш. Кре-мер, Б. А. Путко, И. М. Фридман. – М.: Банки и биржи, ЮНИТИ, 2010.

5. Виленкин И.В. Практические указания по курсу «Математика» ( раздел «Дифференциальные уравнения»).– Ростов н/Д. РИО Ростов. ф. РТА, 1998.

6. Ермаков, В. И. Общий курс высшей математики для экономистов: учебник / В. И. Ермаков, Б. М. Рудык. – М.: ИНФРА-М, 2008.

Чтобы решить данные линейные дифференциальных уравнений второго порядка с постоянными коэффициентами:

3) ; 4) ;

вначале надо изучить теоретический материал по вопросам:

2.1. Основные понятия.

2.2. Линейные однородные дифференциальные уравнения второго по- рядка с постоянными коэффициентами, их общее решение.

2.3. Линейные неоднородные дифференциальные уравнения второго

порядка со специальной правой частью, их общее решение.

Теоретический материал и подробное решение типовых задач по этой теме можно найти в главе 12 учебника [4]; § 1-2 из [5] и в § 12 учебника [6].

Приведем решение одного из данных уравнений.

3) Решить дифференциальное уравнение: .

а) Записываем характеристическое уравнение, решаем его и находим :

.

б) Частное решение исходного неоднородного уравнения имеет вид: , где — неизвестный коэффициент. Подставив в исходное уравнение, найдем .

-25
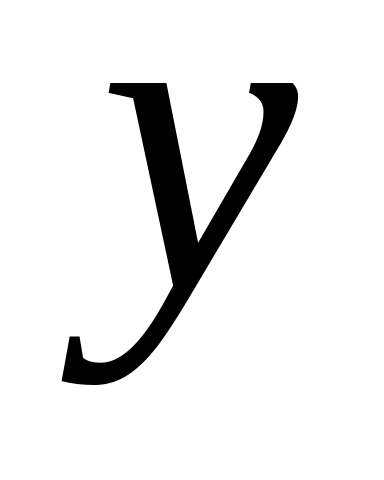
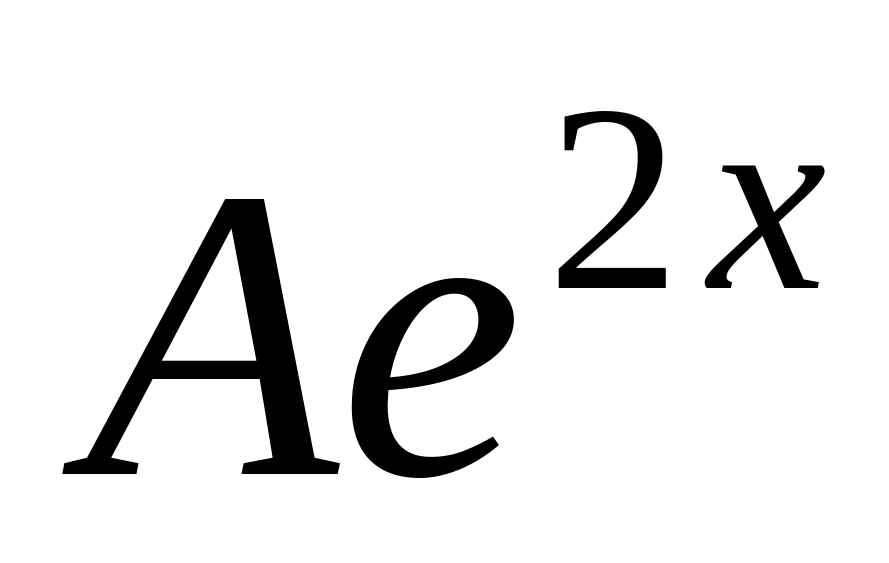
0
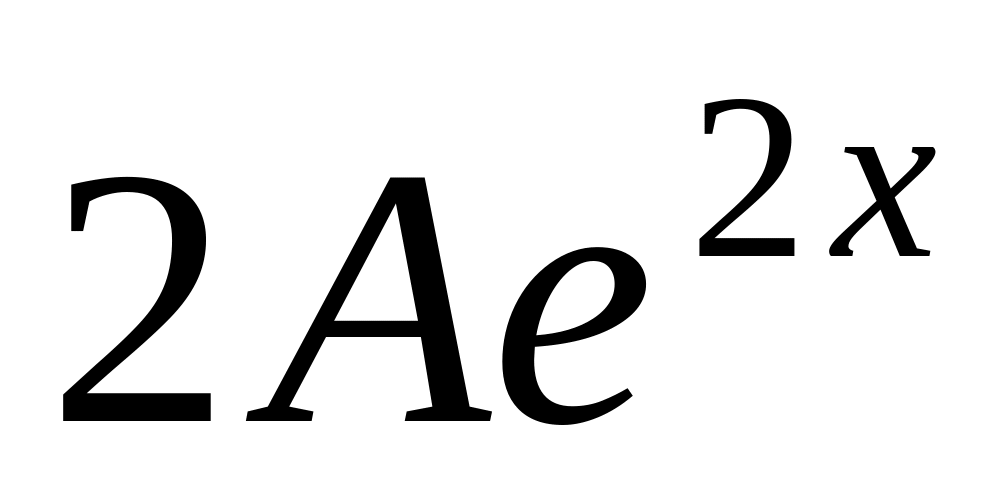
1

.

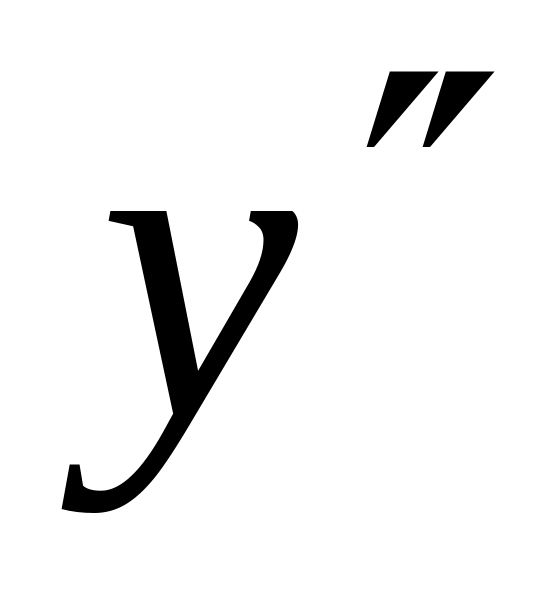
Итак, .

в) Руководствуясь формулой y_он y_чн , получаем:

.

4) Решить дифференциальное уравнение: .

а) Характеристическое уравнение имеет вид:

, .

б) Частное решение данного уравнения будем искать в следующем виде: . Подставляя в исходное уравнение, получим:

;

.

Приравняем слева и справа коэффициенты при одинаковых степенях :

Таким образом, получаем: .

в) Итак, .

Рекомендуемая литература

4. Кремер, Н. Ш. Высшая математика для экономистов : учебник / Н. Ш. Кре-мер, Б. А. Путко, И. М. Фридман. – М.: Банки и биржи, ЮНИТИ, 2010.

5.Виленкин И.В. Практические указания по курсу «Математика» ( раздел «Дифференциальные уравнения»).– Ростов н/Д. РИО Ростов. ф. РТА, 1998.

6. Ермаков, В. И. Общий курс высшей математики для экономистов: учебник / В. И. Ермаков, Б. М. Рудык. – М.: ИНФРА-М, 2008.

Задача 8. Исследовать на сходимость следующие ряды:

1) .	2) .	3)
4) . 5)