1.2 Геометрическая интерпретация и графическое решение задачи линейного программирования

Графический способ решения задач линейного программирования целесообразно использовать для решения задач:

– с двумя переменными, когда ограничения выражены неравенствами;

– со многими переменными при условии, что их можно свести к задачам с двумя переменными.

Пусть задача линейного программирования имеет следующий вид:

(1.21)

(1.22)

Каждое из неравенств (1.22) системы ограничений с геометрической точки зрения определяет на плоскости X₁OX₂ полуплоскость, ограниченную прямой .

Поскольку полуплоскость является выпуклым множеством, а пересечение конечного числа выпуклых множеств также выпукло, то область допустимых решений Ω задачи ЛП является выпуклым множеством. Если же это множество ограничено, то оно называется многоугольником решений.

Приведем несколько примеров областей допустимых решений задачи ЛП (рисунок 1.1).

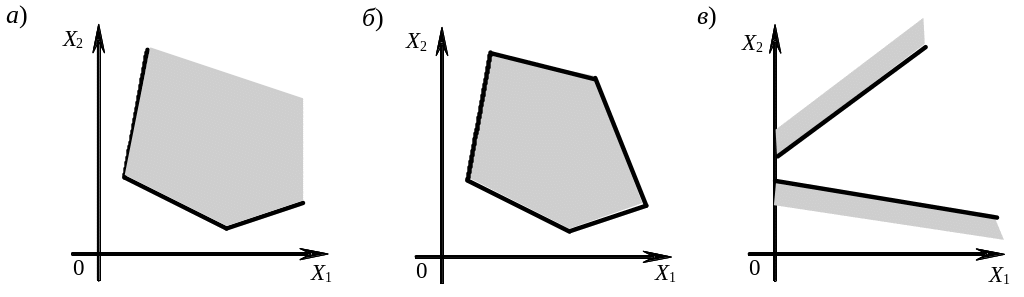
Рисунок 1.1 – Схемы различных областей допустимых решений:

a – неограниченная область; б – выпуклый многоугольник; в – пустое множество

Целевая функция (1.21) определяет на плоскости семейство параллельных прямых, называемых линиями уровня целевой функции, каждой из которых соответствует определенное значение целевой функции z. Найдем частные производные целевой функции по

Вектор – это вектор наискорейшего возрастания целевой функции, вектор градиентного направления. Направление, противоположное направлению вектора : , есть направление наискорейшего убывания целевой функции или антиградиентное.

Графический метод решения задачи линейного программирования состоит в следующем. Выбираем произвольное положение линии уровня целевой функции z, например, z = 0. Перемещаем прямую z = 0 в направлении вектора . При некотором значении z эта прямая впервые коснется области допустимых решений Ω. В данной точке (или точках) целевая функция достигает минимума. При дальнейшем перемещении прямой z по направлению вектора она коснется области допустимых решений Ω в последней точке (или точках). В данной точке (точках) целевая функция достигает максимума. Если же область Ω не ограничена, то сколько бы прямую ни перемещали в направлении вектора , она будет иметь общие точки с областью решений Ω. В этом случае целевая функция не ограничена.

Алгоритм графического решения задачи ЛП в случае двух переменных:

Шаг 1 Построить область допустимых решений Ω с учетом системы ограничений (1.22).

Шаг 2 Построить вектор наискорейшего возрастания целевой функции – вектор градиентного направления.

Шаг 3 Провести произвольную линию уровня целевой функции z=const, перпендикулярную к вектору .

Шаг 4 При решении задачи на максимум перемещать прямую z=const в направлении вектора , пока она не коснется области допустимых решений Ω в последней точке. В случае решения задачи на минимум линию уровня целевой функции z=const перемещать в антиградиентном направлении до последней точки касания с областью допустимых решений Ω.

Шаг 5 Определить оптимальный план . Возможны следующие случаи:

а) оптимальный план единственный. Тогда линия уровня и область допустимых решений Ω в крайнем положении будут иметь одну общую точку (рисунок 1.2: a – на mах и min, б – на min);

б) оптимальных планов может быть бесконечное множество. В этом случае в крайнем положении линия уровня проходит через грань области Ω (рисунок 1.2: б – на mах, в – на min);

в) целевая функция не ограничена. Линия уровня, сколько бы ее ни перемещали, будет иметь общие точки с областью допустимых решений Ω (рисунок 1.2: в – на mах, г – на mах и min);

г) задача решения не имеет. Область допустимых решений – пустое множество, т. е. система ограничений (1.17) несовместна (рисунок 1.2, д).

Шаг 6 Вычислить значение целевой функции по формуле (1.16).

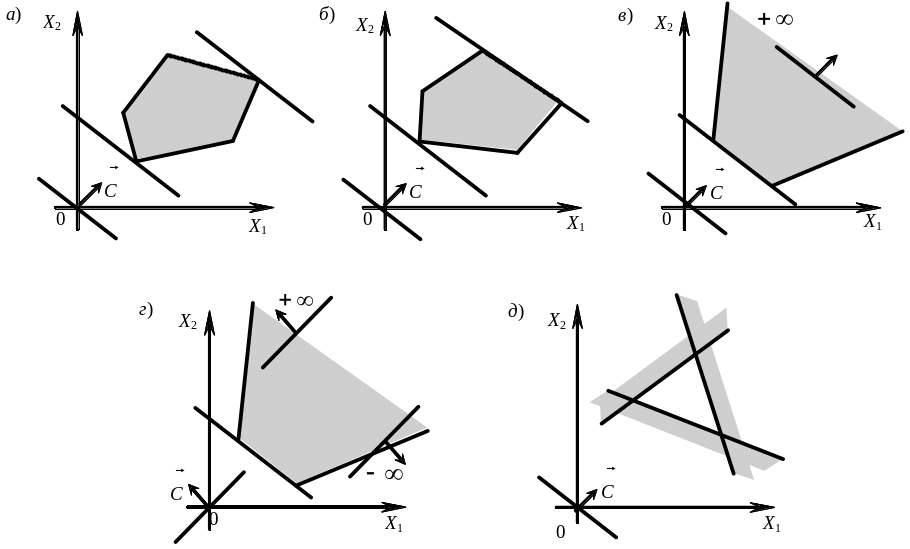
Рисунок 1.2 – Варианты ситуаций при решении задач ЛП графическим методом

Рассмотрим пример решения задачи линейного программирования графическим методом.

Пример 1.1.

z = x₁ + 2 x₂  max (min)

3 x₁ – x₂ ≥ 8

– x₁ + 3 x₂ ≤ 16

2 x₁ – x₂ ≤ 13

x₁ + 4 x₂ ≥ 20

x₁ ≥ 0; x₂ ≥ 0

С учетом системы ограничений построим множество допустимых решений Ω (рисунок 1.3).

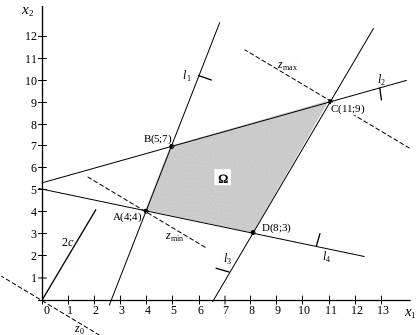
Рисунок 1.3 – Графическое решение задачи

Строим в системе координат x₁Ox₂ прямые :

l₁ : 3 x₁ – x₂ = 8;

l₂ : – x₁ + 3 x₂ = 16;

l₃ : 2 x₁ – x₂ = 13;

l₄ : x₁ + 4 x₂ = 20.

Изобразим полуплоскости, определяемые системой ограничений. Находим множество допустимых решений Ω как общую часть полученных полуплоскостей – четырехугольник АВСD.

Строим вектор градиентного направления (1; 2). Для большей наглядности построим вектор 2 = (2; 4)

Строим произвольную линию уровня целевой функции, например z = 0, перпендикулярную к вектору . Перемещаем прямую z = 0 в направлении вектора до последней точки ее пересечения с областью допустимых решений Ω. В точке С целевая функция достигает максимума. Находим координаты точки С – точки пересечения прямых l₂ и l₃ как решение системы уравнений:

Следовательно, Х^* = (11; 9).

Вычислим значение целевой функции z_mах = z (Х^*) = 11 + 29 = 29.

Перемещаем эту прямую z = 0 в антиградиентном направлении до последней точки ее пересечения с областью допустимых решений Ω. В точке А целевая функция достигает минимума. Находим координаты точки А – точки пересечения прямых l₁ и l₄ как решение системы уравнений:

Следовательно, Х^* = (4; 4).

Вычислим значение целевой функции z_min = z (Х^*) = 4 + 24 = 12.