Лабораторна робота №6 Виробнича регресія Кобба-Дугласа

ЗАВДАННЯ

Припустимо, що обсяг випуску продукції має вигляд

, (6.1)

де Y – обсяг випущеної продукції, X₁ – працезатрати, X₂ – основні засоби розглянутої галузі.

На основі статистичних даних, які надані у таблиці 5, використовуючи метод найменших квадратів, знайти:

1) оцінки параметрів виробничої регресії a₀, a₁, a₂;

2) з надійністю Р=0,95 встановити адекватність прийнятої математичної моделі статистичним даним. Якщо модель адекватна статистичним даним, то знайти значення прогнозу Y_p та його надійний інтервал;

3) побудувати ізокванту Y=с, де с – одне із значень планового обсягу випуску продукції;

4) використовуючи розрахунки, зробити висновки.

Таблиця 5 – Статистичні дані

X1	50	60	70	80	90	100	110	120	130	140	150
X2	90	100	110	120	130	140	150	160	170	180	190
Y	152	172	192	213	232	253	275	293	314	334	354

ХІД РОБОТИ

Припустимо, що між показником Y – обсягом випущеної продукції і факторами X₁ – працезатратами, X₂ – обсягом основних засобів існує стохастична залежність: (виробнича регресія Кобба-Дугласа).

Для оцінки параметрів виробничої регресії приводимо її до лінійної форми шляхом логарифмування обох частин рівняння:

. (6.2)

Після логарифмування і заміни змінних Y₁=ln(Y), Z₁=ln(X₁), Z₂=ln(X₂) отримаємо приведену лінійну регресію Y₁=a₀+a₁Z₁+a₂Z₂, де a₀=ln(a_o). Для розв’язування задачі складаємо електронну таблицю в Excel.

Вихідні дані розміщуються в блоці A3:C13. Значення факторів для прогнозу – в клітинках A14, B14. Перетворені змінні Z₁=ln(X₁), Z₂=ln(X₂), Y₁=ln(Y) розміщуються відповідно в блоках: D3:D14, E3:E14, F3:F13. Для обчислення значень у цих блоках використовуємо вбудовану математичну функцію Ln. Перетворені значення використовуємо для складання системи нормальних рівнянь.

У 15-му рядку знаходимо значення суми відповідного стовпчика.

Для обчислення коефіцієнтів при невідомих a₀, a₁, a₂ і вільних членів, зручно використовувати електронні таблиці. Скористуємося системою рівнянь, яка має вигляд ZA=T. Запишемо матрицю коефіцієнтів системи Z в діапазоні А18:С20. Вона складається наступним чином:

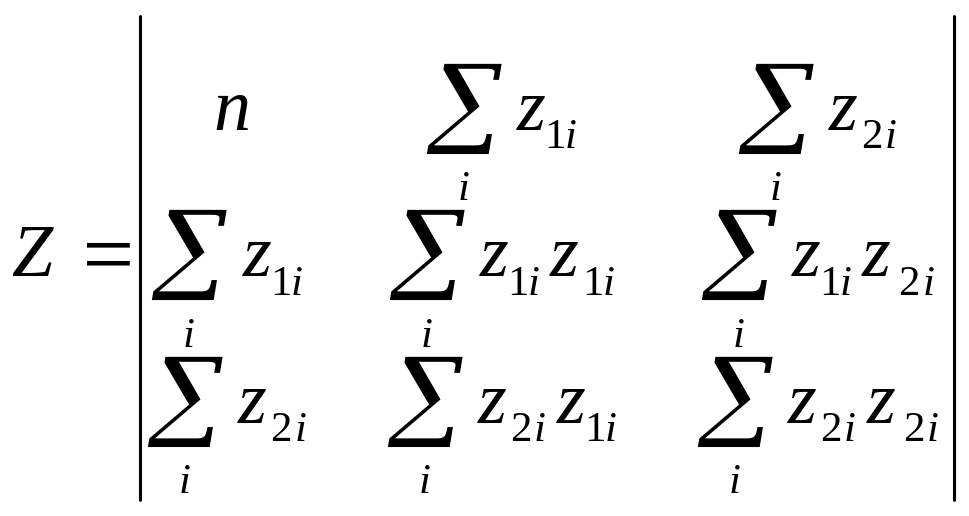(6.3)

Значення типу суми добутків параметрів визначаємо за допомогою функції (=СУММПРОИЗВ(D3:D13;E3:E13)).

Визначаємо обернену матрицю Z^-1 в діапазоні А23:С25 за допомогою функції МОБР( ). Застосовуємо комбінацію клавіш Ctrl+Shift+Enter для отримання значень матриці. Знаходимо вектор вільних членів Т в діапазоні Е18:Е20. Значеннями вектору є:

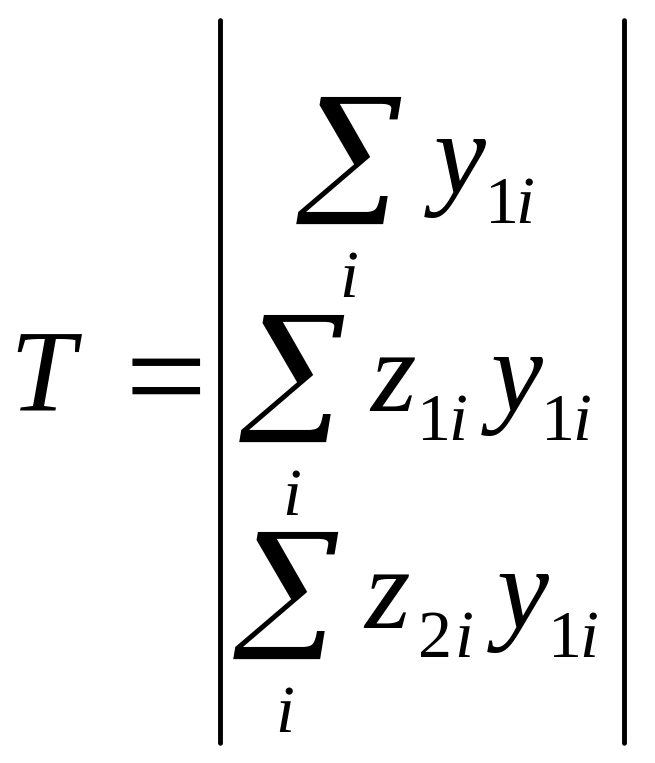(6.4)

Для визначення суми добутків використовуємо функцію, як і в попередньому випадку формування матриці Z.

Застосувавши функцію МУМНОЖ для значень оберненої матриці Z^-1 та вектору вільних членів Т, визначаємо параметри а₀, а₁, а у діапазоні Е23:Е25.

У блоці G3:G14 за формулою Y₁=a₀+a₁Z₁+a₂Z₂ обчислюємо значення показника приведеної лінійної регресії. У блоці H3:H14 з використанням вбудованої математичної функції EXP та отриманих значень блоку G3:G14 знаходяться розрахункові базисні та прогнозні значення показника.

Для визначення адекватності вибраної математичної моделі експериментальним даним визначимо оцінку тісноти та значимості зв’язку змінних у регресійній моделі. Під терміном «значимість зв’язку» (істотність, або значущість) розуміють оцінку відхилення вибіркових змінних від своїх значень у генеральній сукупності спостережень за допомогою статистичних критеріїв. У поняття «тіснота зв’язку» (щільність) вкладається оцінка впливу незалежної змінної на залежну змінну. Для цього обчислюємо значення квадратів відхилень фактичних значень показника від розрахункових та середніх значень показника у блоці I3:K13. Для обчислення середніх значень блоку C3:C13 використовуємо вбудовану статистичну функцію СРЗНАЧ(блок) – середнє статистичне значення блоку. Результат розрахунку розташовано у комірці H18.

Коефіцієнт кореляції та розрахункове значення критерію Фішера обчислюється у клітинках G19, G20 відповідно.

Для характеристики значимості зв’язку розрахуємо коефіцієнт кореляції R за формулою (1.4) даних методичних вказівок. Чим ближче коефіцієнт кореляції до одиниці, тим істотніше зв’язок між незалежною та залежними змінними.

Розрахункове значення критерію Фішера Fр обчислюється у клітинці K18 за формулою (1.5). Критичне (табличне) значення критерію Фішера розраховується у клітинці K19 за допомогою статистичної функції FРАСПОБР( ) з імовірністю 0,05 та степенями вільності k₁=m та k₂=n-m-1.

Значення S² дорівнює та обчислюється у клітинці N18.

Табличне (критичне) значення критерію Стьюдента T_кр розраховується в клітинці N19 за допомогою статистичної функції СТЬЮДРАСПОБР( ), з імовірністю 0,05 та степеню вільності k₁=n-m-1.

Для обчислення довірчого інтервалу оцінки прогнозного значення спочатку обчислюємо у комірках D28:F28 добуток вектора прогнозних значень та оберненої матриці , використовуючи вбудовану функцію {=МУМНОЖ($C$14:$E$14;A23:C25)}, а потім визначаємо скалярний добуток отриманого вектору та вектора прогнозних значень у клітинці E30 за допомогою статистичної фуккції (СУММПРОИЗВ(блок1:блок2)). Вектор Z_p знаходиться у рядку C14:E14, а матриця – в блоці A23:C25, причому в блоці для рядка Z_p вказуються абсолютні адреси, а для матриці – відносні адреси.

Значення DY₁ розраховується у клітинці E32 за формулою:

(6.5)

Значення Y_1p-DY₁ (=G14-E32), Y_1p+DY₁ (=G14+E32) обчислюються відповідно в клітинках I29:I30.

У клітинках L29:L30 з використанням вбудованої математичної функції EXP та значень клітинок I29:I30 знаходимо Y_p-DY₁ та Y_p+DY₁.

Для більш повного уявлення взаємозамінності факторів виробничої регресії розглянемо її ізокванти. Для регресії, що розглядається, геометричне місце точок факторів X₁, X₂ (різні комбінації факторів), для яких показник Y залишається сталим, називається ізоквaнтою. Виявимо комбінацію факторів, при яких буде виконано плановий обсяг випуску продукції Y₀, тобто знайдемо рівняння ізокванти. Щоб побудувати її, необхідно виразити один із факторів виробничої регресії через інший фактор і стале значення показника регресії:

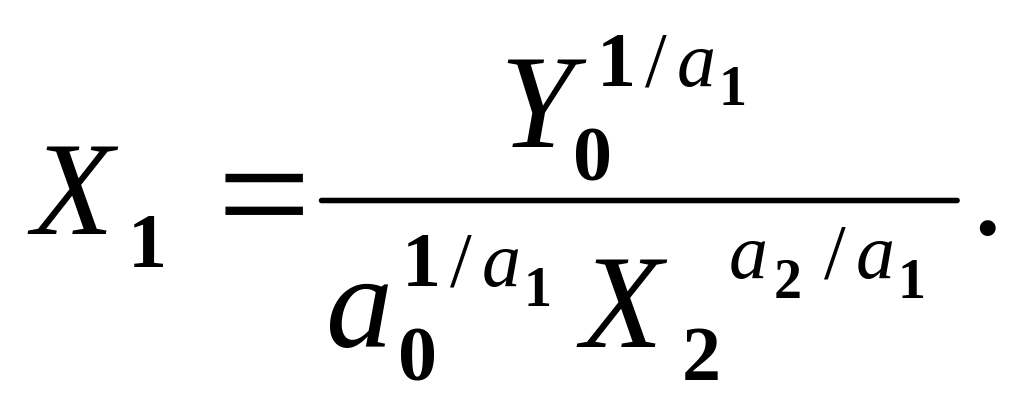(6.6)

Якщо сталу 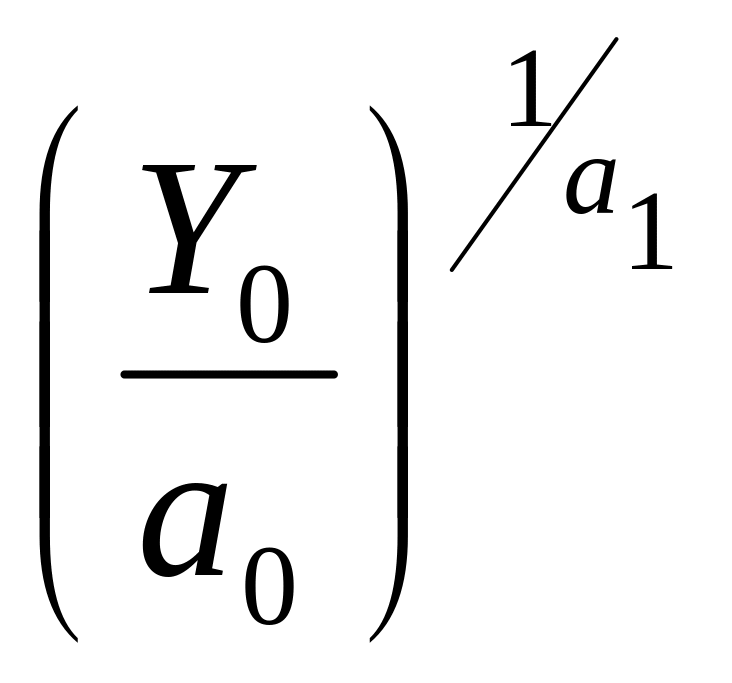позначити за b, то отримаємо залежність 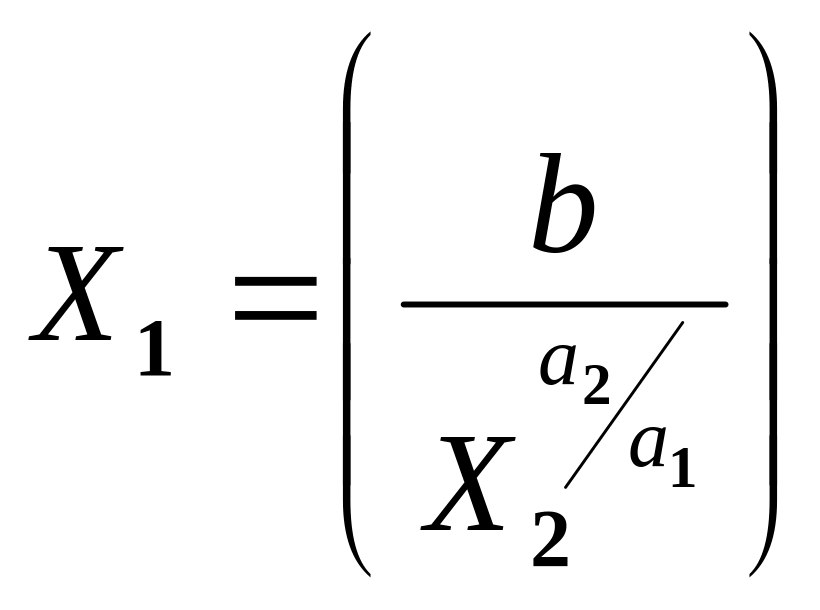. Спочатку у клітинці B34 за допомогою ЕХР знаходимо значення a₀ (=EXP(E23)), а потім значення оцінки параметра визначається в клітинці B35: .

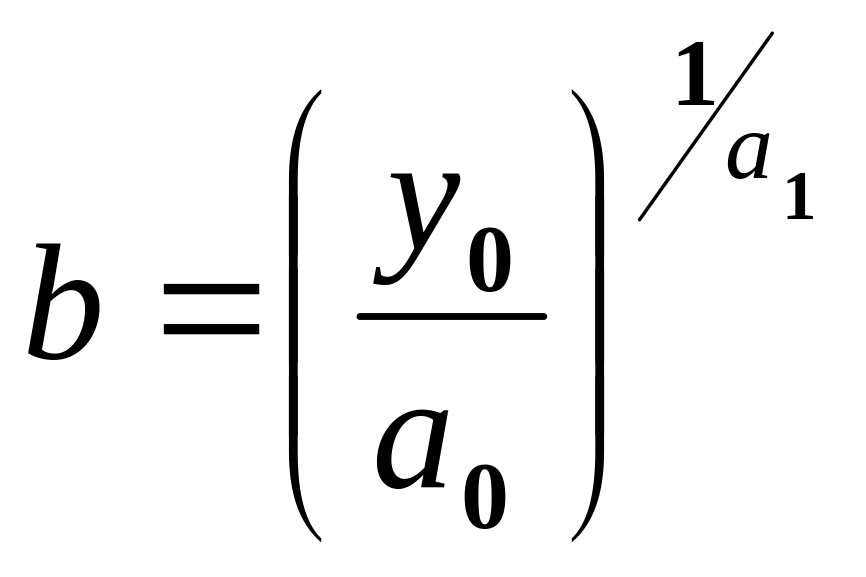Змінна Y_i залежно від основних засобів X₂ (C40:C50) дорівнює (B3:B13), працезатрати X₁ (E40:E50) обчислюються за формулою 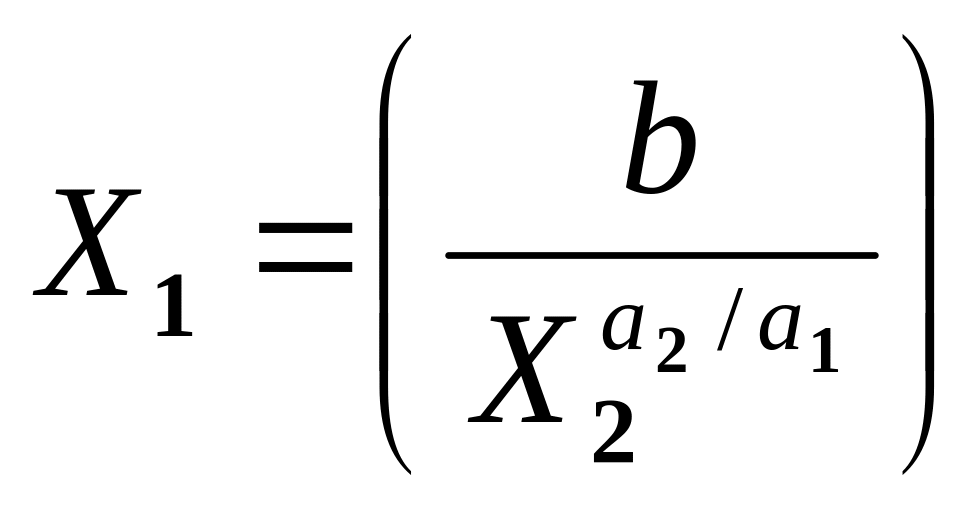. Використовуючи Мастер диаграмм, будуємо графік ізокванти.

Результати виконаних розрахунків можна побачити на рисунку 6.

ВИСНОВКИ

1. Знайдена математична модель 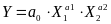з коефіцієнтами a₀= 0,508; a₁= 0,219; a₂= 0,813.

2. Оскільки F_роз=4001,69 > F_кр=4,459, то з надійністю Р=0,95 можна вважати, що прийнята математична модель адекватна експериментальним даним та її можна застосувати для аналізу господарської діяльності підприємства.

3. Параметри a₁=0.219 і a₂=0.813 є частинними коефіцієнтами еластичності, тобто зміна фактора X₁ (працезатрати) на 1% при незмінному факторі X₂ (основні засоби) викликає зміну обсягу випуску продукції на 0.219%, аналогічно зміна фактора X₂ на 1% при незмінному факторі X₁ викликає зміну обсягу випуску продукції на 0.813%.

4. Темпи приросту показника виражаються лінійно через темпи приросту факторів: 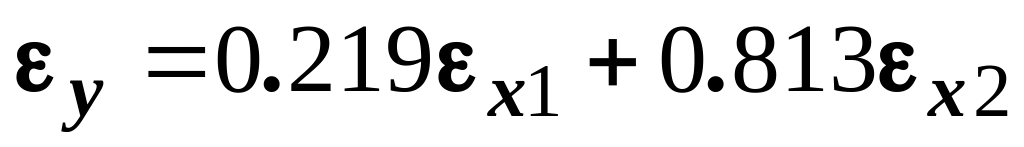, де – темпи приросту показника і факторів відповідно.

5. Для факторів X₁=160, X₂=200 визначена оцінка прогнозу Y_p =374.79 і з надійністю Р=0,95 вона буде належати інтервалу (371.57;378.05).

6. Оскільки сумарний коефіцієнт еластичності А=а₁+а₂=1.032, то при збільшенні обсягу основних засобів та обсягу працезатрат у k разів обсяг випуску продукції збільшиться у k^1.032 разів.

Рисунок 6 – Вікно розрахункових даних