Лабораторна робота №5 Множинна лінійна регресія (частина 2) Побудова лінії регресії

ЗАВДАННЯ

Допустимо, що між показником Y і факторами Х₁, Х₂ існує лінійна залежність:

(5.1)

Використовуючи пакет електронних таблиць Excel зробити наступну роботу:

1. Знайти оцінки параметрів а₀, а₁, а₂ .

2. За критерієм 2 перевірити мультиколінеарність усього масиву факторів.

3. Використовуючи критерій Фішера, з надійністю P=0,95 перевірити статистичну гіпотезу про адекватність прийнятої економічної моделі статистичним даним.

4. Якщо модель адекватна статистичним даним, то знайти прогноз показника Y_p та його надійний інтервал.

5. Якщо модель адекватна статистичним даним, то знайти коефіцієнт еластичності К_ел для базисних даних і прогнозу.

6. Побудувати графіки статистичних даних та лінії регресії.

7. На основі одержаної економетричної моделі зробити висновки.

ХІД РОБОТИ

Знайдемо оцінки параметрів, використовуючи матричні операції. Запишемо систему нормальних рівнянь у матричній формі.

(5.2)

Якщо помножити матричне рівняння зліва на матрицю то для оцінки параметрів вектора отримаємо формулу:

(5.3)

Крок 1. Знаходження оцінок параметрів регресії.

1. Знаходимо в блоці А39:О41 транспоновану матрицю [X]^T по відношенню до матриці вхідних даних [X] в блоці АЗ:С17, використовуючи в категорії «Ссылки и массивы» вбудовану функцію ТРАНСП (А3:С17).

2. Знаходимо кореляційну матрицю, як добуток матриць [X]^T та [X] в блоці А45:С47, використовуючи вбудовану математичну функцію МУМНОЖ (блок даних першої матриці А39:041; блок даних другої матриці АЗ:С17).

3. Знаходимо обернену матрицю Z*= до кореляційної в блоці Е45:G47, використовуючи вбудовану математичну функцію МОБР( ).

4. Визначаємо добуток матриць [X]^T та Y в блоці I45:I47, використовуючи вбудовану математичну функцію МУМНОЖ( ).

5. Застосувавши вбудовану математичну функцію МУМНОЖ для отриманих на попередньому кроці матриць та [X]^TY, знаходимо оцінки вектора (параметри а₀, а₁, а₂). Отримані рішення знаходяться в блоці K45:K47.

Крок 2. Перевірка мультиколінеарності масиву двох факторів за критерієм 2 .

1. Знаходимо транспоновану матрицю [X*]^T в блоці А50:О51 по відношенню до матриці вхідних даних [X*] в блоці FЗ:G17, використовуючи в категорії «Ссылки и массивы» вбудовану функцію ТРАНСП ( ).

2. Знаходимо кореляційну матрицю R*, як добуток матриць [X*]^T та [X*] в блоці А54:B55, використовуючи вбудовану математичну функцію МУМНОЖ().

Знаходимо детермінант (визначник) кореляційної матриці |R*|. Для цього в комірці D55 запишемо визначник кореляційної матриці det[Kor*] за допомогою функції МОПРЕД( ).

Для перевірки наявності мультиколеніарності між змінними Х₁ та Х₂ визначаємо розрахункове та табличне значення критерію ². Розрахункове значення визначаємо в комірці F55 за формулою (4.3) попередньої роботи. Знаходимо табличне значення ²_і при заданому рівні значущості =0.05 і ступені вільності k = ½ m(m – 1). Розрахунок виконується в комірці G55 за формулою .

Порівнюючи ²_роз> ²_табл за абсолютною величиною, можна побачити, що в нашому випадку в масиві факторів не існує мультиколінеарності.

Крок 3. Перевірка статистичної гіпотези про адекватність прийнятої економічної моделі статистичним даним.

Оцінки параметрів регресії можна знайти, використовуючи вбудовану статистичну функцію ЛИНЕЙН.

Опишемо порядок знаходження оцінок параметрів регресії з використанням функції ЛИНЕЙН:

1.  Відмічаємо блок, де мають знаходитись розрахункові дані А59:С63, ширина блоку дорівнює числу оцінюваних параметрів, а висота дорівнює п’яти рядкам.

2.  Вибираємо функцію ЛИНЕЙН у полі категорії СТАТИСТИЧЕСКИЕ. У діалоговому вікні вводимо: в перший рядок (в перше поле) блок даних показника Y, вказуючи діапазон комірок ЕЗ:Е17; у другий рядок – блок даних факторів Х₁, Х₂ (блок ВЗ:С17); в третій рядок вводиться слово ИСТИНА або 1, якщо а₀ не дорівнює нулю, і слово ЛОЖЬ або 0, якщо а₀ дорівнює нулю; в четвертий рядок вводиться слово ИСТИНА, якщо необхідно знайти не лише параметри лінії регресії, а й додаткову регресійну статистику. Якщо необхідно знайти лише параметри лінії регресії, то вводимо слово ЛОЖЬ і натискаємо на кнопку ГОТОВО для отримання розрахункових даних.

3.  Для того, щоб у блоці розрахункових даних було видно не лише значення першої комірки, підтверджуємо введення комбінацією клавіш Ctrl+Shift+Enter.

Опишемо розрахункові дані:

У першому рядку справа наліво знаходяться оцінки параметрів множинної лінійної регресії відповідно a₀, a₁, a₂.

У другому рядку справа наліво знаходяться середні квадратичні відхилення оцінок параметрів σ_a0, σ_α1, σ_α2 .

У третьому рядку в першій комірці знаходиться коефіцієнт детермінації, в другій комірці – середнє квадратичне відхилення показника.

У четвертому рядку в першій комірці знаходиться розрахункове значення F-статистики, в другій комірці знаходиться k – число ступенів вільності.

У п’ятому рядку в першій комірці знаходиться сума квадратів відхилень розрахункових значень показника від його середнього значення, в другій комірці – залишкова сума квадратів.

Таблиця розрахункових значень додаткової регресійної статистики має вигляд:

a2	a1	a0
σa2	σa1	σa0
r2	S	#Н/Д
Fr1	k	#Н/Д
		#Н/Д

Порівняємо розрахунки, отримані різними методами. Оцінки параметрів, отримані з використанням матричної алгебри і вбудованої статистичної функції ЛИНЕЙН, співпадають (блок K45:K47, блок А59:С59). Співпадають сума квадратів відхилень (комірки К19 та В63).

Середньоквадратичні відхилення параметрів знаходяться у блоці А60:С60. Розрахункове значення F-критерію знаходиться у комірці А62 та дорівнює 885.043, а критичне дорівнює 3,89. Оскільки F_розр.>F_крит., то з надійністю Ρ=0,95 можна вважати, що прийнята математична модель адекватна експериментальним даним.

Розглянемо значущість параметрів регресії. Для цього розрахуємо t-статистику кожного із параметрів за формулою

, (5.4)

де _i – оцінки параметрів множинної лінійної регресії;

_i – середні квадратичні відхилення оцінок параметрів. Значення _i запишемо у діапазоні E60:G60.

Розрахункові значення знаходяться у стовпці I60:K60.

Крок 4. Знайти прогноз показника Yp та його надійний інтервал.

Запишемо модель показника Y у діапазоні I3:I17. У стовпчику J3:J17 визначимо різницю між статистичними та розрахунковими даними та у стовпчику К3:К17 квадрат цієї різниці.

Точкову оцінку значення прогнозу для Х₁=9, Х₂=30 знаходимо у комірці I18. Довірчий інтервал цієї точкової оцінки знаходимо у стовпчику G68:G69 і обчислюємо за формулою:

де (5.5)

Розглянемо алгоритм розрахунку довірчого інтервалу прогнозу.

1. Використовуючи вбудовану математичну функцію МУМНОЖ (блок вектора 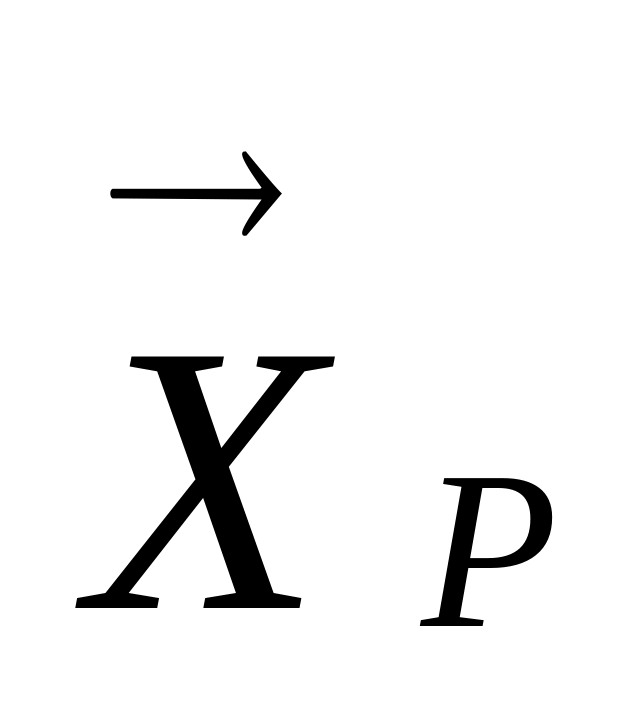– А18:С18, блок матриці Z – E45:G47), знаходимо добуток 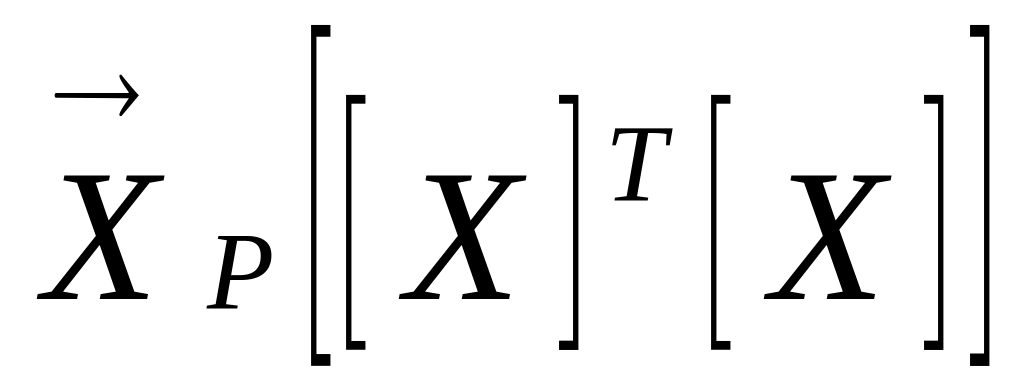(блок B66:D66).

2. Використовуючи вбудовану математичну функцію СУММПРОИЗВ(B66:D66;А18:С18), знаходимо в комірці G66 значення

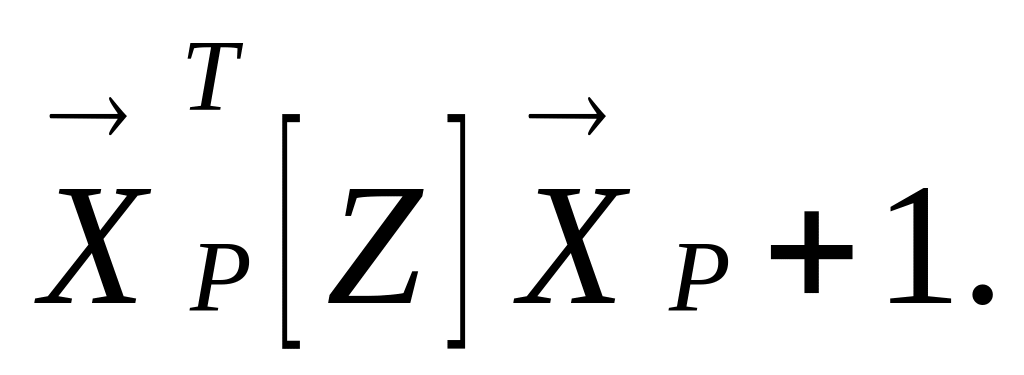
3. Використовуючи вбудовану математичну функцію КОРЕНЬ, знаходимо в комірці C68 значення S_yp, а потім у комірці C69 – t·S_yp .

4. Довірчі межі прогнозу знаходимо в блоці G68:G69.

Крок 5. Коефіцієнт еластичності К_ел для базисних даних і прогнозу.

Частинні коефіцієнти еластичності для прогнозу знаходимо за формулами , у комірках, відповідно, J68 та J69.

Результати виконаних розрахунків можна побачити на рисунку 5.

Рисунок 5 – Вікно розрахункових даних

Висновки

1. Між факторами Х₁ і Х₃ існує мультиколінеарність, тому один із факторів Х_З не включаємо в множинну лінійну регресію.

2. Оскільки F_розр>F_крит., то з надійністю Р=0,95 можна вважати математичну модель Y = 2,55+1,25X₁+1,99X₂ адекватною експериментальним даним. На основі цієї моделі можна робити економічні висновки.

3. З надійністю Р=0,95 можна вважати, що вплив факторів Х₁, Х₂ на показник Y значний.

4. Прогнозне значення показника з надійністю Р=0,95 буде знаходитись у проміжку (70.82; 76.52).

5. При зміні факторів у точці прогнозу Х_1Р на 1 % показник зміниться на 0,15% при незмінних значеннях фактора Х_2Р.

6. При зміні фактора у точці прогнозу Х_2Р на 1% показник зміниться на 0,81% при незмінних значеннях фактора Х_1Р.