Лабораторна робота №4 Множинна лінійна регресія (частина 1) Мультиколінеарність

ЗАВДАННЯ

Економічний показник Y залежить від трьох факторів. На основі статистичних даних за 15 періодів, які надані у таблиці 4, побудувати кореляційну матрицю.

Таблиця 4 – Статистичні дані

X1	3,82	4,33	4,82	5,23	5,77	5,92	6,53	6,57	7,47	7,56	7,97	8,3	8,54	8,77	8,9
X2	10,11	12,34	18,45	15,78	20,2	9,56	22,56	12,36	17,98	15,36	13,45	18,14	11,34	10,45	29,26
X3	23,2	24,49	26,8	28,09	30,3	31,97	33,93	35,22	36,19	36,87	38,99	40,75	41,41	42,96	43,98
Y	26,02	33,1	46,15	41,15	51,46	28,67	55,76	34,11	47,37	42,29	41	48,06	35,91	35,27	71,33

Використовуючи ²_і – критерій, з надійністю Р=0,95 оцінити наявність загальної мультиколінеарності, тобто наявності тісної лінійної залежності або сильної кореляції між двома чи більше факторами. Якщо існує загальна мультиколінеарність, потрібно, використовуючи t-статистику з надійністю Р=0.95, виявити пари факторів, між якими існує мультиколінеарність. Якщо такі пари існують, то один із факторів цієї пари виключити із розгляду.

ХІД РОБОТИ

В практиці економічні фактори часто пов’язані між собою і це істотно впливає на якість економетричного моделювання.

Основні наслідки мультиколінеарності:

1. Падає точність оцінок параметрів, яка виявляється в зростанні помилок деяких оцінок, в значному збільшені дисперсії оцінок параметрів.

2. Оцінки деяких параметрів стають незначущими.

3. Оцінки деяких параметрів стають чутливими до обсягів сукупності спостережень.

Тому при побудові економетричної моделі потрібно визначити існування мультиколінеарності та усунути її.

Значення змінних Х₁, Х₂, Х₃ запишемо в діапазоні B3:D17, а значення змінної Y в діапазоні Е3:Е17. В діапазоні А3:А17 запишемо значення допоміжної змінної Х₀, які дорівнюють 1. Умовно вважається, що вільний член а₀ рівняння регресії множиться на фіктивну змінну Х_i0, яка приймає значення 1 для всіх i. У 18 рядку визначаємо прогнозовані значення, а в 19 – суми значень відповідних змінних.

Для визначення мультиколінеарності застосовується алгоритм Фаррара – Глобера. Цей алгоритм використовує три види статистичних критеріїв.

За критерієм ² перевіряється мультиколінеарність усього масиву факторів.

За F–критерієм перевіряється незалежність кожного фактора з рештою факторів.

За критерієм Ст’юдента t перевіряється кожна пара незалежних факторів.

Алгоритм Фаррара – Глобера поділяється на декілька кроків.

Крок 1. Стандартизація (нормалізація) змінних факторів.

Матриця змінних факторів X замінюється стандартизованою матрицею X*, елементи якої обчислюють за формулами:

або (4.1.)

де n – число спостережень;

m – число пояснювальних змінних, (к=1,2,...,m);

– середнє арифметичне значень фактора Х_k;

δ²_xk – дисперсія (середнє квадратичне відхилення) k-ї пояснювальної змінної Х_k.

При нормалізації статистичних даних використовуємо статистичні функції СРЗНАЧ та СТАНДОТКЛОНП. Середнє значення факторів визначаємо в комірках B21, C21, D21, а середні відхилення в комірках I21, J21, K21. В комірці А21 визначаємо . Нормалізовані дані запишемо в діапазоні F3:H17. В комірці F3 запишемо формулу (=(B3-B$21)/$A$21/I$21), яку копіюємо в інші клітинки даного діапазону.

Крок 2. Знаходження кореляційної матриці стандартизованих факторів.

Кореляційна матриця R знаходиться відповідно до двох методів стандартизації факторів за формулами:

або (4.2.)

де X* – матриця стандартизованих незалежних змінних,

(X*)^T – матриця, транспонована до матриці X*.

В діапазоні А24:О26 запишемо транспоновану матрицю (X*)^T до матриці X* нормалізованих значень.

В діапазоні А29:С31 визначаємо кореляційну матрицю , для цього виділяємо цей діапазон, вибираємо математичну функцію МУМНОЖ та діапазони знаходження транспонованої матриці (X*)^T та матриці стандартизованих незалежних змінних X*. Ця функція повертає добуток матриць, які містяться в масивах. Результат – це масив з таким самим числом рядків, як і масив 1, та таким самим числом стовпців, як і масив 2. Для завершення операції використовуємо комбінацією клавіш Ctrl+Shift+Enter. Якщо вказані дії виконані правильно, то на головній діагоналі матриці розміщені 1.

Крок 3. Виявлення мультиколінеарності в масиві факторів.

Знаходимо детермінант (визначник) кореляційної матриці |R|. В комірці В34 запишемо визначник кореляційної матриці det[Kor] за допомогою функції (=МОПРЕД(A29:C31)).

Для перевірки наявності мультиколеніарності між змінними Х₁, Х₂, Х₃ визначаємо розрахункове та табличне значення критерію ². Розрахункове значення визначаємо в комірці D35 за формулою:

(4.3.)

Знаходимо табличне значення ²_і при заданому рівні значущості =0.05 і ступені вільності k = ½ m(m – 1)=3.

Розрахунок виконується в комірці E35 за формулою , яка у MS Excel має вигляд (=ХИ2ОБР(0,05;3)).

Якщо ²_роз > ²_табл, то в масиві факторів існує мультиколінеарність. В нашому випадку розрахункове значення за абсолютною величиною більше табличного, тому в масиві факторів існує мультиколеніарність. Отже один із факторів потрібно відкинути. Визначимо цей фактор.

Крок 4. Знаходження оберненої матриці до кореляційної матриці.

Обернену матрицю позначимо Z. Тоді

(4.4.)

В діапазоні E29:G31 за допомогою математичної функції (=МОБР(A29:C31)) визначимо обернену матрицю.

Крок 5. Перевірка мультиколінеарності фактора Х_к з іншими факторами.

Застосуємо критерії Фішера. Для цього знайдемо значення F статистики (F критерій Фішера) для кожного фактора за формулою:

(4.5.)

де z_kk – діагональний елемент матриці Z.

В таблиці критичних значень знаходимо значення F_табл при значущості =0,05 і ступенях вільності V₁= m-1 та V₂= n-m. Це значення становить 3.89.

Якщо F_факт> F_табл., то фактор X_k – мультиколінеарний з іншими факторами. В нашому випадку можна сказати, що перша та третя незалежні змінні мультиколінеарні:

Fфакт1	571,8679	>	3,89
Fфакт2	0,4087	<	3,89
Fфакт3	571,3672	>	3,89

Крок 6. Знаходження частинних коефіцієнтів кореляції

Використовуючи матрицю Z обчислюються частинні коефіцієнти кореляції за формулою

(4.6.)

де z_ij – елемент оберненої матриці Z, що міститься в i-ому рядку і в j- ому стовпчику,

z_ii та z_jj – діагональні елементи матриці Z.

В діапазоні І29:К31 запишемо матрицю Q, для цього вводимо в комірки даного діапазону формули згідно таблиці:

Ч астинні коефіцієнти кореляції характеризують тісноту зв’язку між двома змінними за умови, що третя не впливає на цей зв’язок.

Крок 7. Перевірка мультиколінеарності пари факторів.

Застосуємо критерій Ст’юдента. Для перевірки мультиколінеарності між факторами Х_k та Х_j обчислюють t-статистику за формулою

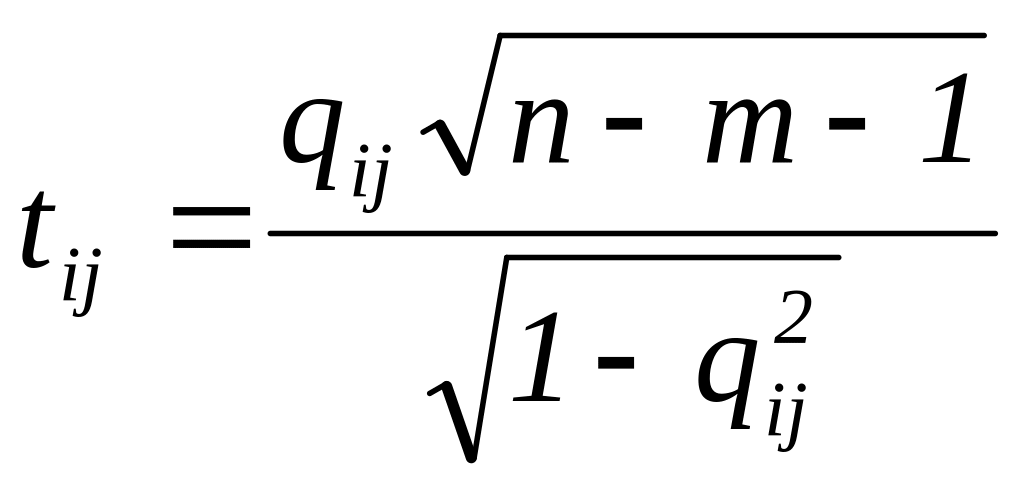(4.7.)

Отримані значення розміщуємо в діапазоні М29:О31. В комірці О34 запишемо значення критерію Ст’юдента, що відповідає імовірності 0,95 і кількості ступенів вільності k₁=n-m-1 за допомогою формули СТЬЮДРАСПОБР( ).

t12	0.098184	<	2.200985
t13	31.31886	>	2.200985
t23	-0.01	<	2.200985

В матриці Т елемент, що знаходиться в першому рядку та третьому стовпці, перевищує за абсолютною величиною табличне значення критерію Ст’юдента. Отже між факторами Х₁, Х₃ існує мультіколінеарність. Один із цих факторів потрібно відкинути. Відкидаємо фактор Х₃ і будуємо модель для факторів, які залишились. Результати виконаних розрахунків можна побачити на рисунку 4.

Р исунок 4 – Вікно розрахункових даних

ВИСНОВКИ

1. Порівнявши по модулю значення ²_роз=56,36 та ²_табл=7,81, виявили, що в масиві факторів існує мультиколінеарність.

2. Оскільки F-критерій в першому та третьому випадках більше ніж його табличне значення 571,87>3.89 та 571,37>3.89, то перша та третя незалежні змінні мультиколінеарні.

3. У першому випадку t₁₂=0,098 менше за табличне значення критерію Ст’юдента=2,2, то можемо стверджувати про відсутність мультиколеніарності між першою та другою змінною.

4. У другому випадку t₁₃=31,3 більше за табличне значення критерію Ст’юдента=2,2, можемо стверджувати про наявність мультиколеніарності між першою та третьою змінними.

5. У третьому випадку t₂₃=-0,01 менше за табличне значення критерію Ст’юдента=2,2, можемо стверджувати про відсутність мультиколеніарності між другою та третьою змінними.

6. Зважаючи на те, що між пояснювальними змінними досліджуваної моделі існує мультиколеніарність, що може привести до негативного впливу на кількісні оцінки параметрів економетричної моделі, потрібно позбутися мультиколеніарності, відкинувши одну зі змінних мультиколеніарної пари.