Лабораторна робота №3 Аналіз індивідуального ринку (регресія попиту)

ЗАВДАННЯ

На певний вид товару попит має вигляд, який надано у таблиці 3.

Таблиця 3 – Таблиця попиту товару

pi	1	2	3	4	5	6	7	8	9	10	11
di	8,15	7,24	6,31	6,24	5,47	4,53	3,67	3,08	2,44	1,81	1,45

де p_i – ціна в умовних грошових одиницях за одиницю товару;

d_i – кількість товару, проданого за певний період по ціні p_i.

На основі статистичних даних знайти оцінки параметрів регресії попиту, якщо вона має таку структуру:

.

Використовуючи критерій Фішера, з надійністю p=0,95 оцінити адекватність припущеної структури регресії статистичним даним. Якщо прийнята математична модель адекватна експериментальним даним, то для даного проміжку знайти:

• коефіцієнт еластичності для всіх значень цін;

• проміжки цін зростання та спадання товарообігу в грошовому вираженні;

• ціну на товар, за якої товарообіг у грошовому вираженні буде максимальним;

• проміжки цін зростання та спадання прибутку;

• оцінку ціни на товар, за якої прибуток буде максимальним, та його значення.

Потім побудувати графіки:

• статистичних даних та лінії регресії;

• товарообігу в грошовому вираженні для статистичних даних та для розрахункових значень;

• собівартості товару та прибутку залежно від обсягу випуску;

• лінії еластичності.

ХІД РОБОТИ

Вводиться гіпотеза, що між фактором p (ціна в умовних грошових одиницях за одиницю товару) та показником D (кількість товару, проданого за певний період по ціні p) існує стохастична залежність:

. (3.1)

Для розв’язання задачі складаємо електронну таблицю в Excel. Вхідні дані вводяться в діапазон A3:D13. У стовпцях C3:C13, D3:D13, Е3:Е13 обчислюються значення p_i², p_i³, p_i⁴ (i=1,...,11). Середній товарообіг у грошовому вираженні обчислюється у стовпчику F3:F13. Значення D·p_i² обраховуємо в діапазоні G3:G13. У 14 рядку знаходимо суму даних за стовпцями. Кількість спостережень визначаємо у комірці В18.

Для визначення параметрів а₀, а₁, а₂ моделі, скористуємося системою рівнянь, яка має вигляд ZA=T. Запишемо матрицю коефіцієнтів системи Z в діапазоні B23:D25. Вона складається наступним чином:

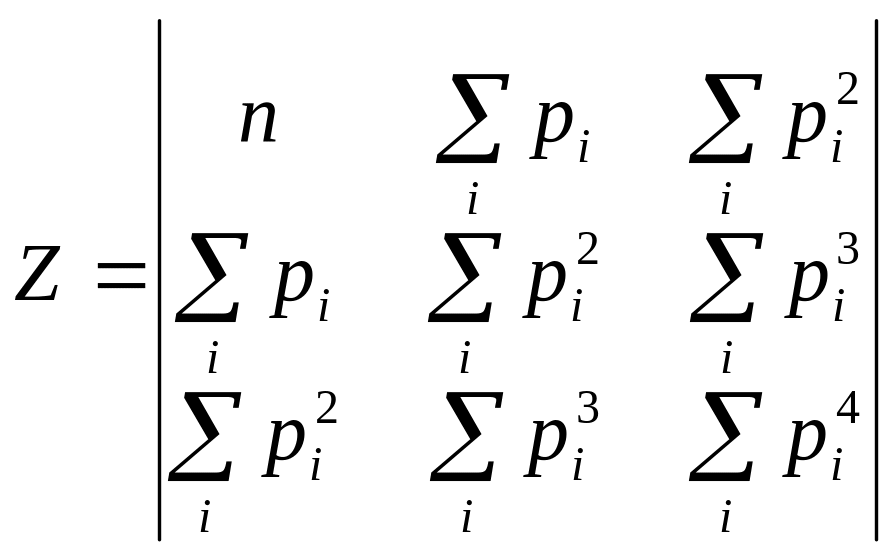(3.2)

Визначаємо обернену матрицю Z^-1 у діапазоні B28:D30. Для цього застосовуємо функцію МОБР категорії математичні функції, для даного діапазону. Задаємо діапазон коефіцієнтів системи Z і натискаємо комбінацію клавіш Ctrl+Shift+Enter. В результаті одержимо формулу =МОБР(B23:D25). Знаходимо вектор вільних членів Т в діапазоні G23:G25. Значеннями вектору є:

(3.3)

Застосувавши функцію МУМНОЖ для значень оберненої матриці Z^-1 та вектору вільних членів Т, визначаємо параметри а₀, а₁, а₂. Розрахункова формула має вигляд: (=МУМНОЖ(B28:D30;G23:G25)). Для більшої наочності значення параметрів запишемо у діапазоні B19:B21.

Розрахункове значення кількості проданого товару d_i по ціні p_i обчислюється в діапазоні Н3:Н13 за формулою (3.1).

Значення (D-Dr)² обчислюємо відповідно в діапазоні І3:І13. Для визначення квадрату відхилення значень кількості товару від середнього значення кількості товару у діапазоні J3:J13, можна визначити середнє значення D_c у комірці G18 та у розрахунковій формулі застосувати абсолютне посилання на дану комірку =(B3-$G$18)^2. Або одразу використати функцію =(B3-СРЗНАЧ($B$3:$B$13))^2.

Коефіцієнт еластичності для базисних значень та прогнозу обчислюється в діапазоні K3:K13 за формулою:

(3.4)

Визначаємо похідну . Отже, коефіцієнт еластичності дорівнює .

Визначимо коефіцієнт кореляції та розрахунковий коефіцієнт Фішера за формулами (1.4) та (1.5) із попередньої роботи. Результати запишемо у комірки G19 та G20 відповідно.

Табличне значення F-критерію для ймовірності p=0,95 і числа ступенів вільності k₁=m, k₂=n-m-1 визначаємо в комірці G21 за допомогою статистичної функції FРАСПОБР.

В комірках J16 та J17 запишемо постійні та змінні затрати. В діапазонах L3:L13 знаходимо товарообіг p·Dr, в M3:M13 – загальні затрати, в N3:N13 – прибуток.

Д ля визначення максимального значення товарообігу потрібно обрахувати похідну для рівняння товарообігу, прирівняти її до 0 та вирішити квадратне рівняння.

Значення дискримінанту рівняння визначається як:

(3.5)

Знайдемо корені рівняння за формулою:

(3.6)

Дискримінант D та корені рівняння p₁ та p₂ для визначення максимального товарообігу занесемо в комірки J20, J18, J19.

Значення прибутку визначається як різниця між загальними постійними та змінними витратами: .

Для визначення максимального прибутку потрібно обрахувати похідну для рівняння прибутку, прирівняти її до 0 та вирішити квадратне рівняння.

Значення дискримінанту рівняння визначається, як:

(3.7)

Знайдемо корені рівняння за формулою:

(3.8)

Дискримінант D₁ та корені рівняння p₃ та p₄ для визначення максимального прибутку занесемо в комірки J21, J22, J23.

Для наочності будуємо графічні зображення: статистичні дані та теоретичний попит, собівартість товару та прибутку в залежності від обсягу випуску, лінії еластичності, товарообігу в грошовому вираженні для статистичних та розрахункових значень.

Результати виконаних розрахунків можна побачити на рисунку 3.

Рисунок 3 – Вікно розрахункових даних

ВИСНОВКИ

1. Математична модель має вигляд: , a₀=8,853; a₁=-0,766; a₂=0,007.

2. Оскільки F_роз=538,09>F_таб=4,459, то з надійністю Р=0,95 можна вважати, що прийнята економетрична модель відповідає експериментальним даним і її можна використовувати для економічного аналізу.

3. Оцінка максимального товарообігу в грошовому виразі відповідає ціні p₂=6,33 у. г. од. і дорівнює 27,13 у. г. од. при обсязі товару D_r(p₂)=4,285.

4. Оцінка максимального прибутку відповідає ціні p₄=7,4 у. г. од. і дорівнює p*D_r-V(p₄)=9,28 у. г. од. при обсязі товару D_r(p₄)=3,57.

5. Максимальне значення оцінки товарообігу в грошовому виразі та максимальне значення прибутку досягаються при різних значеннях цін.