Лабораторна робота №2 Нелінійна парна регресія

ЗАВДАННЯ

На основі статистичних даних показника Y і фактора X, які надані у таблиці 2, та в припущенні, що стохастична залежність між фактором X і показником Y має вигляд: y=bx^a, застосувати заміну змінних, що зводить стохастичну залежність до лінійної між X₁ і Y₁: Y₁=a₁x₁+b₁.

Використовуючи пакет електронних таблиць Excel, зробити наступну роботу.

1. Знайти оцінки:

   • коефіцієнта кореляції R;

   • параметрів a₁, b₁ допоміжної лінії регресії Y=a₁X+b₁ та параметрів a, b шуканої лінії регресії y=bx^a.

2. Використовуючи критерій Фішера, з надійністю P=0,95 перевірити статистичну гіпотезу про адекватність прийнятої економічної моделі статистичним даним.

3. Якщо модель адекватна статистичним даним, то знайти прогноз показника Y_1p та його надійний інтервал.

4. Якщо модель адекватна статистичним даним, то знайти коефіцієнт еластичності К_el для базисних даних і прогнозу.

5. Побудувати графіки статистичних даних, лінії регресії і коефіцієнта еластичності.

6. На основі одержаної економетричної моделі зробити висновки.

Таблиця 2 – Статистичні дані

Y	10	10	18	30	47	55	45	72	108	93	140	134	213	196	251
X	3	3,50	4	4,5	5	5,5	6	6,5	7	7,5	8	8,5	9	9,5	10

ХІД РОБОТИ

Вводиться гіпотеза, що між фактором X та показником Y існує стохастична залежність y=bx^a

Перетворимо нелінійну регресію y=bx^a до лінійної. Візьмемо логарифми від обох частин рівності. Одержимо ln(y)=ln(bx^a), ln(y)=ln(b)+aln(x).

Заміною y₁=ln(y), x₁=ln(x), b₁=ln(b), a₁=a, одержимо рівняння допоміжної лінії регресії y₁=a₁x₁+b₁. Із рівностей b₁=ln(b) та a₁=a маємо, що a=a₁ та b=exp(b₁).

Для роботи використовується пакет Excel. Значення фактору Х запишемо в діапазоні В3:B18, а значення показника Y в діапазоні А3:А17. Прогнозні значення обчислюються в 18-ому рядку.

В діапазони C3:C17 та D3:D18 запишемо значення Y₁=Ln(Y) та X₁=Ln(X) відповідно, де Ln – вбудована математична функція. У діапазоні E3:E17 знаходимо добуток Y₁·X₁, в інтервалі F3:F17 – значення X₁². Для визначення сум стовпців у 19 рядку використовуємо кнопку автосумування або функцію СУММ( ).

Оцінки параметрів a₁ і b₁ парної регресії обчислюються за формулами 2.1 та 2.2:

(2.1)

(2.2)

Отримані значення запишемо в комірки С21 та С22 відповідно. Значення коефіцієнтів a та b рівняння нелінійної регресії визначаються в комірках С23 та С24 відповідно. Середні значення X_1с, Y_1с та Y_с обчислюються в комірках E20, E21, E22 з використанням вбудованої статистичної функції СРЗНАЧ ( ).

Для обчислення теоретичних значень Y_1р у стовпчику G3:G17 вводимо формулу a₁X_1i+b₁ з абсолютним посиланням координат-параметрів a₁ і b₁ та відносним посиланням координати X_1i. У комірці G19 визначається сума діапазону G3:G17. Оскільки математичне сподівання відхилення фактичних даних від розрахункових дорівнює нулю, то при правильному виконанні розрахунків значення комірок C19 та G19 співпадатимуть.

Значення (Y₁-Y_1P)² обчислюємо в діапазоні H3:H17, а їх суму визначаємо в комірці H19. Для оцінки адекватності прийнятої економетричної моделі експериментальним даним використаємо критерій Фішера. Для визначення розрахункового значення критерію Фішера, оцінки довірчої зони базисних даних та оцінки довірчого інтервалу прогнозу створюємо блок проміжних обчислень J3:L17.

Теоретичні значення Y_р обчислюємо у діапазоні I3:I17 за формулою bx^a з абсолютним посиланням координат-параметрів a і b та відносним посиланням координати X_i. У комірці I19 визначається сума діапазону I3:I17. Можна також підраховувати значення Y_р в комірці I3, як експоненту від значення Y_1р.

Значення (Y_i-Y_Pi)², (Y_i-Y_c)², (X_1i-Y_1c)² обчислюємо відповідно в діапазонах J3:J17, K3:K17, L3:L17, а їх суми в комірках J19, К19, L19. Значення критерію значимості рівняння регресії S обраховуємо за формулою 2.3 у комірці E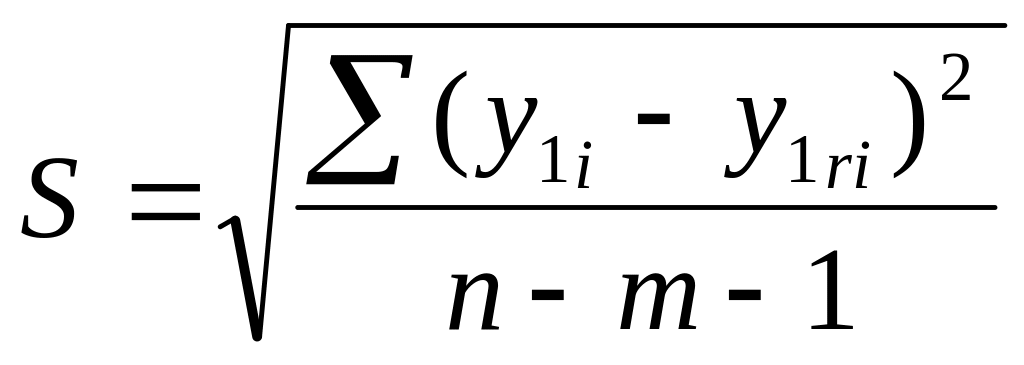23:

(2.3)

Визначимо коефіцієнт кореляції та розрахунковий коефіцієнт Фішера за формулами 1.4 та 1.5 із попередньої роботи. Результати запишемо у комірки G20 та G21 відповідно.

Табличне значення F-критерію для ймовірності α=0,05 і числа ступенів вільності k₁=m, k₂=n-m-1 визначаємо в комірці G22 за допомогою статистичної функції FРАСПОБР із параметрами 0,05; 1; 13.

В комірці I21 визначаємо коефіцієнт Ст’юдента за допомогою статистичної функції СТЬЮДРАСПОБР( ) із імовірністю 0,05 та ступеню вільності k=n-m-1.

Для знаходження інтервального прогнозу потрібно визначити в діапазоні M3:M17 величину приросту за формулою 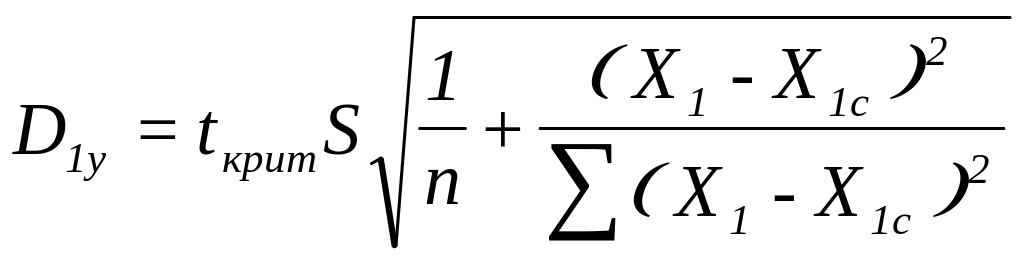2.4.

(2.4)

Значення Y_1min, Y_1max обчислюються відповідно в діапазонах N3:N18, O3:O18 за формулами Y_1р–D_1y Y_1р+D_1y. Межі Y_min та Y_max для інтервального прогнозу обчислюються відповідно в діапазонах P3:P18, Q3:Q18 за допомогою формули EXP( ).

Коефіцієнт еластичності для базисних значень та прогнозу обчислюється в діапазоні R3:R18 за формулою 2.5.

(2.5)

Для наочного відображення одержаних розрахунків будуємо графіки: фактичних даних Y, лінії регресії для базисних даних та прогнозу Y_p, довірчу зону для базисних даних і прогнозу Y_min, Y_max, коефіцієнта еластичності K_el.

Результати виконаних розрахунків можна побачити на рисунку 2.

Рисунок 2 – Оцінка параметрів нелінійної регресії

ВИСНОВКИ

1. Оскільки F_роз >F_крит, то з надійністю Р=0,95 можна вважати, що прийнята математична модель адекватна експериментальним даним, і на основі цієї моделі можна здійснювати економічний аналіз та знаходити значення прогнозу.

2. Для Х_р=11 точкова оцінка прогнозу показника має значення Y_p=317,33. З ймовірністю Р=0,95 прогноз показника буде набувати значення в інтервалі (202,97; 496,15).

3. Для прогнозу зміна фактора на 1% викличе зміну показника в середньому на 2,76%.