Міністерство освіти і науки, молоді та спорту України

Полтавський національний технічний університет

імені Юрія Кондратюка

Кафедра економічної кібернетики

Методичні вказівки

до виконання лабораторних робіт

із дисципліни «ЕКОНОМІКО-МАТЕМАТИЧНІ МЕТОДИ ТА МОДЕЛІ: ЕКОНОМЕТРИКА»

МОДУЛЬ 1

для студентів напрямів підготовки:

6.030502 «Економічна кібернетика»,

6.030507 «Маркетинг», 6.030509 «Облік і аудит»

всіх форм навчання

Полтава 2012

Методичні вказівки до виконання лабораторних робіт із дисципліни «Економіко-математичні методи та моделі: економетрика» (Модуль 1) для студентів напрямів підготовки 6.030502 «Економічна кібернетика», 6.030507 «Маркетинг», 6.030509 «Облік і аудит» всіх форм навчання. – Полтава: ПолтНТУ, 2012. – 29 с.

Укладачі: старший викладач О.Г. Климко, асистент С.А. Щербініна.

Відповідальний за випуск: Р.Г.Савенко, завідувач кафедри економічної кібернетики, доктор техн. наук, професор.

Рецензент: М.В.Лисенко, канд. фіз.-мат. наук, доцент.

Затверджено науково-методичною радою університету

від ________20__ р., протокол № __

Авторська редакція О.Г. Климко,

С.А.Щербініна

59.40.15.02

ВСТУП

Основне призначення економіки – забезпечення суспільства предметами споживання та послугами, котрі створюють умови для життя та безпеки людини, родини, суспільства, країни. У зв’язку з цим є сенс розглядати та досліджувати соціально-економічні системи.

Основним інструментальним та ефективним методом дослідження систем є метод моделювання, тобто спосіб теоретичних і практичних дій, спрямованих на створення та використання моделей. Математична модель – це абстракція реальної дійсності (світу), в якій відношення між реальними елементами замінені відношеннями між математичними категоріями. Ці відношення зазвичай подаються у формі рівнянь і/чи нерівностей, відношеннями формальної логіки між показниками (змінними), які характеризують функціонування реальної системи, що моделюється.

Практичними завданнями економіко-математичного моделювання є: по-перше – аналіз економічних суб’єктів і процесів; по-друге – економічне прогнозування, передбачення розвитку економічних процесів; по-третє – вироблення управлінських рішень на всіх рівнях господарської ієрархії управління.

Економетрія – наука, яка вивчає методи оцінювання параметрів моделей, які характеризують кількісні взаємозв’язки між економічними показниками, а також розглядає основні напрямки застосування цих моделей в економічних дослідженнях.

Залежно від способу вираження співвідношень між зовнішніми умовами, внутрішніми параметрами та характеристиками, які мають бути знайдені, математичні моделі поділяються на дві групи: структурні та функціональні.

Економетричні моделі належать до функціональних моделей. Вони кількісно описують зв’язок між вхідними показниками економічної системи (Х) та результативним показником (Y). У загальному вигляді економетричну модель можна записати так:

де Х – вхідні економічні показники; u – випадкова, або стохастична, складова.

Побудова і дослідження економетричних моделей мають ряд особливостей. Ці особливості пов’язані з тим, що економетричні моделі є стохастичними. Вони кількісно описують кореляційно-регресійний зв’язок між економічними величинами. Отже, щоб побудувати економетричну модель, необхідно:

1. мати достатньо велику сукупність спостережень даних;

2. забезпечити однорідність сукупності спостережень;

3. забезпечити точність вхідних даних.

Студенти мають знати теоретичний матеріал, що включає опис та алгоритмізацію методів оцінки параметрів моделі, вміти застосовувати ці методи для кількісного виміру взаємозв’язку між конкретними економічними показниками, враховуючи особливості вихідної інформації, робити відповідні висновки.

Лабораторна робота №1 Парна лінійна регресія

ЗАВДАННЯ

На основі статистичних даних показника Y і фактора X, які надані у таблиці 1, для лінійної економетричної моделі Y=aX+b, використовуючи пакет електронних таблиць Excel, зробити наступну роботу:

1) Знайти оцінки:

• коефіцієнта кореляції R;

• параметрів a,b лінії регресії Y=aX+b.

2) Використовуючи критерій Фішера, з надійністю P=0,95 перевірити статистичну гіпотезу про адекватність прийнятої економічної моделі статистичним даним.

3) Якщо модель адекватна статистичним даним, то знайти прогноз показника Y_p та його надійний інтервал.

4) Якщо модель адекватна статистичним даним, то знайти коефіцієнт еластичності К_ел для базисних даних і прогнозу.

5) Побудувати графіки статистичних даних Y, лінії регресії для базисних даних та прогнозу, довірчої зони для базисних даних і прогнозу Y_min, Y_max та коефіцієнт еластичності K_ел.

6) На основі одержаної економетричної моделі зробити висновки.

Таблиця 1 – Статистичні дані

Y	30	30	33	35	34	35	38	40	42	44	46	47	49
X	1	1,5	2	2,5	3	3,5	4	4,5	5	5,5	6	6,5	7

ХІД РОБОТИ

Вводиться гіпотеза, що між фактором X та показником Y існує лінійна стохастична залежність Y=aX+b.

Оцінки параметрів a і b парної регресії обчислюються за формулами 1.1. та 1.2.:

(1.1)

(1.2)

Для роботи використовується пакет Excel. Блок вихідних даних формується в перших двох стовпцях A3:B15. За блоком вихідних даних іде блок проміжних розрахунків C3:L15. Прогнозні значення обчислюються в 16-ому рядку.

У стовпчику C знаходимо добуток Y*X та у стовпчику D – значення X². Для визначення сум стовпців використовуємо кнопку автосумування або вбудовану функцію СУММ(ЧИСЛО). В клітинки B19, B20 вводимо формули для визначення оцінок параметрів відповідно a і b. Середні значення Xc, Yc обчислюються в клітинках D18, D19 з використанням вбудованої статистичної функції СРЗНАЧ(ЧИСЛО).

Для обчислення Y_p у стовпчик E вводимо формулу ax_i+b з абсолютним посиланням координат-параметрів a і відносним посиланням координати x_і. У клітинці E17 буде знаходитись сума блоку E3:E15. Оскільки математичне сподівання відхилення фактичних даних від розрахункових дорівнює нулю, то при правильному виконанні розрахунків значення клітинок A17 та E17 співпадатимуть.

Для оцінки адекватності прийнятої економетричної моделі експериментальним даним використаємо критерій Фішера. Для визначення розрахункового значення критерію Фішера, оцінки довірчої зони базисних даних та оцінки довірчого інтервалу прогнозу створюємо блок проміжних обчислень F3:K15.

Значення (Y-Y_p)², (Y-Y_c)², (X-X_c)² обчислюємо відповідно в блоках F3:F15, G3:G15, H3:H15, а їх суми в блоці F17:H17.

Значення критерію значимості рівняння регресії S обчислюється у клітинці D20 за формулою 1.3.

, (1.3)

де n – кількість спостережень,

m – кількість коефіцієнтів при змінних в рівнянні регресії.

Значення коефіцієнта кореляції R розраховується в клітинці F18:

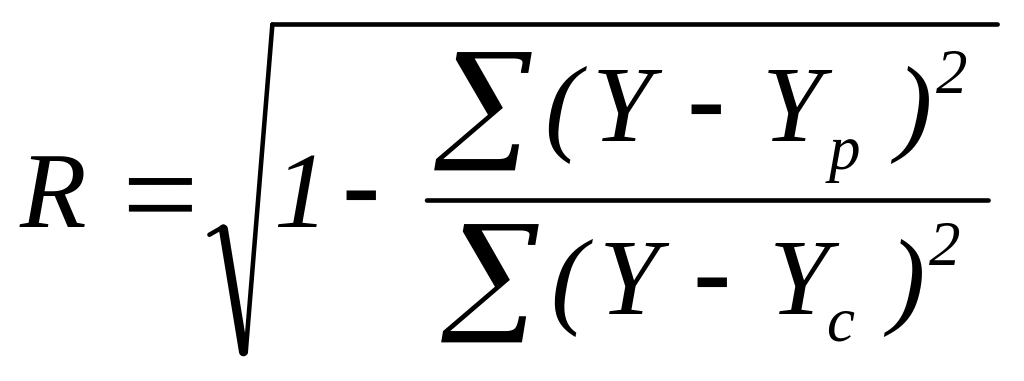(1.4)

Коефіцієнт кореляції характеризує ступінь щільності лінійної залежності між випадковими величинами X,Y і змінюється в межах від -1 до 1. Якщо K_кор>0, то між випадковими величинами X і Y існує пряма залежність, якщо K_кор<0, то між цими випадковими величинами існує обернена залежність.

Розрахункове значення критерію Фішера F_роз – в клітинці F19:

(1.5)

Табличне критичне значення критерію Ст’юдента t_крит розраховується в клітинці H19 за допомогою статистичної функції СТЬЮДРАСПОБР(), з імовірністю 0,05 та степеню вільності k₁=n-m-1.

Значення приросту D_y – в блоці I3:I15 за формулою 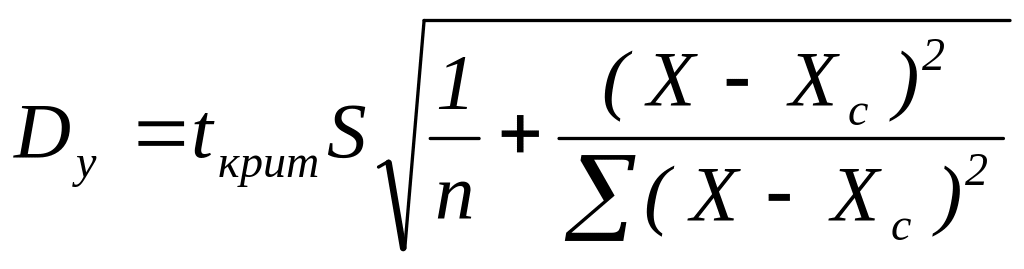(1.6):

(1.6)

Для приросту D_y прогнозного значення використовується наступна формула:

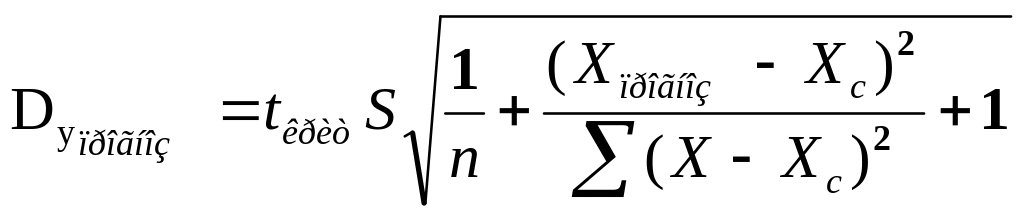
(1.7)

Значення Y_min=Y_p–D_y, Y_max=Y_p+D_y обчислюються відповідно в блоках J3:J15, K3:K15.

Критичне (табличне) значення критерію Фішера розраховується в клітинці F20 за допомогою статистичної функції FРАСПОБР( ) з імовірністю 0,05 та степенями вільності k₁=m та k₂=n-m-1.

Коефіцієнт еластичності К_ел відображає, на скільки відсотків зміниться показник Y при зміні фактору X на один відсоток. Він обраховується для базисних значень та прогнозу в блоці L3:L15 за формулою 1.8:

(1.8)

Результати виконаних розрахунків можна побачити на рисунку 1.

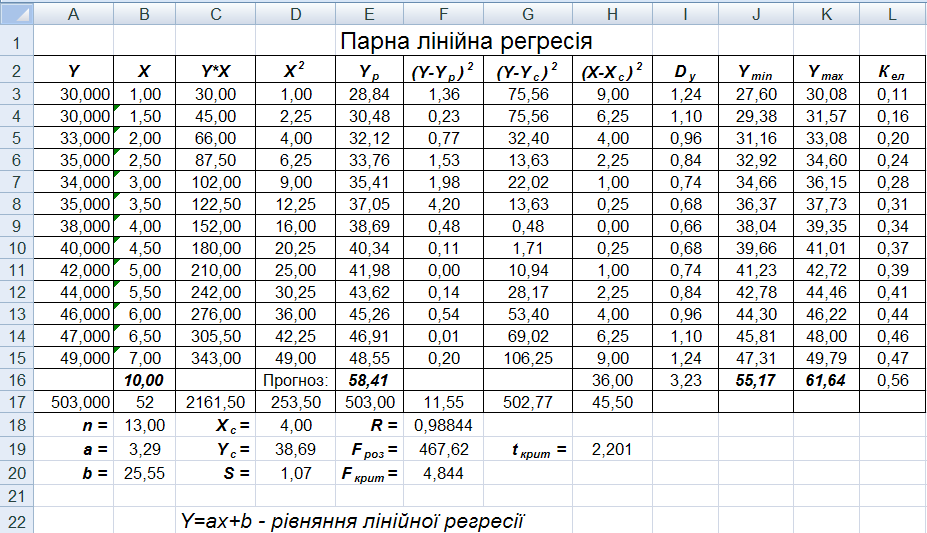
Рисунок 1 – Оцінка параметрів лінійної парної регресії

ВИСНОВКИ

1. Для лінійної економетричної моделі Y=aX+b знайдено оцінки коефіцієнта кореляції К_кор=0,99 та параметрів a=3,29, b=25,55. Отже, рівняння лінійної регресії – Y=3,29X+25,55.

2. Оскільки F_роз= 467,62> F_крит =4,844, то з надійною ймовірністю Р=0,95 можна вважати, що прийнята математична модель адекватна експериментальним даним, і на основі цієї моделі можна здійснювати економічний аналіз та знаходити значення прогнозу.

3. Для фактора X_р=10 точкова оцінка прогнозу показника має значення Y_р=58,41. З надійною ймовірністю Р=0,95 прогноз показника буде набувати значення в інтервалі (55,17; 61,64).

4. Для прогнозу зміна фактора на 1% викличе зміну показника в середньому на 0,56%.