Задачи для самостоятельного решения

Два абсолютно жестких стержня АВ и АС соединены шарниром в точке А и прикреплены к неподвижной поверхности шарнирами В и С, образуя с ней углы, указанные на рис. 2.13. К валику шарнира А подвешен на нерастяжимой нити груз D, вес которого Р и груз D₁, вес которого Р₁. Углы между стержнями и веса грузов указаны в таблице 1. Определить усилия, возникающие в стержне АВ и АС. Весом стержней и нити пренебречь.

Таблица 2.1

Вариант	1	2	3	4	5	6	7	8	9	10
	для рис. 1 ‑ 4				для рис. 5, 6		для рис. 7‑10
α (град)	30	45	40	50	50	35	30	25	45	40
β (град)	45	35	50	35	-	-	50	70	55	60
Р (Н)	100	200	300	400	100	300	100	200	300	400
Р1 (Н)	-	-	-	-	-	-	350	250	150	100
Вариант	11	12	13	14	15	16	17	18	19	20
	для рис. 1‑4				для рис. 5, 6		для рис. 7‑10
α (град)	35	55	45	60	45	55	35	20	40	55
β (град)	60	35	50	45	-	-	70	80	65	25
Р (Н)	200	300	400	100	200	400	400	300	200	100
Р1 (Н)	-	-	-	-	-	-	150	250	350	400
Вариант	21	22	23	24	25	26	27	28	29	30
	для рис. 1‑4				для рис. 5, 6		для рис. 7‑10
α (град)	20	55	45	60	40	65	45	30	45	55
β (град)	60	25	20	35	-	-	70	80	65	55
Р (Н)	300	200	100	400	300	200	200	400	100	300
Р1 (Н)	-	-	-	-	-	-	250	150	400	350

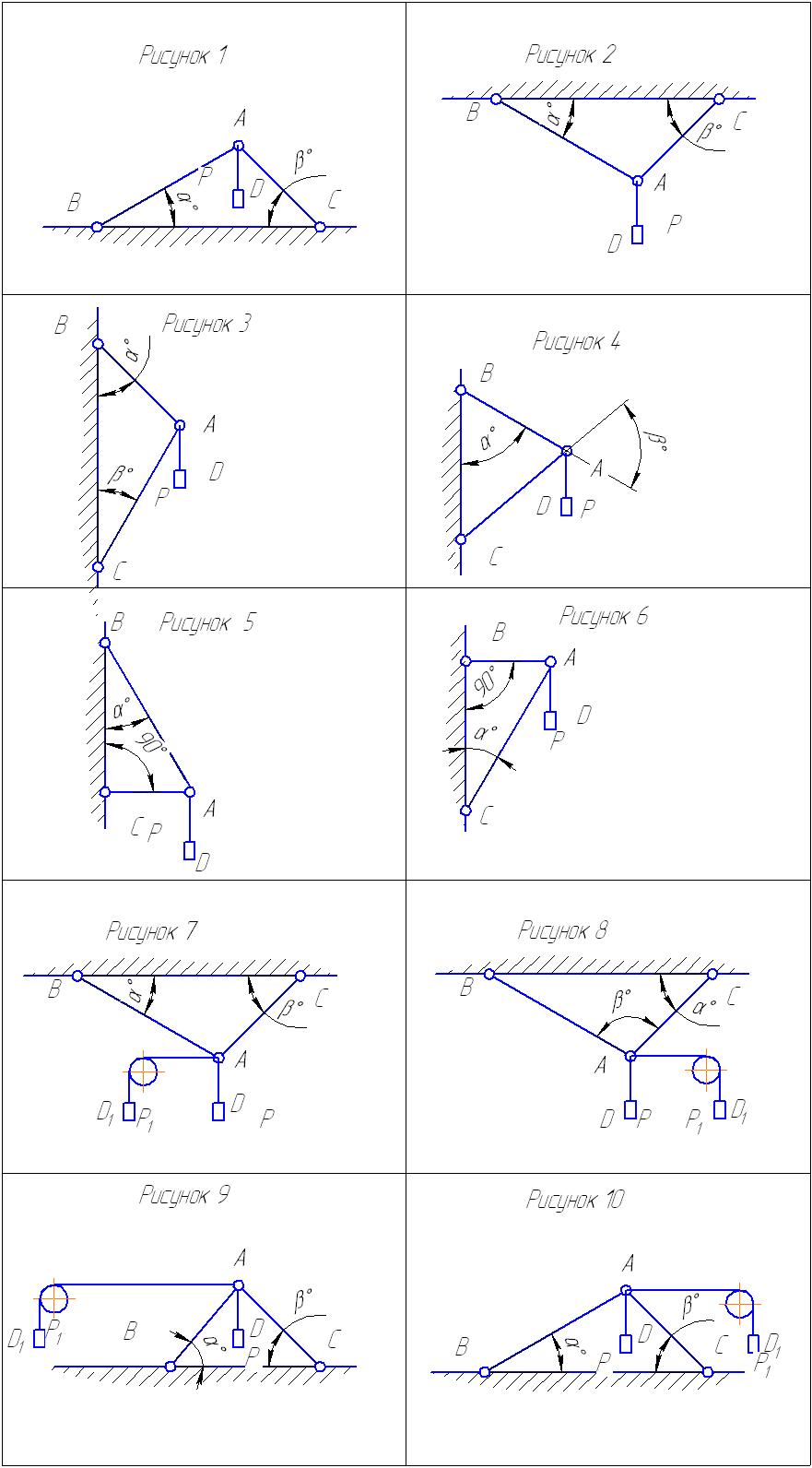
Рис. 2.13

3. Пара сил и моменты сил

3.1. Пара сил и ее действие на тело. Эквивалентность пар

Две равные и параллельные силы, направленные в противоположные стороны и не лежащие на одной прямой, называются парой сил (рис.3.1).

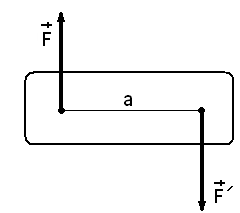
Рис. 3.1

Сумма проекций сил пары на ось x и ось y равна нулю, поэтому пара сил не имеет равнодействующей. Несмотря на это, тело под действием пары сил не находится в равновесии.

Действие пары сил на твердое тело состоит в том, что она стремится вращать это тело. Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние (взятое по перпендикуляру к силам) между линиями действия сил. Обозначим момент пары М, а кратчайшее расстояние между силами а, тогда абсолютное значение момента пары сил:

М = F·a = F '·а.

Кратчайшее расстояние между линиями действия сил а называется плечом пары.

Эффект действия пары сил полностью определяется ее моментом. Поэтому момент пары сил можно показывать дугообразной стрелкой, указывающей направление вращения. Так как пара сил не имеет равнодействующей, ее нельзя уравновесить одной силой. Момент пары в СИ измеряется в ньютон-метрах (Н·м) или в единицах, кратных ньютон-метру: кН·м, МН·м и т. д.

Момент пары сил будем считать положительным, если пара стремится повернуть тело по направлению хода часовой стрелки, и отрицательным, если пара стремится вращать тело против хода часовой стрелки (рис. 3.2). Принятое правило знаков для моментов пар условно: можно было бы принять про­тивоположное правило.

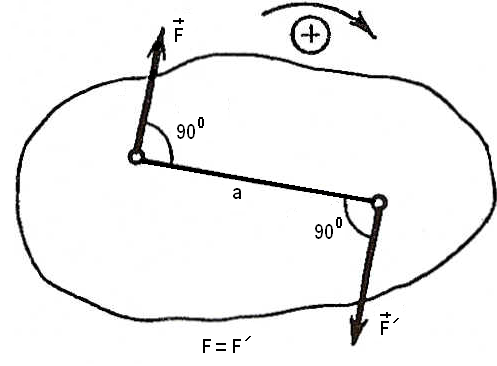
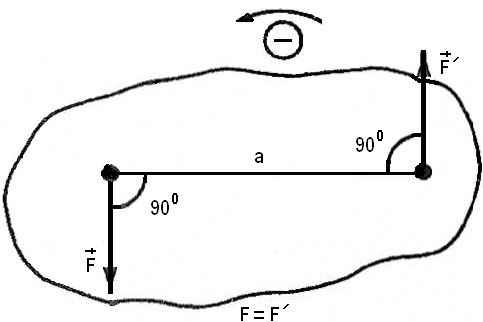
Рис. 3.2

Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой парой механическое состояние тела не изменяется, т. е. не изменяется движение тела или не нарушается его равновесие.

Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Следовательно, пару сил можно переносить в плоскости ее действия в любое положение.

Не нарушая состояния тела, можно как угодно изменять модули сил и плечо пары, лишь бы момент пары оставался неизменным.

Подобно силам, пары можно складывать. Пара, заменяющая собой действие данных пар, называется результирующей.

Поскольку действие пары сил полностью определяется ее моментом и направлением вращения, то сложение пар производится алгебраическим суммированием их моментов, т. е. момент результирующей пары равен алгебраической сумме моментов составляющих пар.

Это применимо к любому количеству пар, лежащих в одной плоскости. Поэтому при произвольном числе слагаемых пар, лежащих в одной плоскости или параллельных плоскостях, момент результирующей пары определится по формуле

М = М₁ + М₂ + … + М_n = ,

где моменты пар, вращающиеся по часовой стрелке, принимаются положительными, а против часовой стрелки ‑ отрицательными.

Условие равновесия системы пар, лежащих в одной плоскости: для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары равнялся нулю или чтобы алгебраическая сумма моментов пар равнялась нулю:

М = = 0