2.2. Проекция силы на ось. Проекция векторной суммы сил на ось

Решение задач на равновесие сходящихся сил с помощью построения замкнутых силовых многоугольников сопряжено с громоздкими построениями. Универсальным методом решения таких задач является переход к определению проекций заданных сил на координатные оси и оперирование с этими проекциями. Осью называют прямую линию, которой приписано определенное направление.

Проекция вектора на ось является скалярной величиной, которая опреде­ляется отрезком оси, отсекаемым перпендикулярами, опущенными на нее из начала и конца вектора.

Проекция вектора считается положительной, если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной, если направление от начала проекции к ее концу противоположно положительному направлению оси.

Таким образом, проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.

Рассмотрим ряд случаев проецирования сил на ось.

Вектор силы F (рис. 2.2) составляет с положительным напра­влением оси х острый угол .

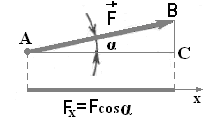
Рис. 2.2

Чтобы найти проекцию, из начала и конца вектора силы опускаем перпендикуляры на ось oх; получаем

1. F_x = F cos α

Проекция вектора в данном случае положительна

Сила F (рис. 2.3) составляет с положительным направлением оси х тупой угол α.

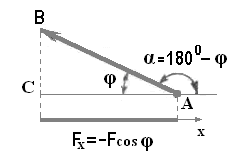
Рис. 2.3

Тогда F_x = F cos α, но так как α = 180⁰ - φ,

F_x = Fcos α = Fcos180⁰ - φ =- Fcos φ.

Проекция силы F на ось oх в данном случае отрицательна.

Сила F (рис. 2.4) перпендикулярна оси oх.

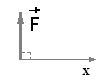
Рис. 2.4

Проекция силы F на ось х равна нулю

F_x = F cos 90° = 0.

Силу, расположенную на плоскости хоу (рис. 2.5), можно спроектировать на две координатные оси ох и оу.

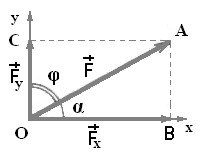
Рис. 2.5

Силу F можно разложить на составляющие: F_x и F_y. Модуль вектора F_x равен проекции вектора F на ось ox, а модуль вектора F_y равен проекции вектора F на ось oy.

Из ΔОАВ: F_x=F cos α, F_x=F sin α.

Из ΔОАС: F_x=F cos φ, F_x=F sin φ.

Модуль силы можно найти по теореме Пифагора:

.

Проекция векторной суммы или равнодействующей на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.

Рассмотрим сходящиеся силы F₁, F₂, F₃, и F₄, (рис. 2.6, а). Геометрическая сумма, или равнодействующая, этих сил F определяется замыкающей стороной силового многоугольника

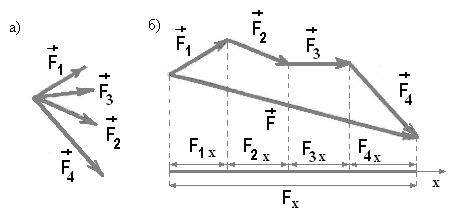
Рис. 2.6

Опустим из вершин силового многоугольника на ось x перпендикуляры.

Рассматривая полученные проекции сил непосредственно из выполненного построения, имеем:

F= F_1x+F_2x+F_3x+ F_4x

или

,

где n ‑ число слагаемых векторов. Их проекции входят вышеуказанное уравнение с соответствующим знаком.

В плоскости геометрическую сумму сил можно спроецировать на две координатные оси, а в пространстве – соответственно на три.

2.3. Условие равновесия плоской системы сходящихся сил

При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого (рис. 2.7).

Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.

Если в системе три силы, образуется треугольник сил.

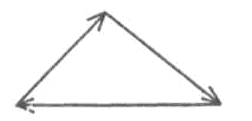
Рис. 2.7

При аналитическом способе определения равнодействующей условие равновесия, означающее равенство нулю равнодействующей, принимает следующую форму:

.

F_Σ = 0.

Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Следовательно, условие равновесия выглядит следующим образом:

 F_x=0;

 F_y=0.

В задачах координатные оси выбирают так, чтобы решение было наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.