9.1.2. Внутренние силы. Метод сечений

Все материалы, элементы конструкций и конструкции под действием внешних сил в той или иной мере испытывают смещения (перемещения относительно нагруженного состояния) и изменяют свою форму (деформируются). Взаимодействие между частями (частицами) внутри элемента конструкции характеризуется внутренними силами.

Внутренние силы − силы межатомного взаимодействия, возникающие при воздействии на тело внешних нагрузок и стремящиеся противодействовать деформации.

Для расчета элементов конструкций на прочность, жесткость и устойчивость необходимо с помощью метода сечений определить возникающие внутренние силовые факторы.

Суть метода сечений заключается в том, что внешние силы, приложенные к отсеченной части тела, уравновешиваются внутренними силами, возникающими в плоскости сечения и заменяющими действие отброшенной части тела на остальную.

Стержень, находящийся в равновесии под действием сил F₁, F₂, F₃, F₄, F₅ (рис.9.4, а), мысленно рассечем на две части I и II (рис. 9.4, б) и рассмотрим одну из частей, например левую.

Так как связи между частями устранены, то действие одной из них на другую следует заменить системой внутренних сил в сечении. Поскольку действие равно противодействию и противоположно по направлению, то внутренние силы, возникающие в сечении, уравновешивают внешние силы, приложенные к оставленной части.

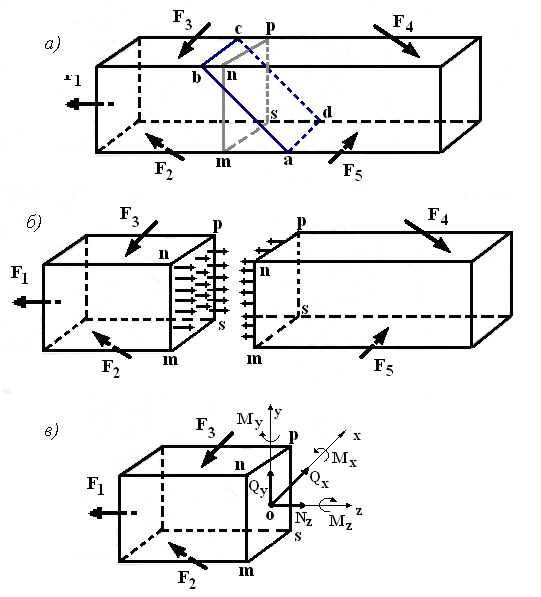
Рис. 9.4

Поместим в точку О систему координат xyz. Разложим главный вектор и главный момент на составляющие, направленные по координатным осям:

;

Составляющая N _z - называемая продольной (нормальной) силой, вызывает деформацию растяжения или сжатия. Составляющие Q _x и Q _y перпендикулярны нормали и стремятся сдвинуть одну часть тела относительно другой, их называют поперечными силами. Моменты M_x и M_y изгибают тело и называются изгибающими. Момент M_z скручивающий тело называют крутящим. Эти силы и моменты, являются внутренними силовыми факторами (рис.9.4, в).

Отыскать составляющие главного вектора и главного момента внутренних сил позволяют условия равновесия:

;

;

В частных случаях отдельные внутренние силовые факторы могут быть равны нулю. Так, при действии плоской системы сил (например, в плоскости zy) в его сечениях возникают силовые факторы: изгибающий момент M_x, поперечная сила Q_y, продольная сила N_z. Условия равновесия для данного случая:

;

.

Для определения внутренних силовых факторов необходимо:

1. Мысленно провести сечение в интересующей нас точке конструкции или стержня.

2. Отбросить одну из отсеченных частей и рассмотреть равновесие оставленной части.

3. Составить уравнения равновесия для оставленной части и определить из них значения и направления внутренних силовых факторов.

Внутренние силовые факторы, возникающие в поперечном сечении стержня, определяют деформированное состояние.

Метод сечений не позволяет установить закон распределения внутренних сил по сечению.

Эффективными характеристиками для оценки нагруженности деталей будет интенсивность внутренних сил взаимодействия — напряжение и деформация.

Рассмотрим сечение тела (рис.9,5). На основании принятого ранее допущения о том, что рассматриваемые тела сплошные, можно считать, что внутренние силы непрерывно распределены по всему сечению.

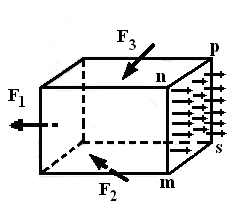
Рис. 9.5

В сечении выделим элементарную площадку ΔА, а равнодействующую внутренних сил на этой площадке обозначим ΔR. Отношение равнодействующей внутренних сил ΔR на площадке ΔА к величине площади этой площадки называется средним напряжением на данной площадке:

Если площадку ΔА уменьшать (стягивать в точку), то в пределе получим напряжение в точке

Силу ΔR можно разложить на составляющие: нормальную ΔN и касательную ΔQ. По этим составляющим определяют нормальное σ и касательное τ напряжения (рис.9.6):

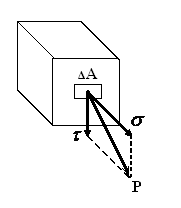
Рис. 9.6

Для измерения напряжений в Международной системе единиц (СИ) служит ньютон на квадратный метр, названный паскалем Па (Па = Н/м²). Так как эта единица очень мала и пользоваться ею неудобно, применяют кратные единицы (кН/м², МН/м² и Н/мм²). Отметим, что 1 МН/м² = 1МПа = 1Н/мм². Эта единица наиболее удобна для практического использования.

В технической системе единиц (МКГСС) для измерения напряжений применяли килограмм-силу на квадратный сантиметр. Соотношение между единицами измерения напряжений в Между­народной и технической системах устанавливается на основе соотношения между единицами сил: 1 кгс = 9,81 Н 10 Н. Приближенно можно считать: 1 кгс/см² = 10 Н/см² = 0,1 Н/мм² = 0,1 МПа или 1 МПа = 10 кгс/см².

Нормальные и касательные напряжения являются удобной мерой оценки внутренних сил тела, так как материалы различным образом им сопротивляются. Нормальные напряжения стремятся сблизить или удалить отдельные частицы тела по направлению нормали к плоскости сечения, а касательные напряжения стремятся сдвинуть одни частицы тела относительно других по плоскости сечения. Поэтому касательные напряжения называют еще напряжениями сдвига.

Деформация нагруженного тела сопровождается изменением расстояний между его частицами. Внутренние силы, возникающие между частицами, изменяются под действием внешней нагрузки до тех пор, пока не установится равновесие между внешней нагрузкой и внутренними силами сопротивления. Полученное состояние тела называют напряженным состоянием. Оно характеризуется совокупностью нормальных и касательных напряжений, действующих по всем площадкам, которые можно провести через рассматриваемую точку. Исследовать напряженное состояние в точке тела — значит получить зависимости, позволяющие определить напряжения по любой площадке, проходящей через указанную точку.

Напряжение, при котором происходит разрушение материала или возникают заметные пластические деформации, называют предельным и обозначают σ _пред ; τ _пред.. Эти напряжения определяют опытным путем.

Чтобы избежать разрушения элементов сооружений или машин, возникающие в них рабочие (расчетные) напряжения (σ, τ) не должны превышать допускаемых напряжений, которые обозначают в квадратных скобках: [σ], [τ]. Допускаемые напряжения — это максимальные значения напряжений, обеспечивающие безопасную работу материала. Допускаемые напряжения назначаются как некоторая часть экспериментально найденных предельных напряжений, определяющих исчерпание прочности материала:

где [n] — требуемый или допускаемый коэффициент запаса прочности, показывающий, во сколько раз допускаемое напряжение должно быть меньше предельного.

Коэффициент запаса прочности зависит от свойств материала, характера действующих нагрузок, точности применяемого метода расчета и условий работы элемента конструкции.

Под действием сил возникают смещения не только в конструкции, но и в материале, из которого она изготовлена (хотя во многих случаях такие перемещения находятся далеко за пределами возможностей невооруженного глаза и обнаруживаются с помощью высокочувствительных датчиков и приборов).

Для определения деформаций в точке К рассмотрим малый отрезок KL длиной s, исходящий из этой точки в произвольном направлении (рис.9.7).

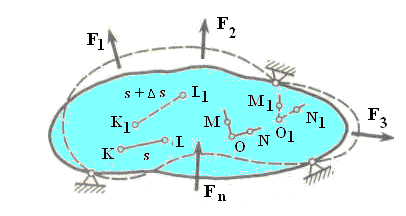
Рис. 9.7

В результате деформации точки К и L переместятся в положение К₁ и L₁ соответственно, а длина отрезка возрастет на величину Δs. Отношение

представляет собой среднее удлинение на отрезке s.

Уменьшая отрезок s, приближая точку L к точке К, в пределе получим линейную деформацию в точке К по направлению KL:

Если в точке К провести три оси параллельные осям координат, то линейные деформации в направлении координатных осей х, у и z будут равны соответственно ε_x , ε_y, ε_z.

Деформация тела является безразмерной и часто выражается в процентах. Обычно деформации невелики и в условиях упругости не превышают 1 − 1,5 %.

Рассмотрим прямой угол, образованный в недеформированном теле отрезками ОМ и ON (рис. 9.7). В результате деформации под действием внешних сил угол MON изменится и станет равным углу M₁O₁N₁. В пределе разность углов называют угловой деформацией или деформацией сдвига в точке О в плоскости MON:

В координатных плоскостях угловые деформации или углы сдвига обозначаются: γ_xy, γ_yx, γ_xz.

В любой точке тела имеют место три линейных и три угловых компонента деформации, которые определяют деформированное состояние в точке.