I1,i2,i3,i4 – кривые безразличия

более предпочтительны, чем наборы на близлежащих к началу координат кривых.

2. Касательная, проведённая к любой точке кривой безразличия, имеет отрицательный угол наклона.

3. Кривые безразличия не пересекаются, так как в этом случае наборы, лежащие на кривых по-разному удалённых от начала координат имели бы одинаковую полезность для потребителя.

Чтобы понять, чем определяется конфигурация кривой безразличия, построим такую кривую для благ X и Y, где точки А и В – равноценные комбинации этих благ.

Переходя от А к В, потребитель сокращает потребление товара Y на ∆y=-2 в обмен на увеличение товара Х на ∆x=1, но общий уровень удовлетворения потребителя остаётся неизменным. Предельной нормой замены благом Х блага Y (MRS_xy – marginal rate of substitution) называется

количество блага Y, которое должно быть сокращено при увеличении блага Х на одну единицу так, чтобы степень удовлетворения потребителя не изменилась. ∆y

MRS_xy = - ── , U = const

∆x

Знак «-» означает, что изменения количества двух благ происходят в противоположных направлениях.

Таким образом, если потребитель при выборе другого набора желает остаться на той же кривой безразличия, то прирост полезности от добавленного количества блага х должен быть равен потере полезности от изъятого количества блага у. Следовательно, предельная норма замены благом Х блага Y может рассматриваться как отношение предельной полезности блага Х к предельной полезности блага Y.

Рис.5. Определение предельной нормы замены при переходе от набора А к набору В

i – кривая безразличия; Δx – прирост товара х, Δу – сокращение товара у

Поскольку MUx уменьшается по мере замены блага Х благом Y, а MU_y соответственно увеличивается, отношение MU_x/MU_y, равное MRS_xy, уменьшается. Это проявляется на графике в убывании углового коэффициента наклона касательной по мере движения вниз вдоль кривой безразличия и объясняет её вогнутый характер. А это означает, что в окрестности любой своей точки она находится выше касательной, проведённой к этой точке.

Следует отметить, что уменьшающаяся предельная норма замены в порядковой теории имеет тот же смысл, что и убывающая предельная полезность в количественной теории. Только в одном случае полезность оценивается в ютилах, а в другом – в объёме другого товара, которым потребитель готов пожертвовать.

В большинстве случаев кривые безразличия имеют вогнутый характер, однако условие уменьшающейся предельной нормы замены не всегда соблюдается. Например, когда блага являются взаимодополняющими (зубная щетка и зубная паста, коньки и ботинки к ним, лыжи и крепления и т.п.), поскольку эти блага не могут заменяться MRS_xy=0, а кривые безразличия принимают L-образную форму (см. рис.6).

Для двух совершенно взаимозаменяемых товаров кривые безразличия представляют собой прямые линии, имеющие отрицательный наклон. Это случай, когда оба блага воспринимаются покупателем одинаково, например Coca-Cola Light и диетическая Coca-Cola. В этом случае MRS – величина постоянная. На рис.7 показана ситуация, в которой потребителю безразлично, чем утолять жажду, так как замена одного продукта другим абсолютно равноценна, а если так, то MPS=1.

Рис.6. Жесткая взаимодополняемость благ

X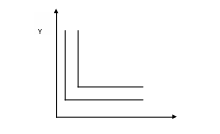

Как уже отмечалось ранее, выбор потребителя зависит не только от его предпочтений, но, увы, и от размера его кошелька. Иначе говоря, каковы бы ни были предпочтения покупателя, его возможности выбора ограничены его бюджетом.

В экономике существует понятие «бюджетного ограничения», что подразумевает, что общий расход должен быть не больше дохода. В настоящее время рост сбережений и развитие кредитных отношений в обществе позволяет обходить это ограничение (в США, например, большинство населения, живёт «в долг»), но мы в наших рассуждениях этот факт во внимание принимать не будем.

Рис.7. Совершенная взаимозаменяемость

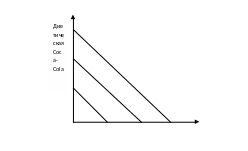
Сoca-Cola Light

Итак, если весь свой доход I потребитель тратит на покупку товаров Х и Y в количествах Q_x и Q_y и по ценам P_x и P_y, то бюджетное ограничение может быть записано как: I=P_x·Q_x+P_y ·Q_y. Решив это уравнение относительно Q_y, мы получим уравнение бюджетной линии:

P_x I

Q_y= - ─── · Q_x + ───

P_y P_y

Бюджетная линия B – это геометрическое место точек, представляющих наборы благ, покупка которых требует одинаковых затрат, при этом её наклон определяется соотношением цен товаров.

Пусть на покупку фруктов ежедневно выделяется 50 рублей. На эти деньги можно купить либо 10 яблок, либо 5 бананов. Отложим эти

Рис.8. Бюджетная линия

В1-В6 – бюджетная линия

количества на осях графика и соединим точки между собой (см. рис.8). У нас получилась бюджетная линия. Но если хочется и яблок и бананов, придется делать выбор. Комбинации количества яблок и бананов, доступные при данном бюджете представлены точками на бюджетной линии. Все наборы фруктов, соответствующие точкам на бюджетной линии, стоят ровно 50 рублей. Если набор будет представлен точкой, расположенной ниже бюджетной линии, то он обойдётся потребителю дешевле. А если набор представлен точкой выше бюджетной линии, это означает, что при данных финансовых возможностях он недоступен для покупателя.

Кривые безразличия и бюджетная линия используются для графической интерпретации ситуации потребительского равновесия. Равновесие потребителя соответствует такой комбинации покупаемых товаров, которая максимизирует полезность при имеющемся бюджетном ограничении.

Если совместить карту безразличия с бюджетной линией в одной системе координат, получится график равновесия потребителя (см. рис.9).

Рис.9. Равновесие потребителя

I – i2 – кривые безразличия; В0-В3 – комбинации товаров, доступные при данной бюджетной линии

Выбирая оптимальный набор, потребитель ставит перед собой две основные цели:

- потратить все имеющиеся деньги (доход), поэтому ему не интересны комбинации, находящиеся ниже бюджетной линии (В₀), а расположенные выше бюджетной линии наборы ему недоступны по средствам (В₄);

- занять максимально удалённую от начала координат кривую безразличия, чтобы получить максимальное удовлетворение от потраченного дохода.

Наборы В₁ и В₃ обеспечивают самый низкий уровень полезности. Двигаясь вдоль бюджетной линии от набора В₁ к набору В₂, потребитель переходит к более высокой кривой безразличия и, следовательно, увеличивает полезность.

Потребитель израсходует все деньги и получит максимально возможное удовлетворение, если он приобретёт комбинацию товаров, соответствующую точке, где бюджетная линия совпадает с касательной к наивысшей из доступных кривых безразличия (точка В₂). В этой точке наклон бюджетной линии равен наклону кривой безразличия, следовательно, условие равновесия может быть записано как

P_x d_y P_x

— = MPS_xy или — = —

P_y d_x P_y

То есть в точке потребительского оптимума предельная норма замены двух благ равна обратному отношению цен этих благ.

Показанное на рис.9 равновесие потребителя носит название внутреннего, так как точка оптимума В₂ лежит «внутри» графического двумерного пространства товаров. Но бывают случаи, когда бюджетная линия и кривая безразличия имеют разный наклон на всём их протяжении и их точка касания фактически отсутствует. Тогда оптимальное решение определяется положением, наиболее близким к касанию, и носит название «углового». Оно определяется пересечением бюджетной прямой с одной из осей координат и кривой безразличия (см. рис. 10).

На рисунке 10А) оптимум потребителя достигается в точке М, поскольку в предложенном варианте MPS_xy≤ P_x/P_y. Обратная ситуация изображена на рисунке 10Б), так как в этом случае MPS_xy≥ P_x/P_y и, значит оптимальное решение находится в точке N. Таким образом, «угловое» решение в порядковой теории полезности предполагает покупку только одного вида товаров. В реальной рыночной ситуации (многопродуктовая модель) «угловое» решение является скорее правилом, поскольку никто не покупает все виды товаров, которые продаются на рынке. Таким образом получается, что при заданных доходе и ценах потребитель выбирает на бюджетной линии точку, которая принадлежит самой удалённой от начала координат и, следовательно, самой полезной с учётом бюджетного ограничения кривой безразличия. Однако, рассматривая поведение потребителя в коротком и длительном временных периодах, следует обратить внимание на возможность изменения как цен, так и доходов, что неизбежно приведет к необходимости пересмотра сложившегося потребления.

Рис.10. «Угловое» решение потребительского выбора

А) Б)

Если цены остаются фиксированными, а доход возрастает, это даёт потребителю возможность приобретать те наборы товаров, которые раньше были для него недоступными, при этом бюджетная линия сдвигается дальше от начала координат. Если доход наоборот снижается, привычные наборы становятся недоступными, а бюджетная линия отодвигается ближе к началу координат. Такое смещение бюджетной линии приводит к новой точке равновесия потребителя, так как при каждом новом уровне дохода он будет выбирать самый полезный для себя набор благ. Если соединить все таким образом полученные точки равновесия на кривых безразличия, то получится кривая «доход-потребление», которая обозначается IEP (Income Expansion Path) или ICC (Income Consumption Curve). На рис.11 IEP представляет множество всех оптимальных наборов (Е, Е₁,Е₂) при изменении дохода потребителя (I‹ I₁‹ I₂) и неизменном соотношении цен ( P_x/P_y=const).

Линия IEP имеет положительный наклон, так как оба товара являются нормальными, то есть такими, что с ростом дохода растёт и их потребление. Однако, бывают такие ситуации, когда с ростом дохода потребление одного товара увеличивается, а другого сокращается. Линия IEP имеет отрицательный наклон, если один из товаров является низшим, то есть с ростом дохода потребителя его потребление сокращается (см. рис.12).

Рис.11. Линия «доход-потребление» IEP

i0 – i2 – кривые безразличия, B0 – B2 – бюджетные линии, E0 – E2 –точки равновесия потребителя IEP – линия «доход-потребление»

Рис.12. Линия «доход-потребление»

А) Б)

А) товар Х – низший; Б) товар Y – низший

На основании линии «доход-потребление» можно построить кривую Энгеля, напрямую выражающую зависимость между денежным доходом потребителя и количеством приобретаемого товара. Для нормальных товаров

кривая Энгеля имеет положительный наклон, но здесь возможны два варианта:

1. Угол наклона кривой возрастает с увеличением дохода потребителя, что свидетельствует о сокращении дополнительных количеств приобретаемого товара. Такой характер кривой типичен для продуктов питания (см.рис.13 А);

2. С ростом дохода уменьшается угол наклона кривой, так как возрастает приобретаемое количество товара. В основном это относится к приобретению товаров роскоши, получению образования, расходов на отдых и досуг (см. рис. 13 Б).

Следует отметить, что при достижении определённого уровня дохода, ряд товаров может переходить из нормальных в низшие. Например потребитель начинает предпочитать отдых в Турции отдыху на европейских курортах, вместо бижутерии приобретать ювелирные изделия из драгоценных металлов, наконец, просто заменить утреннюю овсянку мюсли (см. рис.13 В).

Рис.13 Кривые Энгеля

Теперь рассмотрим, какой будет реакция потребителя на изменение цен. Изменение цены на один из товаров при фиксированном доходе ведёт к изменению угла наклона бюджетной линии (смещение бюджетной линии), поскольку меняется соотношение цен товаров. Если цена на товар Х последовательно снижается (или наоборот, растёт), то каждому значению цены этого товара соответствует своя бюджетная линия. А каждая бюджетная линия соприкасается с какой-нибудь кривой безразличия. Таким образом, все точки касания будут представлять собой линию «цена-потребление», которая обозначается РЕР (Price Expansion Path). Если цена на товар Х последовательно снижается с P_x до P_x2 ,бюджетная линия сместится, и можно будет построить линию РЕР, что показано на рис.14. На отрезке от Е₀ до Е₁ при снижении цены с Р_х до Р_х1 увеличение потребления товара Х происходит за счёт уменьшения потребления товара Y. Угол наклона на этом

Рис.14. Линия «цена-потребление»

интервале отрицательный. Если цена продолжает снижаться, покупатель может позволить себе не только увеличение потребления товара Х, но и товара Y, о чём свидетельствует положительный наклон кривой РЕР на отрезке правее точки Е₁. Если цена товара Х продолжает снижаться, потребитель станет приобретать всё большие количества товара Y. На графике это показано направлением линии РЕР вверх, что говорит о том, что большая часть дохода покупателя тратится на приобретение товара Y.

На основании кривой РЕР можно построить линию индивидуального спроса на товар Х как функцию от его цены (см. рис.15).

Рассмотрим более подробно реакцию потребителя на снижение цены товара при неизменности цен прочих товаров и дохода потребителя. Возьмём к примеру набор фруктов, который включает некоторое количество бананов и яблок. Пусть цена на бананы снизилась. Это приведёт:

1. к росту покупательской способности потребителя: он сможет приобретать прежний набор фруктов, который ранее был для него оптимален, за меньшие деньги, а на сэкономленную сумму увеличить количество покупаемых бананов и яблок.

2. к увеличению потребления бананов и уменьшению потребления яблок, так как покупатель будет замещать относительно подорожавшие яблоки относительно подешевевшими бананами.

Эти два процесса и происходят одновременно и неотделимы друг от друга. Первый получил название эффекта дохода, а второй – эффекта замены. Под эффектом дохода понимается изменение спроса исключительно вследствие изменения реального дохода, а эффект замены означает изменение спроса на товар исключительно вследствие изменения его относительной цены.

Идея разложения общего эффекта изменения цены на эффект замены и эффект дохода принадлежит российскому экономисту и математику Е.Е.Слуцкому. В дальнейшем его идеи легли в основу работ англичанина Дж. Хикса.

Рис.15. Линия индивидуального спроса.

Версии Слуцкого и Хикса отличаются разными подходами к определению реального дохода. По Хиксу, разные уровни денежного дохода, обеспечивающие один и тот же уровень удовлетворения, представляют один и тот же уровень реального дохода. По Слуцкому – лишь тот уровень денежного дохода, который достаточен для приобретения одного и того же набора товаров, обеспечивает и неизменный уровень реального дохода.

Рассмотрим на графике модель разложения общего эффекта изменения цены на эффект замещения и эффект дохода по Хиксу (см. рис.16).

Пусть KL – исходная бюджетная линия. Ей соответствует исходная точка равновесия потребителя Q₀. Количество потребляемых бананов (товар Х) в точке Q₀ равно Х₀. Снижение цены на бананы приведёт к смещению бюджетной линии в положение KL₁, которой соответствует новая точка равновесия Q₁. Количество потребляемых бананов в точке Q₁ равно Х₁.

Рис.16. Эффект дохода и эффект замены по Хиксу.

Реальное увеличение потребления бананов в результате снижения их цены составит х₁ – х₀. Этот отрезок надо разделить на две части, чтобы показать, какая его часть связана с эффектом замены, а какая – с эффектом дохода.

Хикс определил, каким должен быть денежный доход потребителя, чтобы при изменившемся соотношении цен обеспечить ему прежний уровень удовлетворения. Для этого он строит вспомогательную бюджетную линию K₁L* (линия Хикса), которая параллельна новой бюджетной линии KL₁ и одновременно является касательной к исходной кривой безразличия i₀ в точке Q. Количество потребляемых бананов в точке Q₂ равно х₂. Поскольку K₁L* отражает новое соотношение цен и в то же время наборы фруктов Q₀ и Q₂ обеспечивают одинаковый уровень удовлетворения (находятся на одной и той же кривой безразличия i₀), то увеличение потребления бананов равное х₂-х₀, представляет собой эффект замены.

Переход от точки, так называемого, вспомогательного оптимума Q₂ к точке нового оптимума Q₁ означает рост потребления и бананов и яблок. При этом увеличение спроса на бананы происходит исключительно в силу роста реального дохода, поскольку оба оптимума (Q₂ и Q₁) характеризуются одинаковым соотношением цен товаров.

Подход Слуцкого к проблеме разложения общего эффекта изменения цены на эффект дохода и эффект замены существенно отличается от подхода Хикса (см. рис. 17).

Рис. 17. Эффект дохода и эффект замены по Слуцкому.

Слуцкий определяет, каким должен быть денежный доход потребителя, который обеспечил бы ему возможность приобретения после изменения цен тот же самый набор товаров, что и до их изменения. Для этого надо через точку Q₀ провести вспомогательную бюджетную линию K1L*(линия Слуцкого), параллельную новой бюджетной линии KL₁. Линия Слуцкого будет касательной к более высокой, чем i₀, кривой безразличия i* в точке Q_2. Поскольку Q₁ и Q₂ принадлежат одной бюджетной линии K₁L*, то реальный доход по Слуцкому остаётся неизменным. Но так как K₁L* параллельна KL₁, то она тоже отражает новое соотношение цен на бананы и яблоки. Следовательно, увеличение потребления бананов, равное х₂-х_0, и есть эффект замены.

Новая точка равновесия потребителя Q₁ принадлежит более высокой бюджетной линии, чем точка вспомогательного оптимума Q₂. Но, в то же время соотношение цен на бананы и яблоки в точках Q₁ и Q₂ одинаково. Значит, увеличение потребления бананов, равное х₁-х_2, и есть эффект дохода.

Если сравнить оба подхода к решению проблемы, можно сделать следующие выводы:

1. линия Слуцкого всегда выше линии Хикса, так как первая представляет собой секущую к исходной кривой безразличия, а линия Хикса – касательную к этой кривой. Поэтому эффект замены по Слуцкому всегда больше эффекта замены по Хиксу, а эффект дохода по Слуцкому всегда меньше эффекта дохода по Хиксу.

2. подход Хикса в большей степени соответствует основным положениям порядковой теории полезности, предполагает знание понятий предпочтений потребителя и кривых безразличия, тогда как подход Слуцкого не требует этого и позволяет дать количественное решение задачи на основе наблюдаемых фактов поведения покупателей на рынке.