ПЛАН

1. Повторення

2. Простір. Закони розміщення в просторі.

3. Розміщення елементів сайту по законах розміщення об’єктів.

4. Суб’єкт – об’єкт. Колірні схеми. Стилі веб-сайтів.

5. Види сайтів за призначенням. Мета сайту. Його структура.

6. Робота з замовником.

   1. Визначення мети сайту.

   2. Структура сайту.

   3. Структура сторінок сайту.

   4. Колірна схема.

7. Mock-up.

8. Остаточний дизайн.

Зміст

Розділ 1. Повторення

Розділ 2. Простір. Закони розміщення в просторі.

Тема 1. Правила розміщення в просторі

1. Золотий перетин або Золотий прямокутник

2. Числа Фібоначчі в дизайні.

3. П'ять елементів або Kundli дизайн

4. Коливання синусоїди

5. Правило Третин

Розділ 3. Розміщення елементів сайту по законах розміщення об’єктів.

Тема1. Модульна сітки.

1. Що таке модульна сітка?

2. Навіщо використовувати модульну сітку?

3. Як користуватися модульною сіткою?

4. Корисні ресурси

Розділ 4. Суб’єкт – об’єкт. Колірні схеми. Стилі веб-сайтів.

Тема 1. Основні елементи дизайну, які беруть участь у створенні композиції

1. Простір

2. Лінія

3. Фігура

4. Колір

5. Текстура

6. Форма

7. Світлотінь

8. Розмір

Тема 2. Психологія кольору і його вплив на емоційний стан

1. Червоний

2. Зелений

3. Оранжевий

4. Синій

5. Чорний

6. Білий

7. Фіолетовий

8. Жовтий

9. Коричневий

10. Рожевий

Тема 3. Поєднання кольорів для веб-сайтів

1. Колірні моделі

   1. Колірна модель RGB

   2. Компліментарна палітра

2. Палітри кольорів

   1. Монохроматична палітра

   2. Компліментарна палітра

   3. Спліт компліментарна палітра

   4. Аналогова палітра

   5. Класична палітра

   6. Прямокутна палітра

   7. Палітра квадрат

Тема 4. Стилі веб-сайтів

1. Стиль класика

2. Стиль web 2.0.

3. Стиль гранж

4. Стиль мінімалізм

Простір. Закони розміщення в просторі.

Простір – загальний «контейнер» для розміщення об’єктів. Простір буває одновимірний, двохвимірний, та багатовимірний. Ми будемо працювати з двовимірним та тривимірним просторами. 1.1. Золотий перетин або Золотий прямокутник

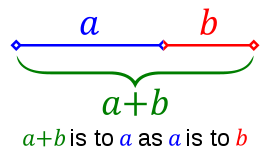Золотий перетин (золота пропорція, ділення в крайньому і середньому відношенні) - ділення безперервної величини на дві частини в такому відношенні, при якому менша частина так відноситься до більшої, як більша до всієї величини. Ставлення частин у цій пропорції виражається ірраціональною математичною константою, рівною приблизно 1.618033987.

Прийнято вважати, що об'єкти, що містять в собі «золотий перетин», сприймаються людьми як найбільш гармонійні.

Тепер перейдемо до Золотого прямокутнику. Тут все просто. У такого прямокутника довжини прилеглих сторін співвідносяться за правилом золотого перетину, тобто 1:1.618.

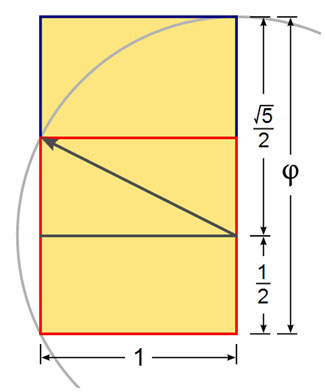Для того, щоб побудувати золотий прямокутник спочатку малюємо квадрат (червоний колір на картинці), потім проводимо лінію від середини однієї зі сторін квадрата до протилежного кутку (лінія зі стрілкою на малюнку). Використовуємо цю лінію як радіусу дуги, яка визначить висоту прямокутника. Тепер домальовували прямокутник (синій колір на малюнку).

Розглянемо в якості наочного прикладу цей мінімалістичний дизайн, представлений нижче. Він складається з 6 золотих прямокутників, розміром 299х185 пікселів, по 3 прямокутника в ряд. Сторони цим прямокутників співвідносяться за правилом золотого перетину 299/185 = 1,616.

Зверніть увагу на велику кількість простору навколо золотого прямокутника. Вона створює спокійну і приємну атмосферу. Незважаючи на використання всього декількох кольорів і однотипних блоків, всі елементи навігації інтуїтивно зрозумілі і служать своїй меті.

Для того, щоб додати новий блок не порушуючи при цьому логіку конструкції, найкращий варіант - додавати блоки третім рядом і рухатися подібним чином вниз.

Області застосування. Використання Золотих прямокутників в дизайні добре підходить для різних фото галерей, сайтів портфоліо і сайтів, орієнтованих на представлення продуктів.

1.2. Числа Фібоначчі в дизайні.

Числа Фібоначчі - це математична послідовність з ряду чисел. За визначенням, два перших числа Фібоначчі рівні 0 і 1. Кожне наступне число дорівнює сумі двох попередніх. Ряд чисел виглядає наступним чином: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...

Числа Фібоначчі використовують в музиці для настроювання інструментів, в архітектурі для обчислення гармонійних пропорцій, наприклад співвідношення висоти приміщення до висоти декорування стін різними матеріалами. Відстані між листям (або гілками) на стовбурі рослини відносяться приблизно як числа Фібоначчі.

Основна область застосування чисел Фібоначчі в дизайні - визначення розмірів блоків з основним контентом (контейнерів) і бічній панелі. Суть методу в наступному. Береться базова ширина контейнера, наприклад, 90 пікселів, і послідовно множиться на числа з ряду Фібоначчі. На підставі цих обчислень будується сітка сайту. Подивимося на прикладі.

Сторінка розділена на три колонки. Базова ширина контейнера 90 пікселів. Тоді перша колонка має ширину 180 пікселів (90 х 2), друга колонка має ширину 270 пікселів (90 х 3) і третя колонка має ширину 720 пікселів (90 х 8). Розмір шрифту також відповідає ряду Фібоначчі. Розмір шрифту в заголовку 55 пікселів, шрифт в розділі - 34 пікчеля і шрифт для тексту 21 піксель.

Якщо сайт має фіксовану ширину, наприклад 1000 пікселів, то числа Фібоначчі не дуже зручно використовувати. Остільки найближче до 1000 число з ряду Фібоначчі це 987 (..., 610, 987, 1597 ...), то саме з цього числа доведеться проводити обчислення для ширини блоків сайту. У таких ситуаціях найкраще скористатися правилом Золотого перетину (1000 х 0,618 = 618px) і виходячи з нього визначити ширину блоків.

Області застосування. Числа Фібоначчі найкраще підходять для дизайну блогів і журнальних макетів.

1.3. П'ять елементів або Kundli дизайн

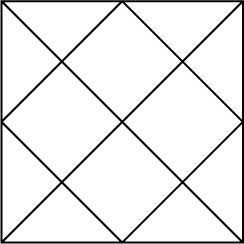Ще один цікавий приклад математики в дизайні - це техніка, заснована на правилах складання індійського гороскопу Kundli. Тут основою є наступна фігура. Вимальовується квадрат, всередині нього проводяться дві діагоналі, що сполучають протилежні кути, потім лініями з'єднуються центри сусідніх сторін квадрата.

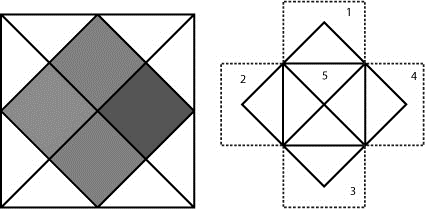
Усередині квадрата ми бачимо чотири ромба. Це і є основа для розташування п'яти елементів дизайну на сторінці.

Наведений нижче приклад дизайну сайту базується на геометрії Kundli. Цей макет може підійти для односторінкового сайту-візитка з елементами інтерактивного дизайну на основі jQuery технології.

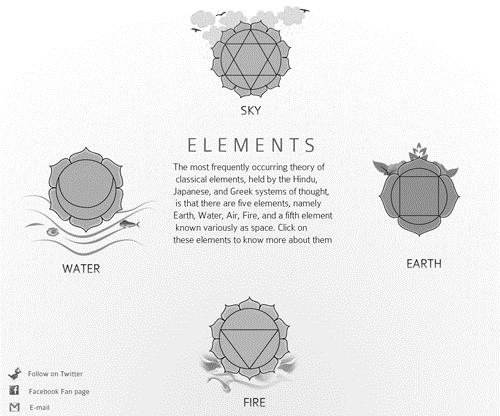
Також цей макет може легко перетворитися на сайт з трьохколонковою версткою хедером і футером.

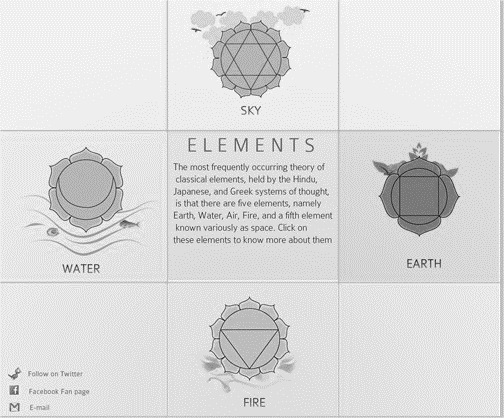
Області застосування. Ця конструкція найбільше підходить для сайтів портфоліо і сайтів, орієнтованих на демонстрацію продукції.

1.4. Коливання синусоїди

Якщо хочеться різноманітності, то зовсім не обов'язково дотримуватися базових правил золотого перетину і чисел Фібоначчі. Можна поекспериментувати і з іншими загальновідомими формулами.

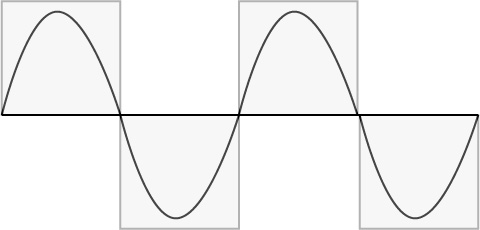
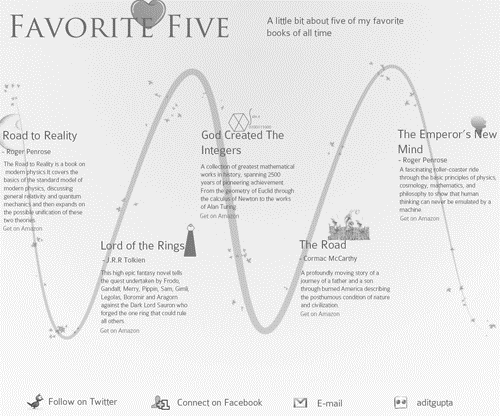Давайте подивимося яким вийде макет сайту, заснований на коливаннях синусоїди, математичної функції, яка описує повторювані коливання. На картинці нижче представлений приклад простого і оригінального односторінкового сайту.

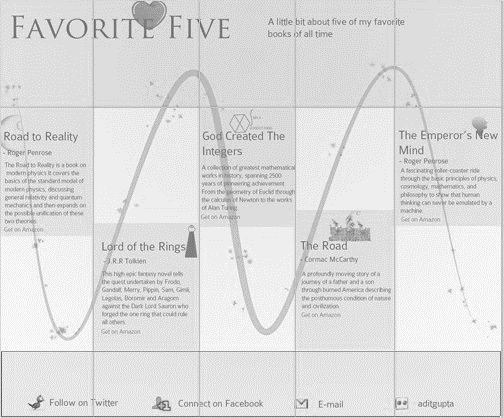Або ще один варіант. Макет, що складається з хедера, п'яти колонок і футера. Такий сайт також можна підсилити JQuery підказками, щоб зробити його більш інтерактивним.

Області застосування. Ця конструкція оптимальна для сайтів, де потрібна відображати хронологію подій. Найбільше підходить для горизонтальної навігації.