Вопросы и задачи для самоконтроля

1. Почему днищевые цистерны длинной стороной ориентированы вдоль судна?

2. Уменьшают ли вредное влияние свободной поверхности на начальную остойчивость днищевые стрингера, расположенные в цистерне?

3. Определить отрицательное влияние на метацентрическую высоту свободной поверхности забортной воды в балластном прямоугольном в плане танке, если его ширина 10,3 м, длина 25,8 м, плотность воды 1,022 т/м³, водоизмещение судна 9784 т.

4. Во сколько раз потребовалось бы увеличить поправку к метацентрической высоте на свободную поверхность жидкости после разрушения на танкере двух продольных переборок, проходящих на расстоянии 1/4 ширины судна от бортов?

5. Одинаково ли изменится остойчивость от появления свободной поверхности жидкости в цистерне на порожнем судне и на судне с полным грузом?

3.9 Плечо статической остойчивости на больших углах крена

При наклонениях судна на углы Θ > 10 ¸ 12⁰ и Ψ⁰ > 2 ¸ 3⁰ восстанавливающие моменты уже не могут быть определены по линейным метацентрическим формулам остойчивости. Для их определения используют уточенную теорию остойчивости. Уточненная теория остойчивости учитывает нелинейную зависимость восстанавливающего момента от угла наклонения, но сохраняет следующие из принятых в линейной теории допущения:

• наклонения судна равнообъемные;

• поперечные и продольные наклонения судна из исходного положения равновесия рассматриваются раздельно;

• в качестве мер остойчивости принимаются восстанавливающие моменты m_Θ , М_Ψ;

• предполагается, что в процессе наклонения судна ЦТ своего положения не меняет, а ЦВ перемещается в плоскости наклонения.

Однако по уточненной теории ряд допущений, принимаемых в разделе начальной остойчивости, прекращают свое действие. Так:

• осью наклонения уже не будет главная центральная ось x_f. Ось наклонения занимает произвольное положение, которое меняется с изменением угла наклонения;

• с изменением угла крена меняется площадь действующей ватерлинии, а значит ее момент инерции J_x и метацентрический радиус r являются переменными величинами . Поэтому ЦВ перемещается по кривой, не являющейся дугой окружности радиусом r;

• метацентр m´ не находится в диаметральной плоскости и его положение изменяется с изменением угла крена.

Для определения характеристик остойчивости судна на больших углах наклонения рассмотрим рис. 3.16.

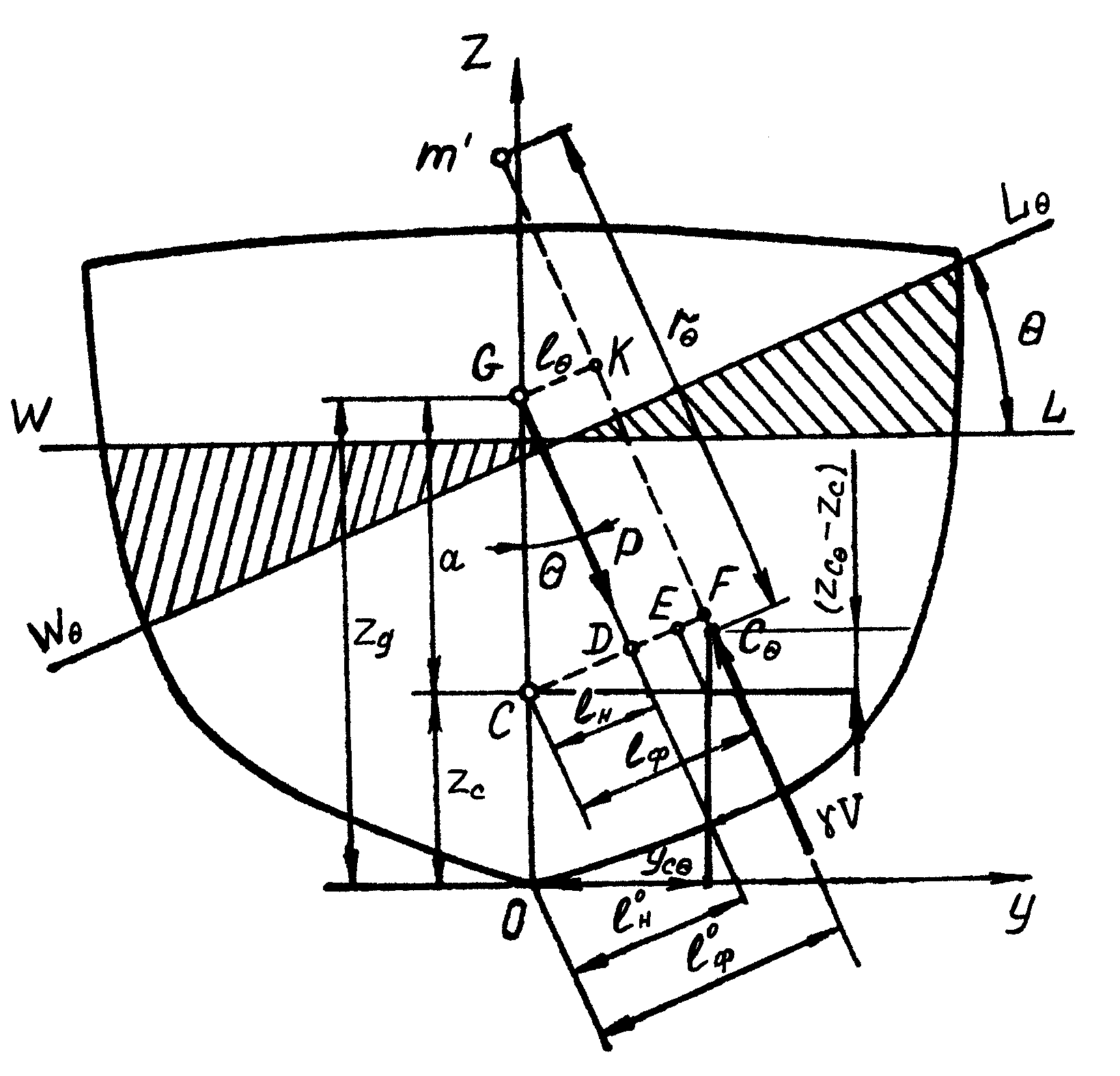
Рисунок 3.16 – Плечо статической остойчивости при больших углах крена

Как следует из рисунка, внешним силам, наклоняющим судно, противодействует восстанавливающий момент

m_Θ = γV l_Θ.

Из выражения видно, что плечо статической остойчивости l_Θ представляет собой поперечный восстанавливающий момент, приходящийся на единицу водоизмещения, что позволяет использовать ее в качестве меры остойчивости судна на больших углах наклонения.

Если из центра величины С опустить перпендикуляр на линию действия силы плавучести судна в его наклонном положении, то плечо остойчивости l_Θ можно представить как разность

l_Θ = l_ф – l_н.

Плечо остойчивости формы l_ф при данном водоизмещении судна и угле крена зависит только от координат центра величины С_Θ, определяемых формой погруженного объема судна:

l_ф = + = y_cΘ cosΘ + (z_cΘ – z_c) sinΘ.

Плечо остойчивости нагрузки l_н зависит только от возвышения ЦТ над ЦВ.

l_н = СD = (z_g – z_c) sinΘ = α sinΘ.

Соответственно момент m_ф = γVl_ф называют моментом остойчивости формы, а момент m_н = γV l_н – моментом остойчивости нагрузки.

Часто в качестве плеча остойчивости формы принимают длину перпендикуляра (рис. 3.16), опущенного на линию действия силы плавучести из начала координат. В этом случае его обозначают l⁰_ф и называют условным плечом остойчивости формы (или плечом формы относительно основной плоскости l_k ). Очевидно, что

l⁰_ф = l_ф + z_c sinΘ.

Соответственно условное плечо остойчивости нагрузки будет:

l ⁰_н = z_g sinΘ.

При этом плечо статической остойчивости определится зависимостью

l_Θ = l⁰_ф – l ⁰_н = l⁰_ф – z_g sinΘ.

Также, в судовой документации могут использоваться плечи формы относительно произвольного полюса и метацентра (табл.8.9).