Вопросы и задачи для самоконтроля

1. Дайте определение метацентрической высоты.

2. Сформулируйте условие начальной остойчивости судна.

3. Вычислите значения поперечной и продольной метацентрических высот прямоугольного понтона длиной 25,0 м, шириной 4,2 м при z_g = 2,0 м, d = 2,5 м (k = 1/12).

4. Определите значение поперечной метацентрической высоты горизонтально плавающего бревна диаметром 0,6 м и длиной 4м, если плотность древесины 0,5 т/м³, а воды − 1,0т/м³ .

3.3 Метацентрические формулы остойчивости и их практическое применение

Как было рассмотрено в п. 5.4, при наклонении судна, действует пара сил, момент которой характеризует степень остойчивости.

При малых равнообъемных наклонениях судна в поперечной плоскости (рис.3.3) (ЦВ перемещается в плоскости наклонения), поперечный востанавливающий момент m_Θ может быть представлен выражением

m_Θ = P = γV ,

где плечо момента = l_Θ называют плечом поперечной остойчивости.

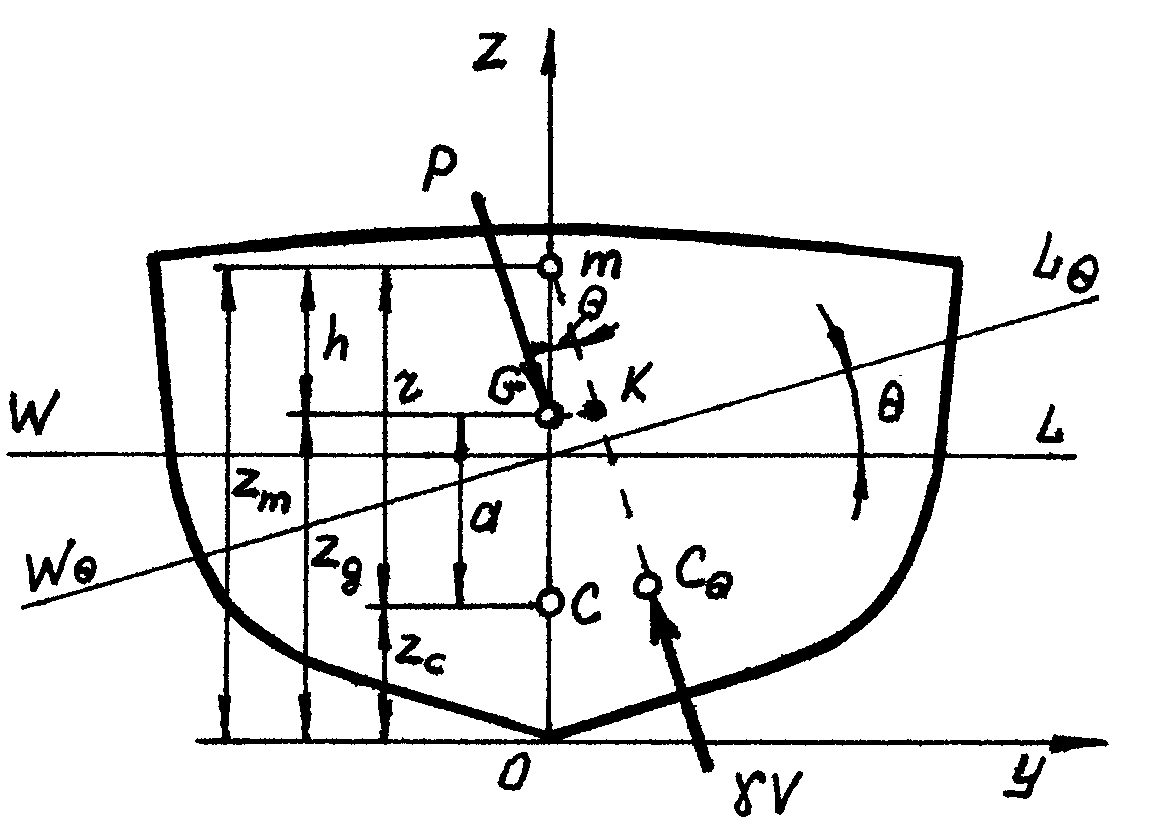
Рисунок 3.3 − Поперечное наклонение судна

Из прямоугольного треугольника mGK находим, что

l_Θ = h sinΘ.

Тогда m_Θ = P h sinΘ = γV h sinΘ.

Или учитывая малые значения Θ и принимая sinΘ Θ⁰/57,3⁰, получим метацентрическую формулу поперечной остойчивости:

m_Θ = γV h Θ⁰/57,3⁰.

Рассматривая по аналогии наклонения судна в продольной плоскости (рис.3.4), нетрудно получить метацентрическую формулу продольной остойчивости:

М_Ψ = P l _Ψ = γV Н sin Ψ = γV Н Ψ ⁰/57,3⁰,

где М_Ψ − продольный востанавливающий момент, а l _Ψ − плечо продольной остойчивости.

На практике используют коэффициент остойчивости, являющийся произведением водоизмещения на метацентрическую высоту.

Коэффициент поперечной остойчивости

К _Θ = γV h = Р h.

Коэффициент продольной остойчивости

К_Ψ = γV Н = Р Н.

С учетом коэффициентов остойчивости метацентрические формулы примут вид

m_Θ = К _Θ Θ⁰/57,3⁰,

М_Ψ = К_Ψ Ψ ⁰/57,3⁰.

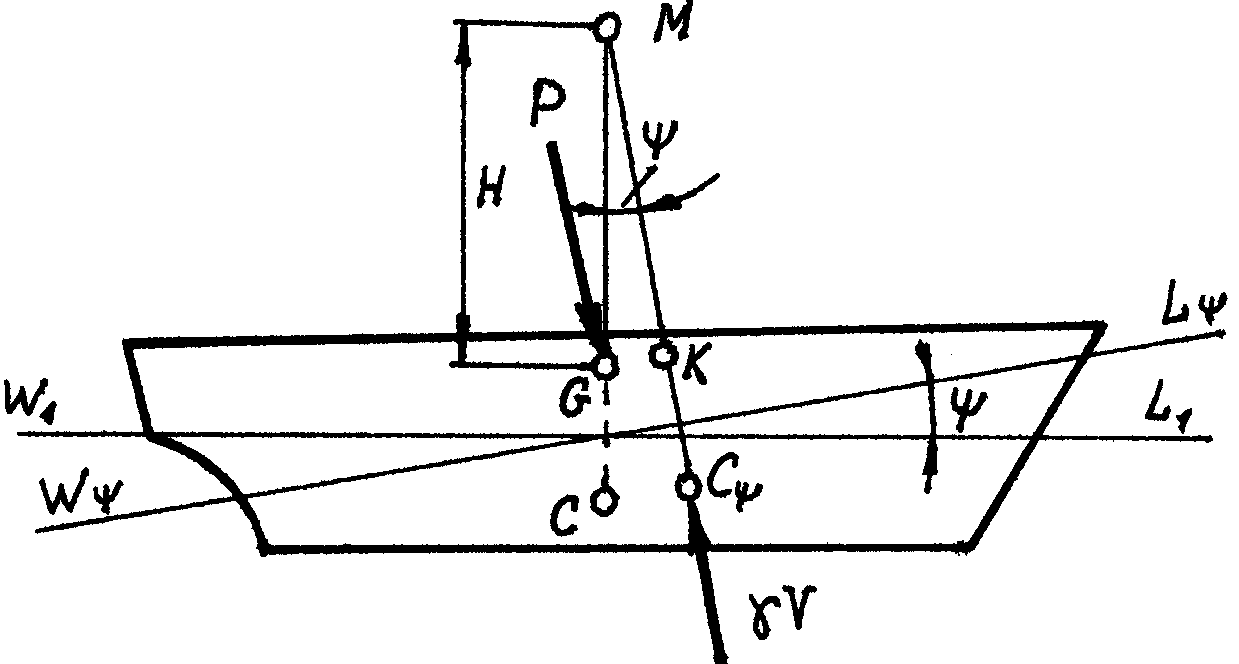
Рисунок 3.4 − Продольное наклонение судна

Метацентрические формулы остойчивости, дающие простую зависимость восстанавливающего момента от силы тяжести и угла наклонения судна, позволяют решать ряд практических задач, возникающих в судовых условиях. В частности, по этим формулам можно определить угол крена или угол дифферента, который получит судно от воздействия заданного кренящего или дифферентующего момента при известной массе и метацентрической высоте. Наклонение судна

под воздействием m_кр (М_диф) приводит к появлению обратного по знаку восстанавливающего момента m_Θ (М_Ψ), возрастающего по величине с нарастанием угла крена (дифферента). Нарастание угла крена

(дифферента) будет происходить до тех пор, пока восстанавливающий момент не станет равным по величине кренящему моменту (дифферентующему моменту), т.е. до выполнения условия:

m_Θ = m_кр и М_Ψ = М_диф.

После этого судно будет плавать с углами крена (дифферента):

Θ⁰ = 57,3⁰ m_кр /γV h ,

Ψ ⁰ = 57,3⁰ М_диф /γV Н.

Полагая в данных формулах Θ = 1⁰ и Ψ = 1⁰, найдем величины момента, кренящего судно на один градус, и момента, дифферентующего судно на один градус:

m₁⁰ = γV h = 0,0175 γV h,

М₁⁰ = γV Н= 0,0175 γV Н.

В ряде случаев используется также величина момента, дифферентующего судно на один сантиметр m_{Д .}При малом значении угла Ψ, когда tg Ψ Ψ, Ψ = (d_н – d_к)/L = D_f / L.

С учетом этого выражения метацентрическая формула для продольного восстанавливающего момента запишется в виде:

М_Ψ = М_диф = γV Н D_f / L.

Полагая в формуле D_f = 1 см = 0,01 м, получим:

m_Д = 0,01 γV Н/ L.

При известных значениях m₁⁰, М₁⁰ и m_Д, угол крена, угол дифферента и дифферент от воздействия на судно заданного кренящего или дифферентующего момента могут быть определены по простым зависимостям:

Θ⁰ = m_кр./ m₁⁰; Ψ⁰ = М_диф/ М₁⁰; D_f = М_диф/ 100 m_Д.

В приведенных выше рассуждениях предполагалось, что судно в исходном положении (до воздействия m_кр или М_диф) плавало прямо и на ровный киль. Если же в исходном положении судна крен и диф-

ферент отличались от нуля, то найденные значения Θ⁰, Ψ⁰ и D_f следует рассматривать как добавочные (δΘ⁰, δΨ ⁰ , δD_f ).

С помощью метацентрических формул остойчивости можно определить также, какой необходимый кренящий или дифферентующий момент надо приложить к судну, чтобы создать заданный угол

крена или угол дифферента (с целью заделки пробоины в бортовой обшивке, окраски или осмотра гребных винтов). Для судна, плавающего в исходном положении без крена и дифферента:

m_кр = γV h Θ⁰ /57,3⁰ = m₁⁰ Θ⁰;

М_диф = γV Н Ψ ⁰ /57,3⁰ = М₁⁰ Ψ ⁰ , или

М_диф = 100 D_f m_Д.

Практически метацентрическими формулами остойчивости допустимо пользоваться при малых углах наклонения (Θ < 10⁰ 12⁰ и Ψ < 5⁰) но при условии, что при этих углах не входит в воду верхняя палуба или не выходит из воды скула судна. Они справедливы также при условии, что восстанавливающие моменты m_Θ и М_Ψ противоположны по знаку моментам m_кр и М_диф, т.е. судно обладает положительной начальной остойчивостью.