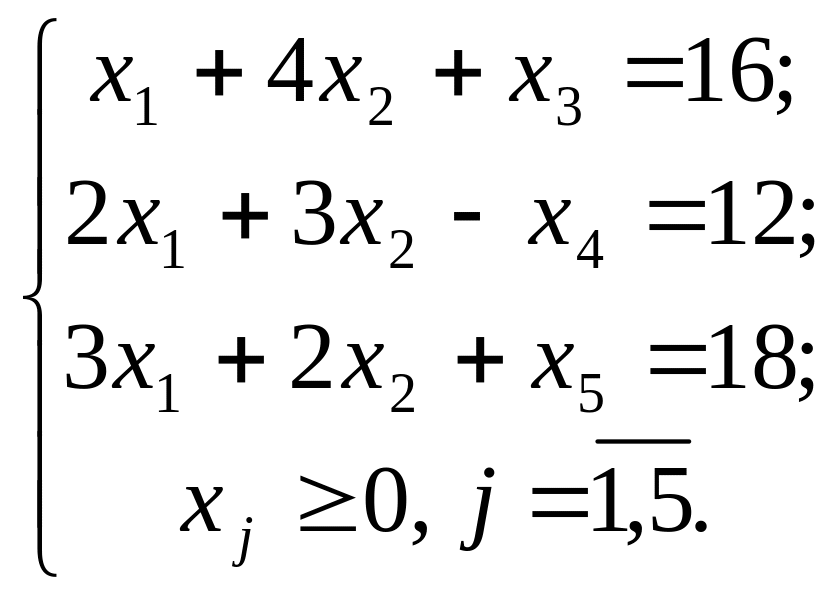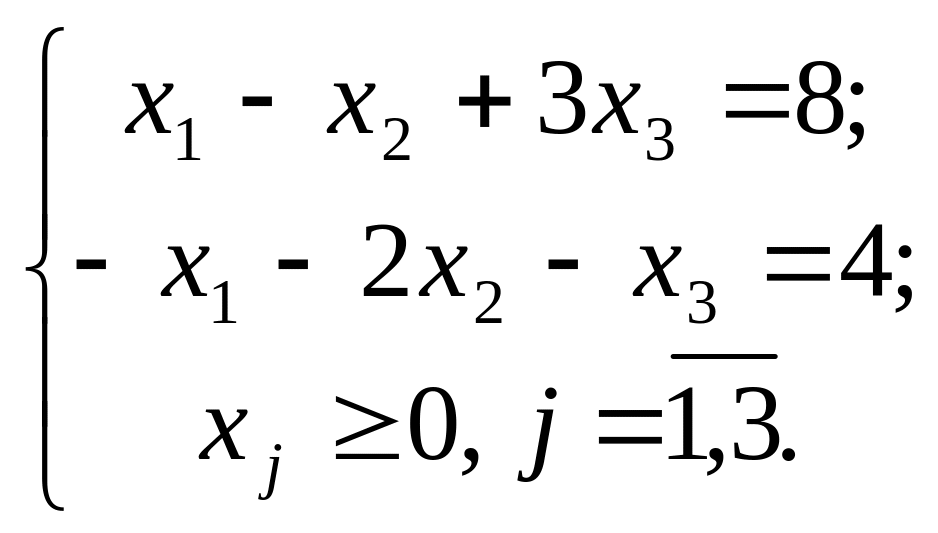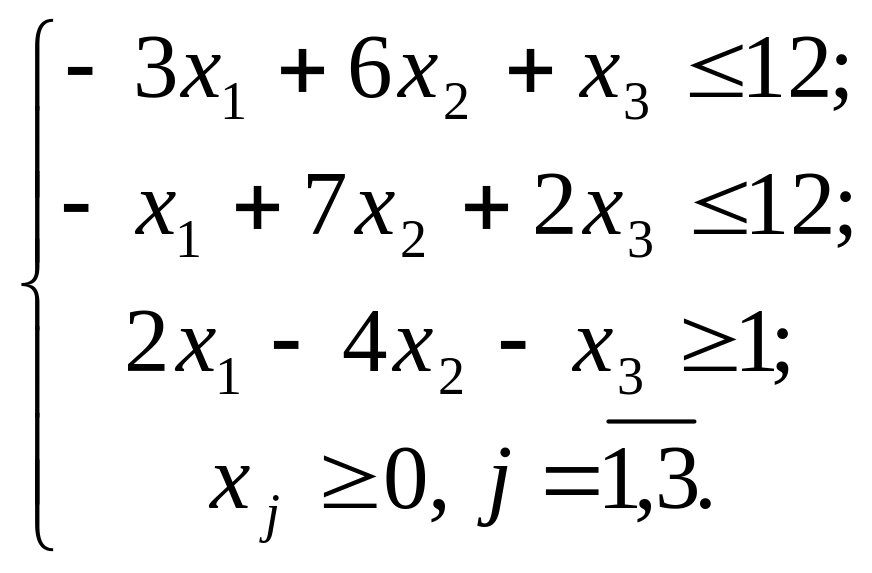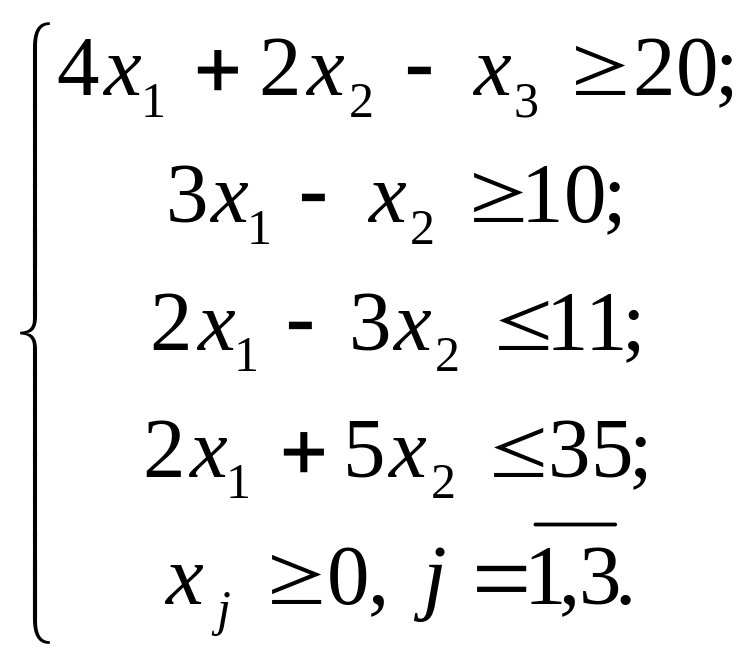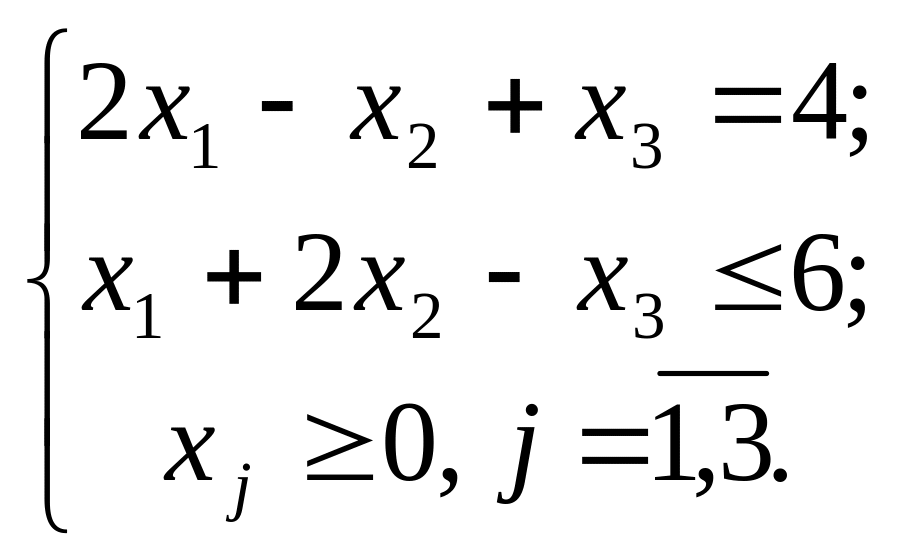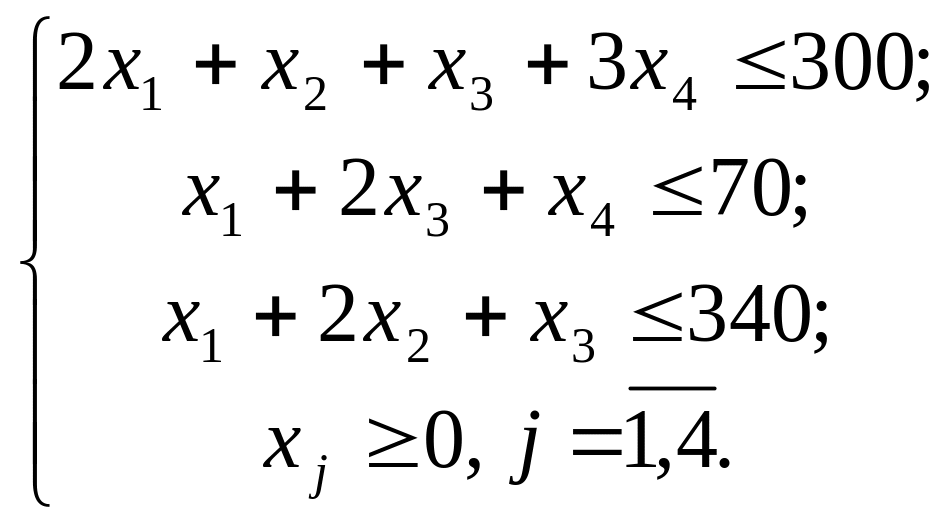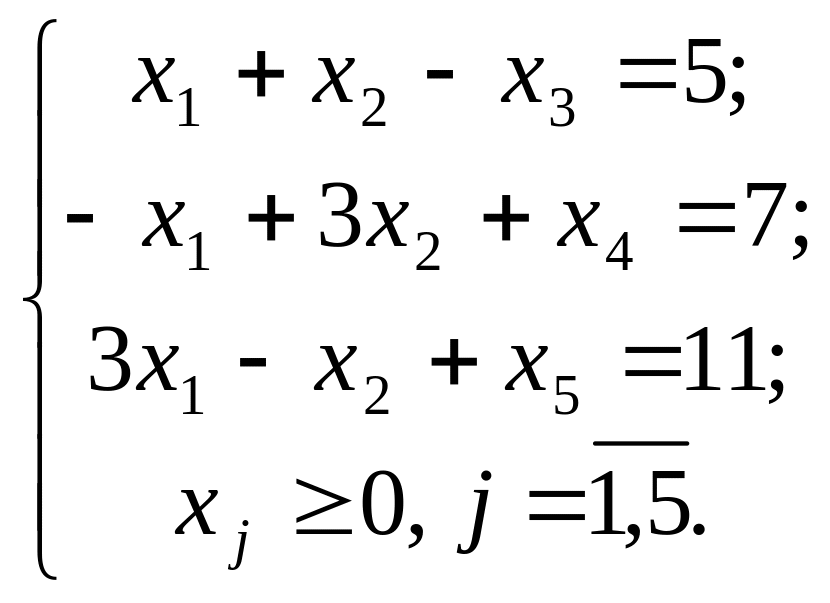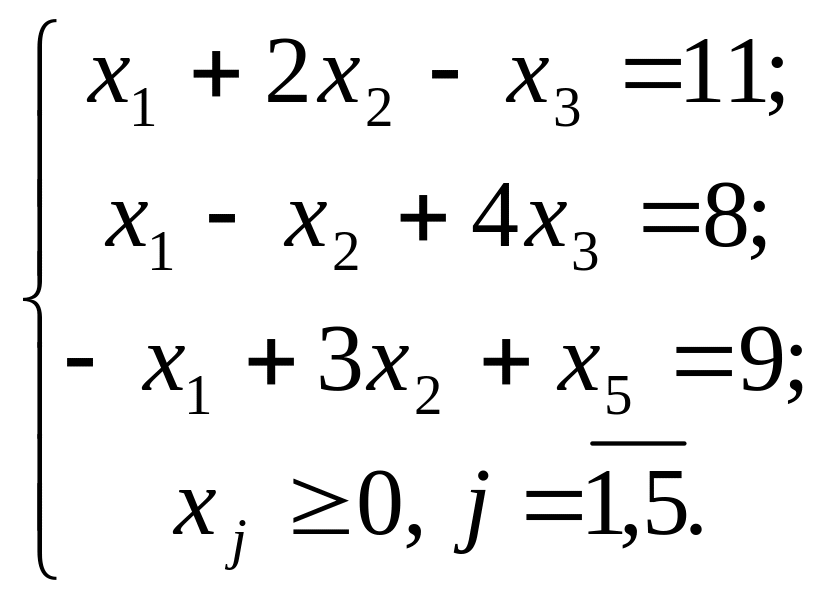Практична 5 Задачі дробово-лінійного програмування, деякі основні методи розв’язування та аналізу. Задачі нелінійного програмування, деякі основні методи розв’язування та аналізу
Розв’язати задачі дробово-лінійного програмування
Варіант
1.
за умов
|
Варіант
2.
за умов
|
Варіант
3.
за умов
|
Варіант
4.
за умов
|
Варіант
5.
за умов
|
Варіант
6.
за умов
|
Варіант
7.
за умов
|
Варіант
8.
за умов
|
Практична 6 Задачі динамічного програмування. Моделі та методи стохастичного програмування
Результати спостереження за нормами прибутку портфелів цінних паперів А і В подано в таблицях
Варіант 1
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
8 |
8 |
2 |
9 |
8 |
3 |
6 |
6 |
4 |
5 |
1 |
5 |
6 |
2 |
Варіант 2
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
6 |
2 |
2 |
5 |
4 |
3 |
7 |
5 |
4 |
5 |
8 |
5 |
2 |
2 |
Варіант 3
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
8 |
5 |
2 |
9 |
10 |
3 |
5 |
2 |
4 |
1 |
6 |
5 |
4 |
5 |
Варіант 4
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
2 |
7 |
2 |
1 |
4 |
3 |
8 |
7 |
4 |
2 |
3 |
5 |
7 |
5 |
Варіант 5
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
1 |
1 |
2 |
7 |
5 |
3 |
8 |
6 |
4 |
9 |
1 |
5 |
9 |
8 |
Варіант 6
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
4 |
8 |
2 |
2 |
5 |
3 |
6 |
6 |
4 |
2 |
8 |
5 |
7 |
2 |
Варіант 7
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
2 |
5 |
2 |
6 |
6 |
3 |
2 |
8 |
4 |
7 |
2 |
5 |
4 |
4 |
Варіант 8
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
5 |
8 |
2 |
7 |
1 |
3 |
6 |
6 |
4 |
2 |
1 |
5 |
6 |
8 |
Варіант 9
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
3 |
9 |
2 |
5 |
6 |
3 |
10 |
3 |
4 |
3 |
1 |
5 |
8 |
9 |
Варіант 10
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
2 |
2 |
2 |
5 |
7 |
3 |
5 |
2 |
4 |
4 |
3 |
5 |
7 |
1 |
Варіант 11
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
3 |
9 |
2 |
5 |
6 |
3 |
10 |
3 |
4 |
3 |
1 |
5 |
8 |
9 |
Варіант 12
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
1 |
2 |
2 |
4 |
5 |
3 |
9 |
5 |
4 |
1 |
4 |
5 |
5 |
7 |
Варіант 13
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
5 |
2 |
2 |
1 |
6 |
3 |
4 |
5 |
4 |
5 |
2 |
5 |
2 |
10 |
Варіант 14
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
2 |
1 |
2 |
3 |
4 |
3 |
10 |
9 |
4 |
2 |
0 |
5 |
5 |
5 |
Варіант 15
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
9 |
4 |
2 |
1 |
1 |
3 |
7 |
5 |
4 |
8 |
6 |
5 |
9 |
1 |
Варіант 16
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
6 |
3 |
2 |
5 |
7 |
3 |
2 |
2 |
4 |
10 |
9 |
5 |
4 |
45 |
Варіант 17
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
8 |
3 |
2 |
5 |
6 |
3 |
1 |
5 |
4 |
7 |
9 |
5 |
2 |
4 |
Варіант 18
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
5 |
8 |
2 |
2 |
1 |
3 |
4 |
9 |
4 |
8 |
7 |
5 |
2 |
6 |
Варіант 19
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
6 |
10 |
2 |
8 |
9 |
3 |
4 |
8 |
4 |
2 |
5 |
5 |
6 |
6 |
Варіант 20
Період |
Норма прибутку (%) |
|
ХА |
ХВ |
|
1 |
5 |
6 |
2 |
10 |
5 |
3 |
2 |
4 |
4 |
6 |
3 |
5 |
5 |
7 |
Визначити, який з цих проектів є менш ризикованим, виходячи з таких показників:
а) середньозважене модуля відхилення від центра групування, якщо в якості центра групування використовується його математичне сподівання;
б) дисперсія, середньоквадратичне відхилення;
в) коефіцієнт варіації
г) семіваріація, семіквадратичне відхилення;
д) коефіцієнт семіваріації;
е) коефіцієнт сподіваних збитків (задати своє значення Z)
є) коефіцієнт варіації асиметрії;
ж) коефіцієнт ексцесу.
Відповідь обґрунтуйте, поясніть можливі розбіжності в результатах
Завдання 2
а) обчислість коефіцієнт кореляції цінних паперів;
б) обчисліть сподівану норму прибутку та ризик портфеля цінних паперів, якщо акції А складають а% вартості портфеля;
в) обчисліть сподівану норму прибутку та ризик портфеля цінних паперів, якщо акції А складають b% вартості портфеля;
г) знайдіть портфель, який має мінімальний ризик;
д) визначте ступінь ризику цього портфеля;
е) знайдіть структуру портфеля, норма прибутку якого становила би с%;
ж) знайдіть структуру портфеля, ризик якого становила би d %. Обчисліть норму прибутку цього портфеля
Приклад
Результати спостереження за нормами прибутків портфелів цінних паперів А і В подано в таблиці:
Період |
Норма прибутку ( % ) |
|
хА |
хВ |
|
1 |
5 |
3,6 |
2 |
3 |
6 |
3 |
2 |
7,2 |
4 |
3 |
6 |
5 |
7 |
1,2 |
Визначити, який з цих проектів є менш ризикованим, виходячи з таких показників:
а) середньозважене модуля відхилення від центра групування, якщо в якості центра групування використовується його математичне сподівання;
б) середньозважене модуля відхилення від центра групування, якщо в якості центра групування використовується його мода;
в) дисперсія, середньоквадратичне відхилення;
г) коефіцієнт варіації;
д) семіваріація, семіквадратичне відхилення;
е) коефіцієнт семіваріації;
є) коефіцієнт сподіваних збитків (вважати, що Z=M(X) (одному з двох ) або задати інше значення);
ж) коефіцієнт асиметрії, коефіцієнт варіації асиметрії;
з) коефіцієнт ексцесу.
Відповіді обґрунтуйте Поясніть можливі розбіжності в результатах.
Розв'язання.
а) В якості величини ризику в абсолютному вираженні часто використовується міра розсіювання значень економічного показника відносно центра групування цих значень, в якості якого використовується математичне сподівання.
Нехай
-
випадкові величини, що відображають
можливі прибутки від реалізації проектів.
Знайдемо величини сподіваних прибутків.
Оскільки ми використовуємо статистичну
інформацію щодо минулого, сподівану
норму прибутку, її варіацію та семіваріацію
можна обчислити за формулами:
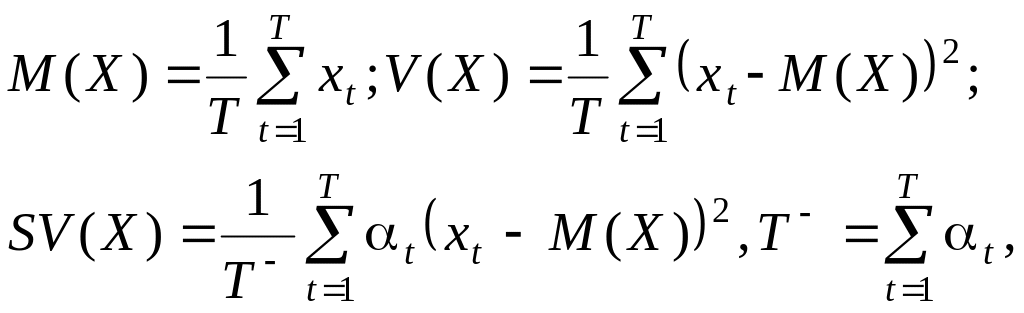
де
- випадкова величина норми прибутку за
попередні Т періодів, Т – кількість
періодів, які минули і в які здійснювались
спостереження за випадковою величиною.
Або ж можна вважати, що р1=р2=...=рТ=1/T.
Необхідні розрахунки приводяться в таблиці.
Для портфеля А:
i |
1 |
2 |
3 |
4 |
5 |
∑ |
хА=RA |
5 |
3 |
2 |
3 |
7 |
- |
p |
0,2 |
0,2 |
0,2 |
0,2 |
0,2 |
1 |
RAp |
1 |
0,6 |
0,4 |
0,6 |
1,4 |
4 |
(x-M(x)) |
1 |
-1 |
-2 |
-1 |
3 |
-- |
|
1 |
1 |
2 |
1 |
3 |
8 |
pIx-M(x)I |
0,2 |
0,2 |
0,4 |
0,2 |
0,6 |
1,6 |
(x-Mo) |
3 |
0 |
-1 |
0 |
4 |
-- |
|
3 |
0 |
1 |
0 |
4 |
8 |
p |
0,6 |
0 |
0,2 |
0 |
0,8 |
1,6 |
(x-M(x))2 |
1 |
1 |
4 |
1 |
9 |
-- |
p(x-M(x))2 |
0,2 |
0,2 |
0,8 |
0,2 |
1,8 |
3,2 |
α |
0 |
1 |
1 |
1 |
0 |
-- |
αp |
0 |
0,2 |
0,2 |
0,2 |
0 |
0,6 |
αp(x-M(x))2 |
0 |
0,2 |
0,4 |
0,2 |
0 |
1,2 |
(x-M(x))/σ(x) |
0,56 |
-0,56 |
-1,1 |
-0,56 |
1,67 |
-- |
((x-M(x))/σ(x))3 |
0,17 |
-0,17 |
-1,40 |
-0,17 |
4,72 |
-- |
((x-M(x))/σ(x))3p |
0,03 |
-0,03 |
-0,28 |
-0,03 |
0,94 |
0,63 |
((x-M(x))/σ(x))4 |
0,10 |
0,10 |
1,56 |
0,10 |
7,91 |
-- |
((x-M(x))/σ(x))4p |
0,02 |
0,02 |
0,31 |
0,02 |
1,58 |
1,95 |
Для портфеля В:
i |
1 |
2 |
3 |
4 |
5 |
∑ |
хВ=RВ |
3,6 |
6 |
7,2 |
6 |
1,2 |
- |
p |
0,2 |
0,2 |
0,2 |
0,2 |
0,2 |
1 |
RВp |
0,72 |
1,2 |
1,44 |
1,2 |
0,24 |
4,8 |
(x-M(x)) |
-1,2 |
1,2 |
2,4 |
1,2 |
-3,6 |
-- |
|
1,2 |
1,2 |
2,4 |
1,2 |
3,6 |
9,6 |
pIx-M(x)I |
0,24 |
0,24 |
0,48 |
0,24 |
0,72 |
1,92 |
(x-Mo) |
-2,4 |
0 |
1,2 |
0 |
-4,8 |
-- |
|
2,4 |
0 |
1,2 |
0 |
4,8 |
-- |
p |
0,48 |
0 |
0,24 |
0 |
0,96 |
1,68 |
(x-M(x))2 |
1,44 |
1,44 |
5,76 |
1,44 |
12,96 |
-- |
p(x-M(x))2 |
0,29 |
0,29 |
1,15 |
0,29 |
2,59 |
4,61 |
α |
1 |
0 |
0 |
0 |
1 |
-- |
αp |
0,2 |
0 |
0 |
0 |
0,2 |
0,4 |
αp(x-M(x))2 |
0,29 |
0 |
0 |
0 |
2,592 |
2,88 |
(x-M(x))/σ(x) |
-0,56 |
0,56 |
1,12 |
0,56 |
-1,68 |
-- |
((x-M(x))/σ(x))3 |
-0,17 |
0,17 |
1,40 |
0,17 |
-4,72 |
-- |
((x-M(x))/σ(x))3p |
-0,03 |
0,03 |
0,28 |
0,03 |
-0,94 |
-0,63 |
((x-M(x))/σ(x))4 |
0,10 |
0,10 |
1,56 |
0,10 |
7,91 |
-- |
((x-M(x))/σ(x))4p |
0,02 |
0,02 |
0,31 |
0,02 |
1,58 |
1,95 |
Оскільки, WA < WB , то виходячи з позицій мінімального ризику, для інвестора більш привабливішим є портфель А. А більші значення цієї оцінки для портфеля В свідчать про більшу нестабільність щодо цього портфеля .
б) Коли в якості центра групування використовують модальне значення показника, розрахунки аналогічні.
Знайдемо модальне значення показника для портфелів А і В( значення, яке зустрічається найчастіше ) :
Мо(ХА)=3; Мо(ХВ)=6.
Тоді
Оскільки WA > WB , то для інвестора більш привабливішим є портфель А.
в)
Оскільки WА-
< WB-
, то
портфель В
є більш ризикованим ніж портфель
А.Перевагу
слід надати портфелеві А.
Аналогічний результат ми отримаємо, якщо за міру ризику приймемо середньоквадратичне відхилення:
тобто, портфель А
є менш
ризикованим.
г) Для двох альтернативних портфелів А і В виявилося, що М+(ХА)<M+(XB),
-(XA)<-(XB), тому порівняння значень дисперсії дозволяє зробити висновок щодо ризикованості портфелів, але обґрунтований вибір портфеля для інвестування можна зробити лише розрахувавши відносні величини, які характеризуватимуть величину ризику, що припадає на одиницю доходу, тобто, коефіцієнти варіації.
Оскільки CV-(XA)=CV-(XB), то відповідь щодо вибору оптимального рішення дати неможливо.
е) А тому скористаємося критерієм мінімальної семіваріації або семіквадратичного відхилення.
Оскільки WA<WB, то для інвестора більш привабливим щодо інвестування є портфель А. Зроблений на основі критерію мінімальної семіваріації висновок підтверджує попередні результати.
Оскільки SSV-(XA)<SSV-(XB), то з позицій мінімального семіквадратичного відхилення ступінь ризику портфеля А, як і раніше, є меншим від ступеня ризику портфеля В.
е) Перевіримо правильність зроблених висновків, скориставшись критерієм мінімального коефіцієнта семіваріації.
CSV-(XA)<CSV-(XB). Даний результат тільки підтверджує попередні висновки про те, що портфель А є менш ризикованим ніж портфель В.
є) Для обчислення коефіцієнта сподіваних збитків, припустимо, що Z=M(XA),тобто ZA=M(XA)=4,5, ZB=M(XB)=4,5
|
Акція виду А |
∑ |
Акція виду В |
∑ |
||||||||
pi |
0,2 |
0,2 |
0,2 |
0,2 |
0,2 |
1 |
0,2 |
0,2 |
0,2 |
0,2 |
0,2 |
1 |
Xi |
5 |
3 |
2 |
3 |
7 |
- |
3,6 |
6 |
7,2 |
6 |
1,2 |
- |
Z |
4 |
4 |
4 |
4 |
4 |
- |
4 |
4 |
4 |
4 |
4 |
- |
-i |
0 |
1 |
1 |
1 |
0 |
- |
1 |
0 |
0 |
0 |
1 |
- |
I+ |
1 |
0 |
0 |
0 |
1 |
- |
0 |
1 |
1 |
1 |
0 |
- |
-ipi |
0 |
0,2 |
0,2 |
0,2 |
0 |
0,6 |
0,2 |
0 |
0 |
0 |
0,2 |
0,4 |
I+pi |
0,2 |
0 |
0 |
0 |
0,2 |
0,4 |
0 |
0,2 |
0,2 |
0,2 |
0 |
0,6 |
-ipiXi |
0 |
0,6 |
0,4 |
0,6 |
0 |
1,6 |
0,72 |
0 |
0 |
0 |
0,24 |
0,96 |
I+piXi |
1 |
0 |
0 |
0 |
1,4 |
2,4 |
0 |
1,2 |
1,44 |
1,2 |
0 |
3,84 |
Тоді
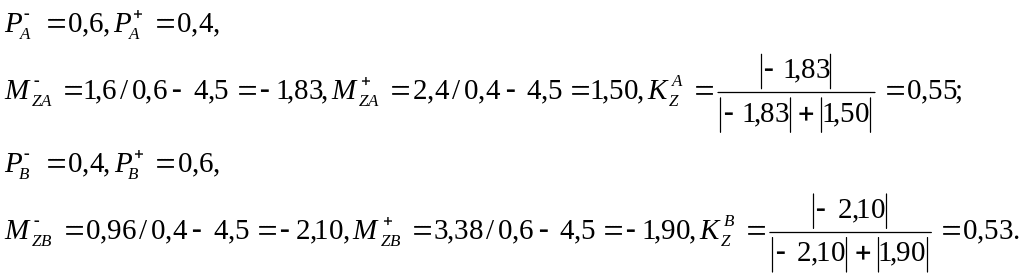
Оскільки К(XA) > К(XB) , то на основі коефіцієнта сподіваних збитків, який враховує запланований рівень прибутковості, ступінь ризику портфеля А є більшим, ніж у портфеля В
ж) У випадку асиметричного розподілу показників ефективності аналіз лише середньоквадратичного відхилення як міри ризик може бути недостатнім. Особливо, коли ці значення співпадають для кількох альтернативних об’єктів. У цьому випадку аналізують коефіцієнт асиметрії. Розглянемо на прикладі його обчислення.
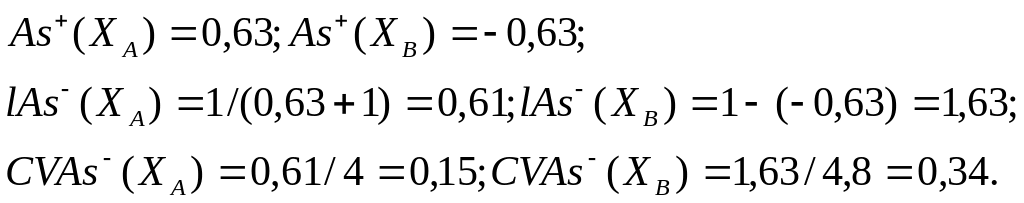
Виходячи з того, що As+(XA)>As+(XB),або lAs-(XA)<lAs-(XB), або CVAs-(XA)<CVAs-(XB), приходимо до висновку, що інвестиції слід робити в менш ризикований портфель А.
з)
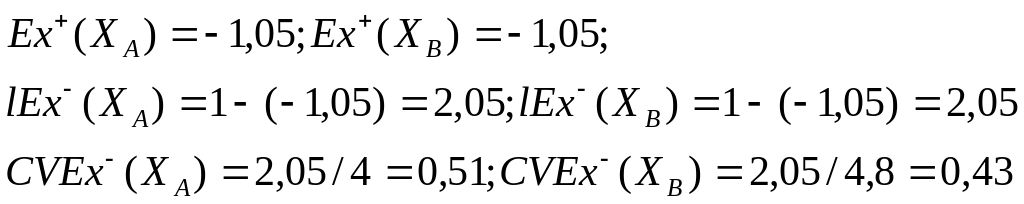
Згідно з розрахованими показниками Ex+(X) та lEx-(X) висновок про ризикованість об’єктів інвестування зробити не можна.
Проте
і на основі данного критерію
потрібно обрати варіант інвестування
В.
Якщо співставити висновки за усіма пунктами, то однозначного висновку про рівень ризику об’єктів інвестування зробити неможливо: за одними критеріями менш ризикованим є варіант А, за іншими В. Тому з огляду на висновки, сформульовані Г.Марковіцем варто розглянути можливість диверсифікації фінансових інвестицій.