Практична 4 Транспортна задача (тз): постановка, методи розв’язування та аналізу. Цілочислові задачі лінійного програмування: деякі з основних методів їх розв’язування та аналізу

_{Розв’язати транспортну задачу}

_{Варіант 1}

ai = (10; 20; 40); bj = (30; 10; 60);

.

_{Варіант 2}

ai = (30; 35; 60); bj = (25; 25; 40; 30);

.

_{Варіант 3}

ai = (160; 80; 60); bj = (60; 20; 40; 20; 100);

.

_{Варіант 4}

ai = (5; 20; 10); bj = (10; 25; 15);

.

_{Варіант 5}

ai = (30; 40; 20); bj = (40; 30; 20; 40);

.

_{Варіант 6}

ai = (30; 40; 50); bj = (35; 30; 60);

.

_{Варіант 7}

ai = (10; 20; 80; 50); bj = (30; 10; 60; 50);

.

_{Варіант 8}

ai = (40; 20; 50; 20); bj = (20; 45; 35; 40);

.

_{Приклад}

_{Підприємство має три філії А1, А2, А3, які можуть виготовляти відповідно 30, 20 та 15 тис. одиниць продукції на місяць. Укладено договори з чотирма замовниками B1, B2, B3, B4 на поставку продукції в кількості відповідно 10, 20, 25 та 20 тис. штук. Витрати на виробництво та транспортування тисячі одиниць продукції замовникам із кожної філії наведено в таблиці:}

_{Таблиця 6}

Витрати на виробництво та транспортування

Філія	В1	В2	В3	В4
А1	4	5	3	7
А2	7	6	2	5
А3	2	3	9	8

_{Визначити оптимальний план перевезення продукції до замовників, щоб загальна вартість виробництва і транспортування була мінімальною.}

_{Розв’язання}

_{Задача є незбалансованою, оскільки сумарний попит становить 75 тис. шт., а загальна пропозиція – 65 тис. шт. Тому потрібне введення додаткового фіктивного виробника (A4) з пропозицією 10 тис. одиниць продукції (75-65). Вважаємо, що вартість виробництва і транспортування від нього до кожного замовника дорівнює 0.}

_{Виконуємо в Excel таблицю з умови задачі, додаємо підприємство A4. У рядочок знизу вводимо значення попиту кожного замовника, у стовпчик справа – пропозиції філій.}

_{Оскільки маємо 4 виробника та 4 замовника, виділяємо нижче масив 4х4 (B11:E14), який буде містити оптимальний план задачі.}

_{У чарунку B15 вставляємо формулу =СУММ(B11:B14) і протягуємо її до E15. У F 11 вводимо = СУММ(B11:E11) і продовжуємо до F14.}

_{Чарунка F15 буде містити цільову функцію, вводимо в неї формулу =СУММПРОИЗВ(B4:E7;B11:E14).}

_{Обираємо в меню «Данные→Поиск решения». Встановлюємо цільову чарунку $F$15, що прямує до мінімуму. Вводимо обмеження $B$11:$E$14>=0; $B$15:$E$15$=B$8:$E$8; $F$11:$F$14=$F$4:$F$7.}

_{Натискаємо «Выполнить».}

_{Як бачимо, філія A1 має продати 10 тис. одиниць продукції замовнику B1, 5 тис. – B2 і 15 тис. – B3. Філія A2 постачатиме по 10 тис. шт. продукції підприємствам B3 та B4, а A3 – 15 тис. шт. підприємству B2. Частина попиту замовника B4 (10 тис. шт.) залишиться незадоволеною.}
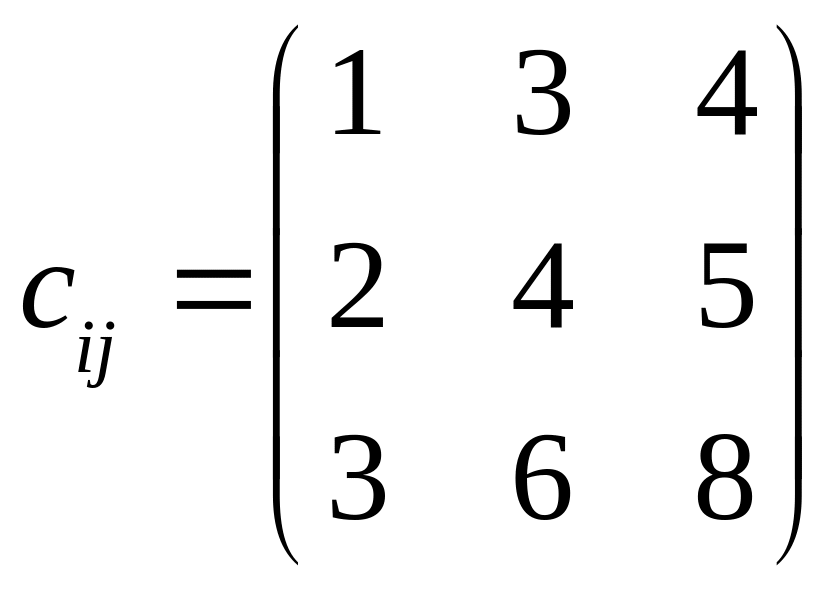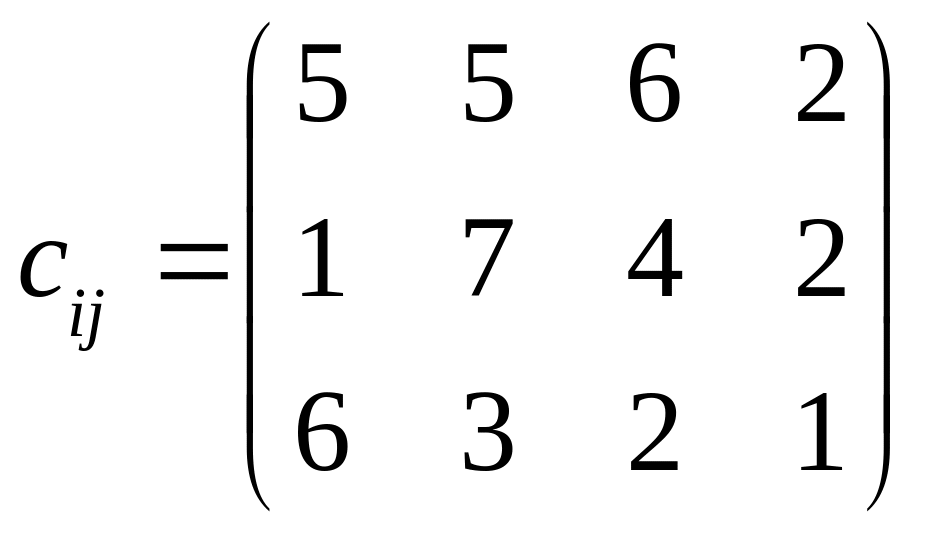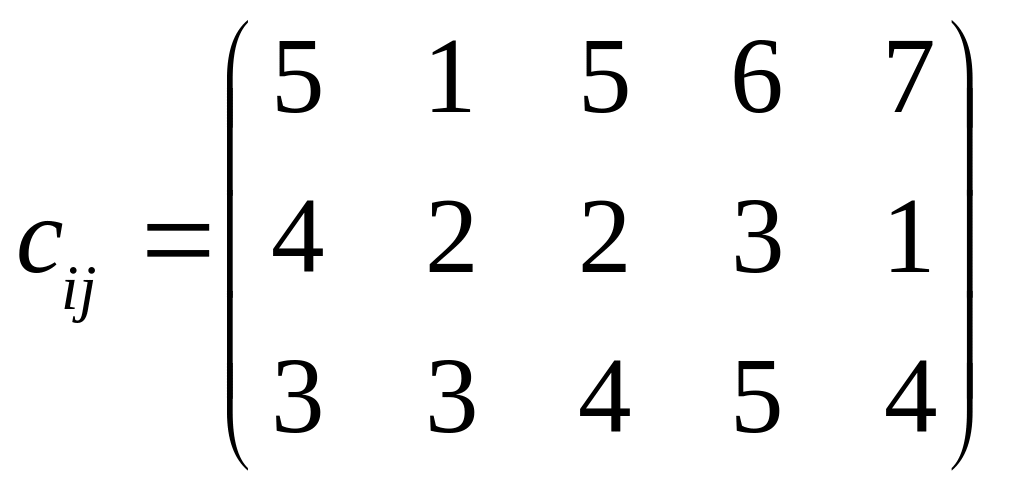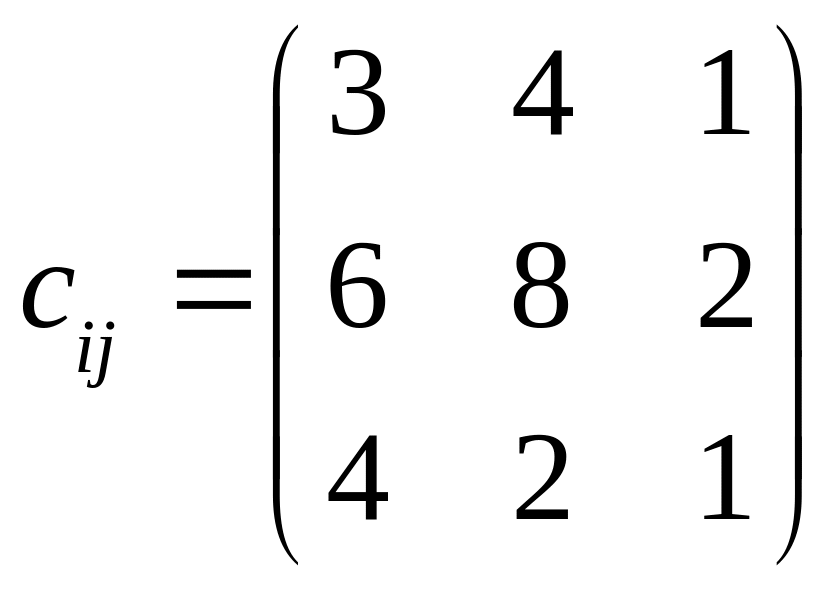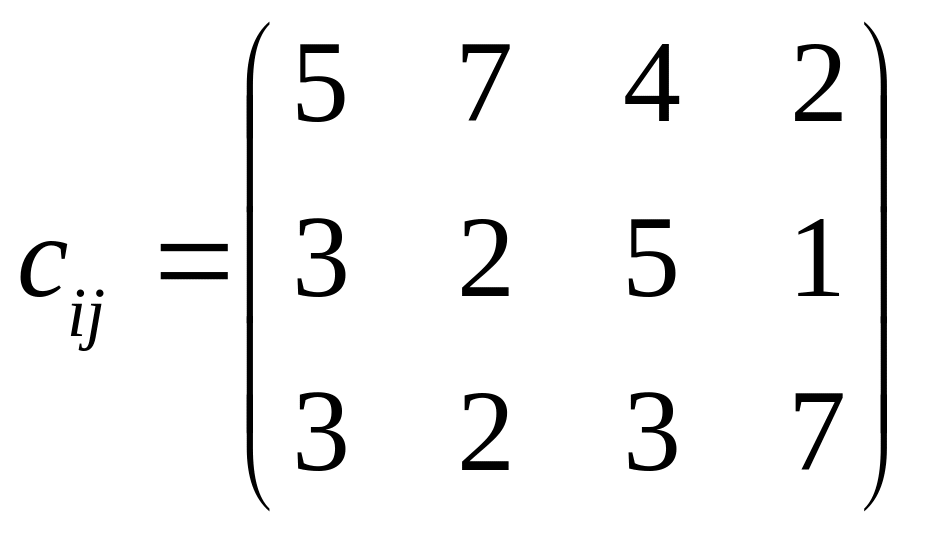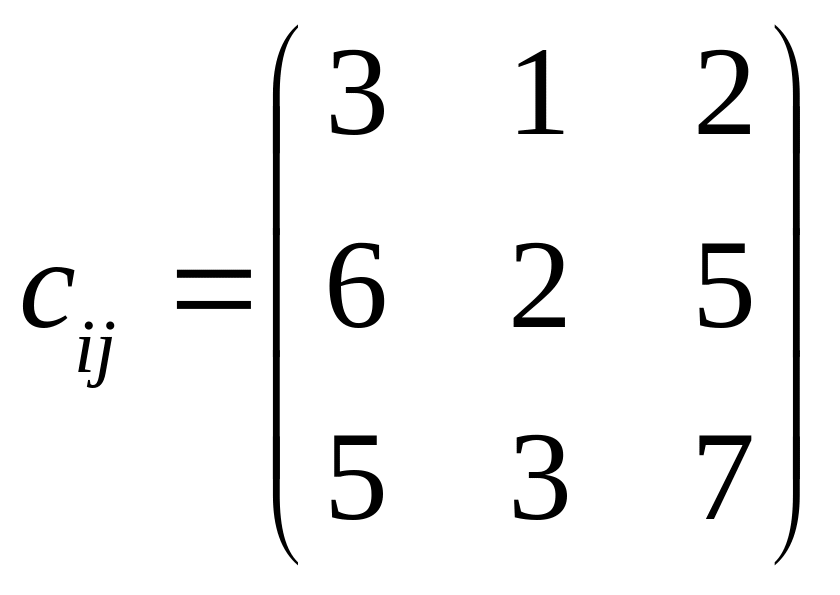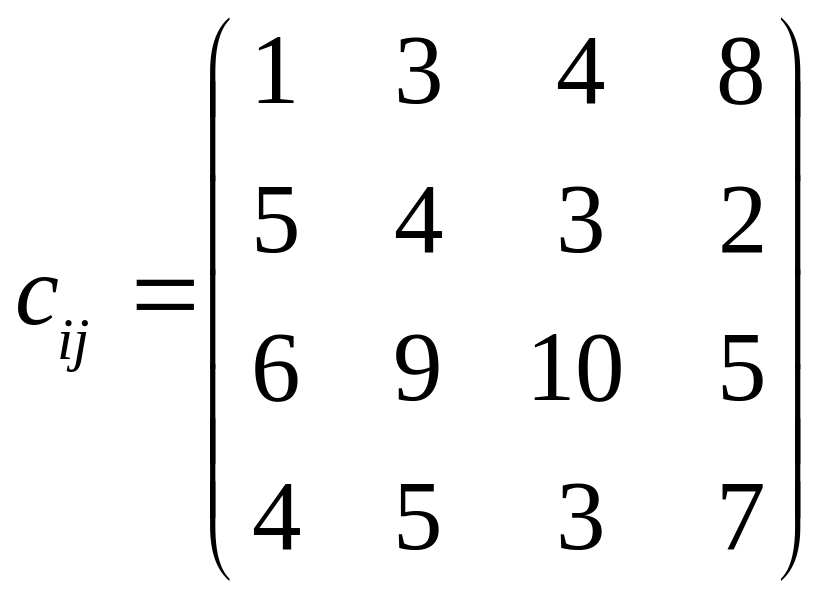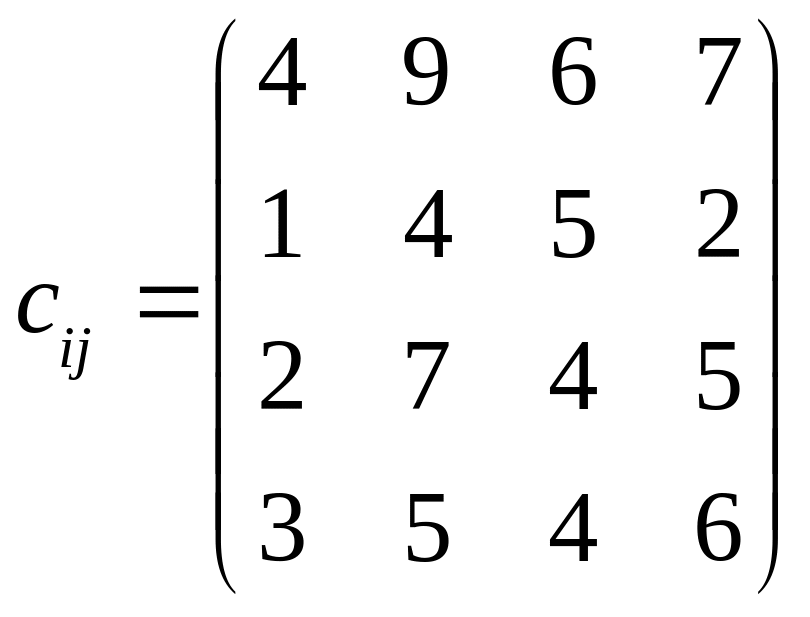