Объёмный (алфавитный) подход.

Алфавитный подход основан на том, что всякое сообщение можно закодировать с помощью конечной последовательности символов некоторого алфавита. Носителями информации являются любые последовательности символов, которые хранятся, передаются и обрабатываются с помощью компьютера. Алфавитный (объёмный) подход применяется в технике. Этот подход основан на подсчёте числа символов в сообщении, то есть связан только с длиной сообщения и не учитывает его содержания. При этом учитывается, так называемая, мощность алфавита – полное количество символов в алфавите (с учётом пробела, точки, запятой, тире, вопросительного и восклицательного знаков). Например, мощность русского алфавита складываемая из количества букв и перечисленных символов, равна: N =33+6=39.

В вычислительной технике битом называют наименьшую «порцию» памяти компьютера, необходимую для хранения одного из двух знаков: "0" или"1", используемых для внутримашинного представления данных и команд.

Для того чтобы закодировать алфавит из N символов, нужно взять i–разрядный код, определяемый из формулы:

Пример 3: Посчитать количество разрядов двоичного кода, необходимых для кодирования алфавита русского языка.

Решение: Так как мощность алфавита русского языка N=39, то 39 = 2ⁱ. Так как, 2⁵=32, 32<39, то ближайшая к 39 целая степень двойки: 39 < 2⁶=64. Оставшийся резерв можно использовать для кодирования цифр, всевозможных математических знаков, скобок и т.п.

Следовательно, i= 6.

Ответ: Количество двоичных разрядов для кодирования символов русского алфавита равно 6.

Длина i двоичного кода, с помощью которого кодируется символ алфавита, называется информационным весом символа.

Если - информационный вес символа алфавита, а – количество символов в тексте, записанном с помощью этого алфавита, то информационный объём текста выражается формулой:

(бит)

Так текст, состоящий из 1000 символов русского алфавита с мощностью N=39, равен I = 1000 6=6000 бит. Определите информационный вес символа алфавита, включающего в себя все строчные и прописные русские буквы (66), цифры (10), знаки препинания, скобки, кавычки (10).

Бит слишком мелкая единица измерения. На практике чаще применяется более крупная единица— байт, равная восьми битам.

1 байт= 8 бит

Например, именно восемь бит требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=2⁸). Информационный объём текста в памяти компьютера измеряется в байтах и равен количеству символов в записи текста.

Помимо бита и байта, для измерения информации используются и более крупные единицы:

1 Кб (килобайт) =	210 байт =	1024 байт
1 Мб (мегабайт) =	210 Кб =	1024 Кб
1 Гб (гигабайт) =	210 Мб =	1024 Мб
1 Тб (терабайт) =	210 Гб =	1024 Гб

4. Представление информации в двоичной системе счисления. Универсальность дискретного (цифрового) представления информации.

Мы уже с вами говорили, что компьютер может хранить и обрабатывать данные, представляющие информацию четырёх видов: числовую, текстовую, графическую и звуковую. Вне зависимости от вида информация в компьютере хранится, обрабатывается в виде двоичных кодов. В этом состоит универсальность представления информации. Также можно сказать, что представление данных в компьютере дискретно (от лат discretus — разделённый, прерывистый — свойство, противопоставляемое непрерывности).

К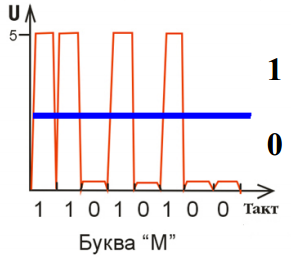 одирование и передача информации в компьютере осуществляется с помощью электрических сигналов. Обработка этих сигналов происходит в микросхемах. Уровню напряжения от 0 до 0,5 В (Вольт) условно поставлена в соответствие цифра 0, а уровню напряжения от 2,5 до 5 В – цифра 1. Информация, закодированная в виде двоичного кода, может быть представлена в виде цепочки электрических импульсов – кодом из восьми нулей и единиц. Например, на картинке изображён код буквы М – 11010100. Двоичную систему удобно использовать в компьютере, так как существующие технические устройства могут надёжно сохранять и распознавать два различных состояния: есть ток в элементе – 1, нет тока – 0.

Такое дискретное представление информации в виде двоичных кодов называют ещё цифровым.