1.Алгоритми на графах. Пошук в ширину і глибину

1.1 Представлення графів.

Є два стандартних способа представлення графу G = (V, Е) - як набір списків суміжних вершин або як матрицю суміжності. Перший зазвичай переважніше, бо дає більш компактне представлення для розріджених (sparse) графів - тих, у яких |Е| багато менше |V|². В деяких ситуаціях зручніше користуватися матрицею суміжності - наприклад, для щільних (dense) графів, у яких |Е| порівнянно з |V|². Матриця суміжності дозволяє швидко визначити, чи сполучені дві дані вершини ребром.

Подання графа G = (V, Е) у вигляді списків суміжних вершин (adjancency-list representation) використовує масив Adj з |V| списків - по одному на вершину. Для кожної вершини u £ V список суміжних вершин Adj [u] містить в довільному порядку всі суміжні з нею вершини.

Для орієнтованого графа сума довжин усіх списків суміжних вершин дорівнює загальному числу ребер: ребру (u, v) відповідає елемент v списку Adj [u]. Для неорієнтованого графа ця сума дорівнює подвоєному числу ребер, так як ребро (u, v) породжує елемент у списку суміжних вершин як для вершини u, так і для v. В обох випадках кількість необхідної пам'яті є O (max (V, E)) = O (V + E).

Списки суміжних вершин зручні для зберігання графів з вагою (weighted graphs), в яких кожному ребру приписана певна речовинна вага (weight), тобто задана вагова функція (weight function) w: Е - > R. У цьому випадку зручно зберігати вагу w (u, v) ребра (u, v) £ Е разом з вершиною v у списку вершин, суміжних з u. Подібним чином можна зберігати іншу інформацію, пов'язану з графом.

Недолік цього подання такий: якщо ми хочемо дізнатися, чи є в графі ребро з u в v, доводиться переглядати весь список Adj [u] в пошуках v. Цього можна уникнути, представивши граф у вигляді матриці суміжності - але тоді буде потрібно більше пам'яті.

При використанні матриці суміжності ми нумеруємо вершини графа (V, Е) числами 1,2, ..., |V| і розглядаємо матрицю А = (aij) розміру |V| x |V|, для якої :

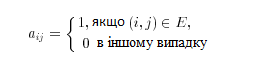
Для неорієнтованого графа матриця суміжності симетрична щодо головної діагоналі, оскільки (u, v) та (v, u) - це одне і те ж ребро. Іншими словами, матриця суміжності неорієнтованого графа збігається зі своєю транспонованою (transpose). (Транспонированием називається перехід від матриці А = (aij) до матриці Аᵗ = (aᵗfj), для якої aᵗij = aji). Завдяки симетрії достатньо зберігати тільки числа на головній діагоналі та вище неї, тим самим ми скорочуємо необхідну пам'ять майже вдвічі.

Як і для списків суміжних вершин, зберігання ваги не складає проблеми: вага w (u, v) ребра (u, v) можна зберігати в матриці на перетині u рядка та v стовпця. Для відсутніх ребер можна записати спеціальне значення NIL (в деяких завданнях замість цього пишуть 0 або∞).

Для невеликих графів, коли місця в пам'яті достатньо, матриця суміжності буває зручніше - з нею часто простіше працювати. Крім того, якщо не треба зберігати вагу, то елементи матриці суміжності представляють собою біти, які можна розміщувати в одному машинному слові, що дає помітну економію пам'яті.