Лекция 1 Основные понятия OpenGl

OpenGL – графический стандарт - разработан и утверждён ведущими компьютерными и программистскими фирмами (IBM, Microsoft и др.)

1.2 Однородные координаты и матрицы

В компьютерной графике вершины задаются четырьмя координатами, что связано с использованием однородных координат. Использование этих координат позволяет привести все виды пространственных преобразований графических объектов к единой форме. (К матричным преобразованиям.)

В однородной системе координат положение точки P(x,y,z) задаётся, как P(wx,wy,wz,w) или P(x,y,z,1). Где w – задаёт масштаб.

Переход из одной ортогональной системы координат к другой, как известно, задаётся системой

(1)

где α_i, β_i, γ_i, λ_i – некоторые заданные коэффициенты.

Уравнение (1) можно рассматривать не только, как положение точки в новой системе координат, но и как изменение положения точки в своей системе координат.

Любое преобразование, задаваемое системой (1), можно разложить на последовательно выполняемые простейшие преобразования:

- вращения (rotate) [R];

- растяжения (scale) [S];

- переноса (translate) [T].

Рассмотрим эти преобразования.

Перенос [T] . Вектор переноса (λ,μ,ν)

. В OpenGL glTranslatef(λ,μ,ν);

Растяжение [S].

. В OpenGL glScalef(α,β,γ);

В этих операторах префикс gl говорит об принадлежности этих операторов к библиотеки OpenGL, а суффикс f – говорит о том, что все параметры задаются в формате вещественных чисел (glFloat).

Вращение [R].

Рассмотрим, вначале, поворот точки вокруг оси z на угол φ

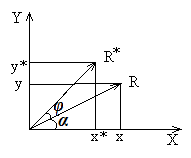
Эти уравнения получены с.о.

Матрица поворота вокруг оси аппликат (z) имеет вид

В OpenGL GlRotetef(φ,0,0,1);

Матрица поворота вокруг оси абсцисс (x) имеет вид

В OpenGL GlRotetef(φ,1,0,0);

Матрица поворота вокруг оси ординат (y) имеет вид

В OpenGL GlRotetef(φ,0,1,0);

1.3 Поворот точки вокруг прямой заданной точкой а(a,b,c) и направляющим вектором e(l,m,n), , на угол φ.

Поворот точки относительно оси можно реализовать последовательностью следующих операций:

1. Перенос точки А в начало координат

2. Совмещение прямой с одной из осей координат

3. Поворот на заданный угол φ вокруг этой оси

4. Вернуть прямую в прежнее положение

5. Вернуть точку А в исходное положение

Это преобразование можно записать в виде матрицы

[M] = [T] [Rx] [Ry] [Rz] [Ry]^-1 [Rx] ^-1[T] ^-1 (1)

Для случая прохождения линии через начало координат, матрица поворота точки вокруг линии заданной направляющим вектором на угол φ имеет вид

Для того, что бы воспользоваться операторами OpenGL, необходимо определить угол ψ поворота системы координат вокруг оси y и угол χ поворота вокруг оси x

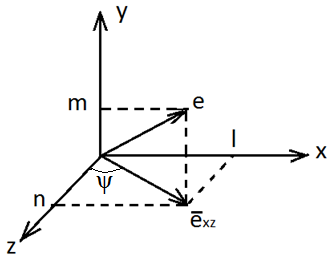–направляющмй вектор

.

Аналогичным образом находим угол χ

В OpenGl получить результирующую матрицу преобразования

[M] = [T] [Rx] [Ry] [Rz] [Ry]^-1 [Rx] ^-1[T] ^-1

можно с.о.

glPushMatrix

glTranslatef(-a,-b,-c);

glRotetef(ψ,0,1,0);

glRotetef(χ,1,0,0);

glRotetef(φ,0,0,1);

glRotetef(-χ,1,0,0);

glRotetef(-ψ,0,1,0);

glTranslatef(a-b,c);

glPopMatrix