2. Обґрунтування розрахункових залежностей до визначення напружень та деформацій за безмоментною теорією оболонок

За межами кріплення, що защемляє оболонку, вплив згинаючих моментів на напружено – деформований стан оболонки невеликий. Тому для цієї частини оболонки напруження та деформації можна рахувати за безмоментною теорією. Для циліндричної оболонки, яка вільно розширюється в осьовому напрямку, відсутні меридіональні напруження, тобто 0, а в окружному вони визначаються за залежністю [2]

. (1)

Перевірку міцності циліндричної оболонки звичайно виконують за _t , що визначається за формулою (1), яку часто називають “котельною” формулою [2]. Оскільки інерційне навантаження визначається лінійною залежністю при , тому тангенціальні напруження у закріпленні і в центрі оболонки визначаються відповідно за формулами

; . (2)

У цієї формулі – інтенсивність сил інерції оболонки; – інтенсивність сил інерції лопаток;  – щільність матеріалу ротора; m₀ – маса лопатки у центральної частині ротора; z – число лопаток в одному ступені; – радіус центру ваги лопатки; – ширина ступеня.

Деформацію оболонки w за безмоментною теорією можна визначити, користуючись узагальненим законом Гука для плоского напруженого стану.

(3)

Визначимо зв’язок між абсолютною зміною радіуса w (рис. 3) та відносною деформацією _t для виділеного кутового сектора :

Рис.3

Рис.3

. (4)

Зрівнюючи праві частини виразів (3) та (4), отримаємо . Але для оболонки, яка не має опору у осьовому напрямку, осьове напруження відсутнє, тобто . Підставляючи в отримане рівняння значення напруження _t з (2), маємо:

; . (5)

3. Обґрунтування розрахункових залежностей до визначення напружень та деформацій за моментною теорією оболонок

Як показано в навчальному посібнику [2], за моментною теорією напружений стан оболонки описується диференційним рівнянням поздовжньо – поперечного згину.

(6)

де – циліндрична жорсткість, Нм²; – параметр, м^-1. Для циліндричної оболонки сталої товщини:

(7)

Розв’язання диференційного рівняння має вигляд [2]:

, (8)

де 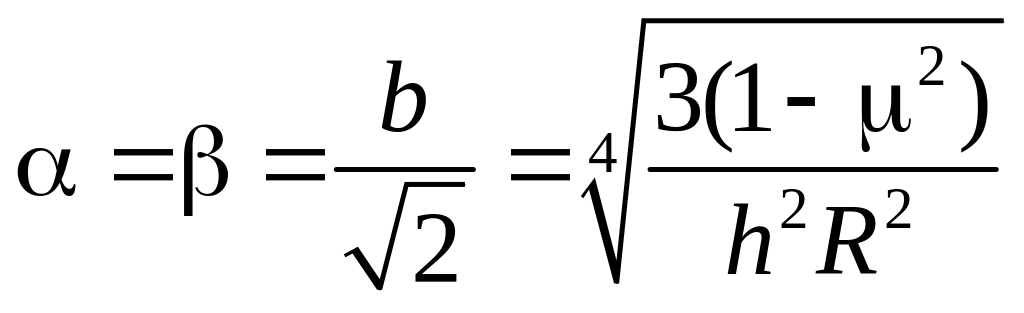; – частинне рішення рівняння (6), обумовлене видом правої частини.

Частинне рішення за виглядом правої частини диференційного рівняння (6) приводиться до наступного вигляду

. (9)

Для довгих оболонок впливом закріплень одна до одної можна нехтувати. У такому випадку рішення (8) скорочується і з урахуванням (9) має вигляд

(10)

Визначення вільних сталих і відбувається за допомогою граничних умов, якими є умови закріплення оболонки ротора у його цапфах при : . Для спрощення перетворень введемо безрозмірні величини, аргумент і функцію . Використовуючи їх та умови закріплення, знаходимо: ; .

Таким чином, рішення (10) набуває наступного вигляду

. (11)

Згинаючий момент можна визначити за допомогою другої похідної функції прогину (10), тобто . З урахуванням (11) і відповідних перетворень ця залежність приводиться до наступної форми

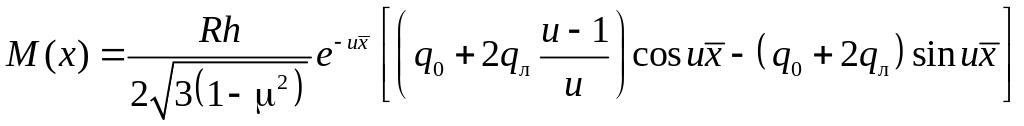. (12)

Визначимо згинаючий момент у місті закріплення оболонки ротора, тобто при . З наведеного рішення (12) знайдемо наступне значення

. (13)

З урахуванням (13) спростимо розрахункову залежність (12)

, (14)

де 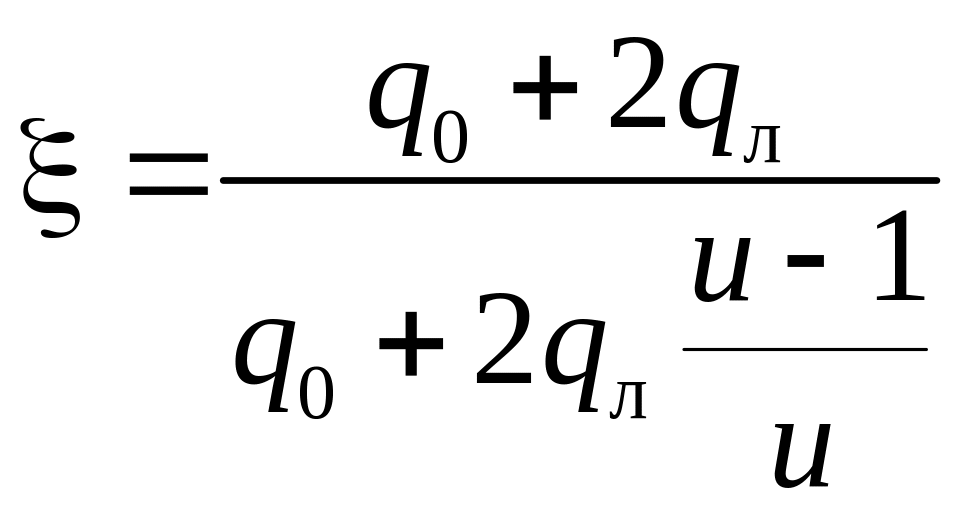, – відносна координата.

Враховуючи те, що згинаючий момент є розподіленим навантаженням, можна знайти максимальні напруження у поперечному перерізі (на поверхнях оболонки) від згинаючого моменту:

(15)

Максимальне значення напруження виникає у торцевому перерізі, коли згинаючий момент : .

В напрямку осі y нормальне напруження визначається за залежністю Пуасона:

. (16)

З врахуванням (15) та (16) величини нормальних напружень визначаються за формулами:

, (17)

. (18)