Задание
Продолжите фразу: Числовая окружность – это…
Отметим на числовой окружности характерные точки – этим точкам соответствуют точки пересечения с осями координат: 0 (начало отсчета); 2 (длина всей окружности); (длина половины окружности); /2; 3/2; –/2.
3,14, значит, за указанными характерными точками стоят действительные числа числовой окружности: 0; 3,14; 6,28; 1,57; 4,71; –1,57.
Вернемся к основной проблеме (стр. _____): что является _____________________ _____________ _________________________________________?
________________________________________________________________ является _____________________________________________________________________________.
Чтобы не ошибаться при работе, например, с выражением sin 2, рекомендуется: к аргументу тригонометрической функции добавить наименование «радиан» и представить себе угол поворота на заданное число радиан. В данном случае: дан синус двух _______;
а это угол, примерно равный ____________ градусов.
5. Определение синуса и косинуса; тангенса и котангенса на единичной окружности.
Определения. Рассмотрим окружность единичного радиуса с центром в начале координат. Пусть точка на окружности, начав движение в точке М0 (1, 0), прошла по окружности дугу величиной х радиан, или же соответствующий этой точке луч (отрезок, вектор) повернулся на угол х радиан. Пусть Мх – положение точки на окружности в конце движения. Эта точка полностью описывается ее координатами, поэтому для них вводят специальные обозначения.
Ординату точки Мх (или проекцию точки на ось ординат) называют синусом числа х, а абсциссу (или проекцию на ось абсцисс)– косинусом числа х.
Элемент математической культуры как компетенция
ЭМК Работа с определением
Основная цель работы с определением – выделить существенные признаки определяемого понятия.
Задание
Ответьте на вопрос: «Какие условия надо раскрыть, определяя синус (косинус)?» (выделенные условия последовательно отразите на рисунке).
Определения. Тангенсом числа х называется отношение синуса данного числа к его косинусу. Котангенсом числа х называется отношение косинуса данного числа к его синусу.
;
.
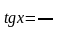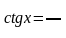Задание
Найдите значения синуса, косинуса, тангенса и котангенса для углов 0; 2; ; /2; 3/2. и результаты отразите в таблице.
Значения тригонометрических функций в характерных точках окружности
Число функция |
0 |
2 |
|
/2 |
3/2 |
Синус |
|
|
|
|
|
Косинус |
|
|
|
|
|
Тангенс |
|
|
|
|
|
Котангенс |
|
|
|
|
|
Организация записей как компетенция
Систематизируйте информацию в виде таблицы. Заголовок таблицы должен отражать название системы, название 1-ой строки и 1-го столбца – ее основные характеристики.