Теорема Стокса та формула Гріна

• Теорема Стокса. Якщо в деякій області, яка містить гладку поверхню S та її межу L, проекції вектор-функції та їх частинні похідні першого порядку є неперервними функціями, тоді має місце рівність:

(17)

Смисл рівності (17) в тому, що при виконанні умов теореми циркуляція поля вздовж замкненої лінії L, яка обмежує поверхню S, дорівнює потоку поля rot через поверхню S.

Розглянемо частинний випадок теореми Стокса.

Нехай контур L обмежує плоску область D і система координат вибрана так, що D лежить в площині xOy.

Тоді оскільки нормаль до довільної точки області D співпадає з напрямком осі Oz.

Маємо:

Підставимо ці вирази в рівність (17) і отримаємо:

(18)

Якщо ввести позначення

і розглядати Р(x, y) та Q(x, y) як довільні функції (вектор-функція розглядалась з довільними проекціями), то (18) прийме вигляд

(19)

Ця формула називається формулою Гріна. Вона описує зв’язок між подвійним інтегралом по плоскій області D з криволінійним інтегралом по межі L цієї області.

• Приклад. Знайти потік вихору поля 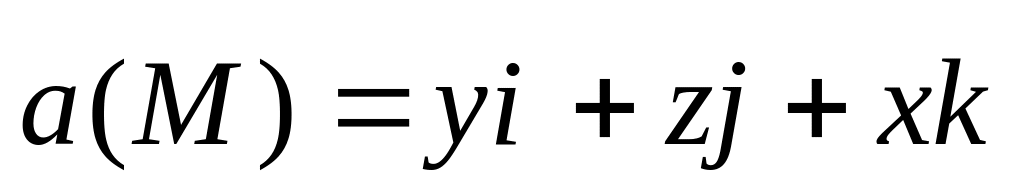через поверхню обертання 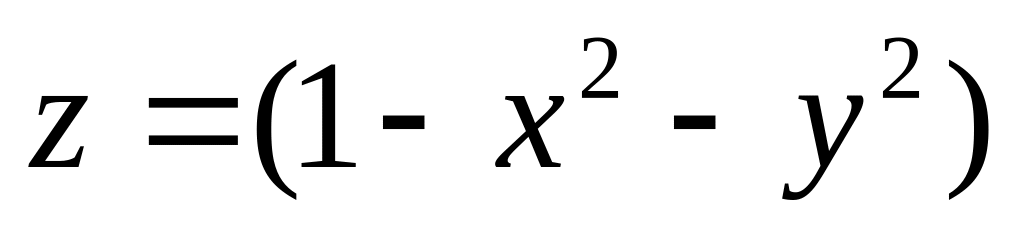обмежену площиною z = 0.

Розв’язання. Позначимо задану поверхню обертання – параболоїд через S. В перетині поверхні S та площини z = 0 знаходиться замкнена лінія L: x² + y² = 2, яка є межею поверхні S.

Потік П поля rot через поверхню S шукаємо за формулою:

Застосовуючи формулу Стокса (17), отримаємо

В даному випадку лінія L плоска, тому

оскільки z = 0 на L.

Отже, одержали, що

, де L – коло

В параметричному запису лінія L:

.

Перейдемо від криволінійного інтеграла до визначеного:

4. Оператори Гамільтона та Лапласа. Диференціальні операції другого порядку теорії поля

3.4.1 Оператор Гамільтона та правила його користування

• Означення 4. Оператором Гамільтона називають символічний векторно-диференціальний оператор, який позначають знаком (набла) і визначають в декартовій системі координат рівністю

(20)

де , , - орти координатних осей.

Підкреслимо, що оператор є символічним вектором, тому він не може бути рівним, паралельним або перпендикулярним реальному вектору .

Оператор часто використовується і навички його застосування полегшують вивчення багатьох дисциплін, особливо електротехніки.

Основні правила користування оператора

1. Оператор діє на величини, які стоять за ним, і не діє на величини, які стоять перед ним.

Так, в запису оператор діє на і не діє на . Іноді, щоб вказати величину, на яку не діє оператор , у цій величині ставиться індекс, що вказує на необхідність розглядати цю величину як сталу. Наприклад, в запису слід розуміти, що на не діє, а на діє.

2. Добуток оператора на суму двох функцій обчислюють за формулою:

3. Скалярний добуток оператора на суму двох векторів обчислюють за формулою:

4. Векторний добуток оператора на суму двох векторів обчислюють за формулою:

5. Добуток оператора на скалярну функцію дорівнює градієнту фунуції , оскільки

Англійський математик Гамільтон помітив, що через скалярний та векторний добутки векторів та можна виразити характеристики векторного поля та

Дійсно,

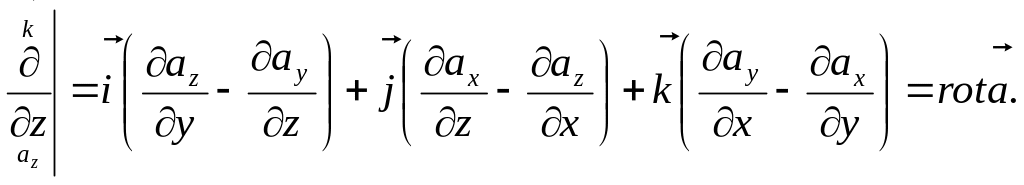
Маємо:

Отже,

1. для знаходження градієнта скалярного поля u=u(x, y, z) потрібно оператор помножити на функцію u;

2. для знаходження дивергенції вектора потрібно оператор скалярно помножити на вектор ;

3. для знаходження вихору вектора потрібно оператор векторно помножити на вектор .

• Означення 5. Процес знаходження характеристик grad u, div , rot називають операціями першого порядку теорії поля.

Зауваження. Для пояснення техніки використання оператора згадаємо правило диференціювання добутку двох функцій

(21)

Перший доданок правої частини отримується, якщо диференціювати добуток , вважаючи сталою, а другий доданок – якщо при диференціюванні добутку вважати множник сталим.

Тому формулу (21) можна розуміти так:

Коли диференціювання закінчено індекс с у відповідних величин можна зняти.

Аналогічним чином доцільно поступати при обчисленні результату дії оператора “набла” на добуток двох функцій або функції та вектора або добутку двох векторів.

• Приклад.

• Приклад.

• Приклад.

Враховуючи властивість векторного добутку

одержуємо:

• Приклад.

Доданки правої частини цієї рівності є мішаними добутками трьох векторів , та . Якщо в мішаному добутку поміняти місцями два поряд записаних множника, то добуток змінює знак. Тому

Отже,