18

Державний університет телекомунікацій

Навчально-науковий виробничий центр, м. Львів

Затверджую

Зав. ННВЦ

__________ Яковлєва Т.С.

“___” _______ 2014 р.

Опорний конспект лекцій

з дисципліни “Вища математика”

для студентів заочної, прискореної форми навчання

(ІІІ курс, V семестр), лекція 2

Теорія скалярних та векторних полів

Склав: доцент, к.ф.-м.н.

Плешівський Я.М.

м.Львів-2014 р.

Розділ 3. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ

3.1 Визначення полів та їх характеристики

Теорія поля є важливим і перспективним розділом вищої математики, оскільки на кожну людину впливає космічне поле, поле тяжіння Землі, електричні та магнітні поля, біополя.

• Означення 1. Фізичним полем називають частину простору або весь простір, в якому здійснюється фізичне явище.

Якщо деяка фізична величина в кожній точці області приймає певне значення, то тим самим задається поле цієї величини.

• Означення 2. Якщо фізична величина в кожній точці області приймає певне числове значення, то поле називають скалярним.

Скалярне поле величини u в області D можна задати у вигляді скалярної функції

u = u(M), M  D,

областю визначення якої є D.

• Означення 3. Якщо фізична величина в кожній точці приймає векторне значення, то її поле називається векторним.

Векторне поле в області D задається вектор-функцією

, M  D.

Якщо D  Е₃, то положення точки M  D визначається координатами x, y, z. Тому скалярне поле задається скалярною функцією трьох змінних

u = u(x, y, z).

Векторне поле в тривимірному просторі визначається

,

тобто трьома скалярними функціями-проекціями на відповідні осі координат.

Векторне поле називають плоским, якщо його можна задати у вигляді

.

3.1.1 Основні характеристики скалярного поля

1. Поверхні (лінії) рівня визначають точки в яких функція приймає однакове значення. Поверхні рівня скалярного поля u = u(x, y, z) визначають рівнянням

u(x, y, z) = c. (1)

Лінії рівня поля u = u(x, y) визначають рівнянням

с = u(x, y). (1^’)

2. Похідна за напрямом характеризує швидкість зміни поля в напрямку вектора , її знаходять за формулою

, (2)

де - напрямні косинуси .

3. Градієнт скалярного поля u = u(x, y, z) визначає напрям та величину найбільшої зміни поля в точці M(x, y, z). градієнт знаходять за формулою

gradu(M) = (3)

а величина найбільшої швидкості зміни поля знаходиться за формулою

Напрям вектора gradu співпадає з напрямом нормалі до поверхні u(x, y, z) = c в точці М, оскільки

grad u = . (4)

• Приклад 1. Визначити поверхні рівня, похідну за напрямком та градієнт поля u = x² + (y + 1)² + (z – 2)² в точці М₀ (1, 1, 1).

Розв’язання. Рівнянням поверхонь рівня заданого поля буде

x² + (y + 1)² + (z – 2)² = с,

тобто поверхнями рівня заданого поля будуть сфери з центром в точці А(0; -1; 2) радіусом . Підставимо замість x, y, z координати точки М₀, тоді одержимо

1+ (1 + 1)² + (1 – 2)² = с с = 6.

Отже, через точку М₀ проходить одна поверхня рівня, рівняння якої буде

x² + (y + 1)² + (z – 2)² = 6.

Знайдемо частинні похідні функції u в точці М₀:

За формулою (2) одержимо:

Оскільки

то

За формулою (3) знаходимо градієнт поля в точці М₀:

3.1.2 Характеристики векторного поля

1. Векторною лінією поля 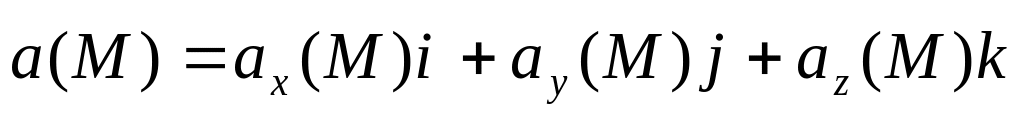називають лінію, в кожній точці якої дотична співпадає з напрямом .

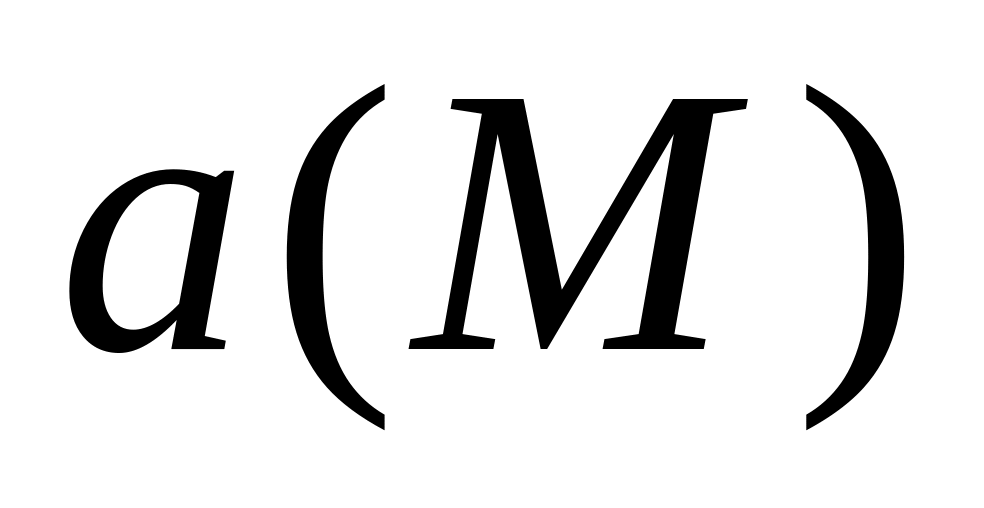Якщо координати векторного поля неперервні разом із своїми похідними першого порядку в точці М₀, то через точку М₀ проходить лише одна векторна лінія.

Рівняннями векторних ліній будуть розв’язки диференціальних рівнянь

. (5)

2. Особливі точки векторного поля. Точку М₀ називають особливою точкою поля , якщо або хоч би одна з проекцій цього поля має розрив в точці М₀.

Найчастіше фізичні векторні поля мають неперервні проекції, а їх особливими точками є точки, де і які називають точками спокою.

Точки спокою класифікують в залежності від виду векторних ліній в околі цих точок.

3. Потік векторного поля через поверхню S характеризує різницю П = N₊ - N_-, де N₊ - кількість векторних ліній поля, які проходять через поверхню S і мають однаковий напрям з нормаллю до цієї поверхні, а N_- - кількість векторних ліній поля, які мають протилежний напрям.

Потік векторного поля через поверхню S визначають поверхневим інтегралом другого роду за формулою:

П = (6)

де - нормаль до поверхні S в точці М.

4. Дивергенція (розходження) векторного поля характеризує щільність потоку поля через замкнену поверхню S в точці М, яка знаходиться в області, що обмежена S.

Дивергенцію векторного поля обчислюють за формулою:

(7)

Точки М, в яких 0, називають джерелами векторного поля. Точки М, в яких 0, називають точками стоку (стікання).

5. Роботу Р змінної сили при переміщенні точки визначають криволінійним інтегралом другого роду за формулою:

(8)

6. Циркуляція С векторного поля характеризує обертальну спроможність поля і її знаходять з використанням криволінійного інтеграла другого роду за формулою:

(9)

де L – деякий замкнений контур, - диференціал радіуса-вектора точки М  L.

7. Вихор векторного поля є вектором, який характеризує поверхневу щільність циркуляції, позначають 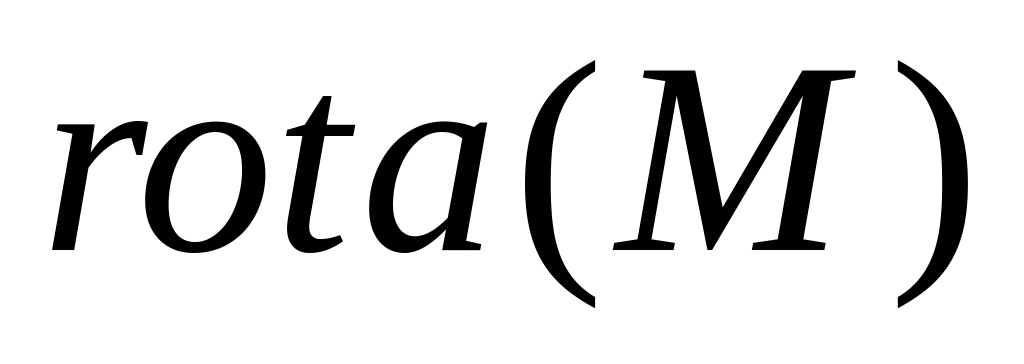, визначають формулою:

Останню формулу можна записати у більш прийнятому для використання вигляді:

. (10)

Добуток символів частинних похідних та координат вектора треба розуміти як відповідні частинні похідні першого порядку відповідних функцій. Наприклад:

• Приклад 2. Знайти векторні лінії, дивергенцію та вихор поля

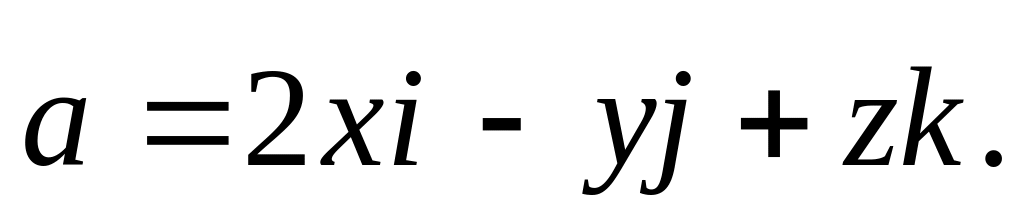
Розв’язання. Для знаходження рівнянь, векторних ліній заданого поля треба знайти розв’язки системи диференціальних рівнянь (5), які приймають вид:

1) 2)

Інтергуючи рівняння першого порядку з відокремленими змінними отримаємо сукупність ліній:

1)

2)

Відмітимо, що початок координат є особливою точкою для заданого поля, оскільки при і маємо .

Дивергенцію поля знайдемо за формулою (7):

Вихор векторного поля знайдемо за формулою (10):

= .
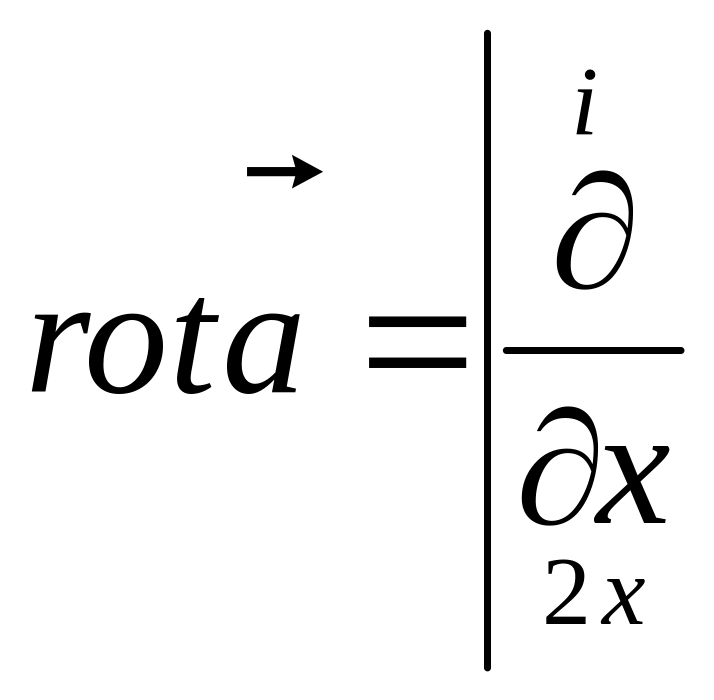