9 Самостійна робота 8

Тема: Визначення кінематичних параметрів тіла із застосуванням основного рівняння руху та закону зміни кінетичної енергії

Питання, що розглядаються

1 Основні теореми динаміки

2 Кінетична енергія при різних видах руху тіла

3 Основне рівняння обертового руху тіла

4 Розв’язання задач

Для розв’язання задач динаміки часто необхідно застосовувати теорема про зміну кількості руху (імпульсу) матеріальної точки, закон про зміну кінетичної енергії та основне рівняння обертового руху тіла.

Теорема про зміну кількості руху (імпульсу) матеріальної точки

mV₁- mV₂=

тобто геометричний приріст кількості руху (імпульсу) рухомої ма­теріальної точки за скінчений проміжок часу дорівнює імпульсу при­кладеної сили за той самий проміжок часу. Приріст кінетичної енергії матеріальної точки на скінченній ділянці шляху дорівнює роботі рівнодіючої всіх сил, прикладених до точки, на тій самій ділянці шляху.

Слід навчитися визначати кінетичну енергію тіла під час різних видів руху.

Потенціальна енергія сили тяжіння - це здатність тіла виконувати роботу при опусканні з деякої висоти до рівня моря:

П=GH

Для матеріальної точки кінетична енергія чисельно дорівнює напівдобутку

маси на квадрат швидкості:

Е=

Кінетична енергія також вимірюється в одиницях роботи.

При поступальному русі тіла швидкості всіх його точок рівні між собою і мають однакові направлення. Кінетична енергія тіла

Е=

где М — масса всего твердого тела, Vс-швидкість центру мас тіла.

Кінетична енергія тіла при плоско паралельному русі складається з кінетичної енергії поступа­льного руху разом з полюсом і кінетичної енергії обертального руху навколо полюса.

Е=

При вирішенні задач динаміки виникає необхідність застосування основного рівняння обертового руху твердого тіла-роторів, валів, маховиків та інших. Це рівняння має вигляд:

- добуток моменту інерції тіла на кутове прискорення дорівнює сумі моментів всіх сил відносно осі обертання.

Задачі до розв’язання.

Задача 1. Під час пуску електродвигуна його ротор діаметром D обертається під дією постійного моменту М₁. У підшипниках електродвигуна виникає момент сил тертя М₂. Вважаючи ротор однорідним циліндром масою m визначити кількість обертів ротора та кутову швидкість за час t після початку руху.

Задача 2. Поїзд масою m=3∙10⁶кг рухається по прямій зі швидкістю V та почав гальмування. Гальмівний шлях склав L. Визначити гальмівну силу та час гальмування.

Задача 3. Однорідний диск діаметром D и масою m з катиться по поверхні зі швидкістю V. Визначити кінетичну енергію диска.

Таблиця 1- Вихідні дані задач 1-3

варіант	m, кг	М1,Нм	М2,Нм	D, м	T,с	V,м/с	L,м
1	10	80	8	0,2	5	15	300
2	30	82	8	0,25	6	18	400
3	12	85	9	0,3	7	19	350
4	28	90	9	0,35	8	20	450
5	15	94	9	0,4	9	21	600
6	25	96	10	0,45	10	25	600
7	17	100	10	0,5	14	24	700
8	22	115	11	0,55	12	23	800
9	18	106	9	0,6	11	22	900
10	20	90	9	0,65	9	28	550

Задача 4. Маховик (суцільний диск) діаметром D і масою m обертається по інерції з постійною кутовою швидкістю n за вказаним напрямом (рисунок 1). Зупинка маховика здійснюється натисканням гальмівної колодки за допомогою важіля aob. Яку силу необхідно докласти до точки b важіля, щоб зупинити маховик за t(с). Обертання маховика під час гальмування вважати рівносповільненим. Скільки обертів зробить маховик до зупинки від початку гальмування? Коефіцієнт тертя колодки і маховика f=0,4.

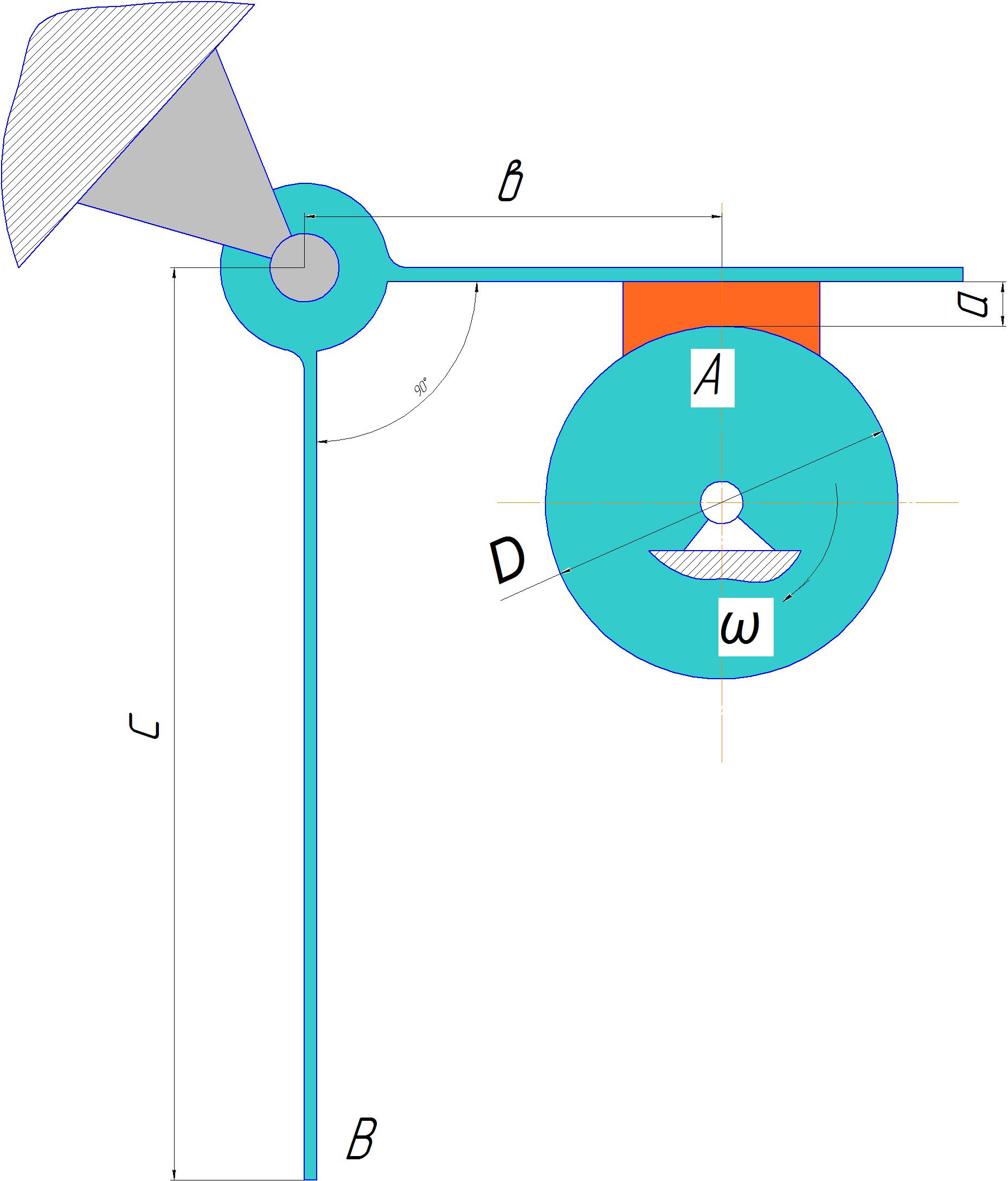
Рисунок 1- Схема колодкового гальма

Таблиця 2- Вихідні дані задачі 4

Варіант	m, кг	n, об/хв	D, мм	c, мм	b, мм	a, мм	t, с
1	10	950	200	130	50	80	40
2	12	1200	250	150	65	70	30
3	15	1100	300	120	40	60	20
4	17	1450	350	150	60	90	25
5	20	2500	400	120	50	75	35
6	22	800	450	135	45	65	45
7	30	900	500	140	40	85	50
8	35	1200	550	150	60	95	55
9	24	1300	400	160	65	100	60
10	14	1400	300	200	70	105	65

Питання для самоконтролю

1. Що називається кількістю руху матеріальної точки?

2. Що називається елементарним імпульсом сили?

3. Який вид має рівняння, що виражає тео­рему про зміну кількості руху матеріальної точки?

4. Який вид має рівняння, що виражає теорему про зміну кількост руху за кінцевий проміжок часу і як в цьому випадку формулюється теорема?

5. Який вид мають рівняння, що виражають теорему про зміну кількості руху матеріальної точки за кінцевий проміжок часу в проекціях на осі декартової системи координат?

6 Який вид має формула, яка виражає в диференціальній формі теорему про зміну кінетичної енергії, і як в такому випадку формулюється теорема?