8 Самостійна робота 7

Тема: Розрахунки механізмів з врахуванням тертя

Питання, що розглядаються

1 Тертя ковзання, конус тертя

2 Тертя кочення

3 Робота сили, коефіцієнт корисної дії

4 Розв’язання задач

Сила тертя ковзання Fт пропорційна нормальному тиску N, прикладена на поверхні стику деталей і направлена у бік, протилежний швидкості

F_т=f∙N

f - безрозмірний коефіцієнт тертя ковзання, що визначається експериментально (для сталевих деталей без мастила f=0,12...0,15, а для змащених сталевих деталей f=0,05...0,08).

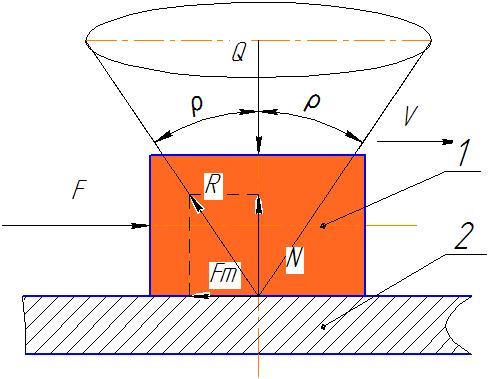
Рисунок 1- До визначення тертя ковзання.

За наявності сили тертя сумарна реакція є гео­метричною сумою нормальній складовій та сили тертя

R=N+F_т

та відхиляється від нормалі на деякий кут ρ, який носить назву кута тертя:

tgρ=

Якщо навколо вісі, перпендикулярної опорній площині, шляхом обертання вектора повної реакції утворити поверхню кру­гового конусу, то отримуємо так званий конус тертя з кутом при вершині, що дорівнює подвійному куту тертя. Коли лінія дії рівнодіючій всіх сил, прикладених до тілу, розташована в середині конуса тертя, то, як би не була ця сила, вона не зможе вивести тіло з стану рівноваги. Це явище носить назву самогальмування і широко використовується в механізмах. Так, тіло, на похилій площині, буде ковзати по ній при куті нахилу, більшому, ніж кут тертя. Якщо ж кут нахилу площини менше кута тертя, тіло залишиться у спокої внаслідок самогальмування. Важливе значення має розрахунок сил, роботи сил та к.к.д. похилої площини. Схема сил, діючих на тіло на похилої площині наведена на рисунку.

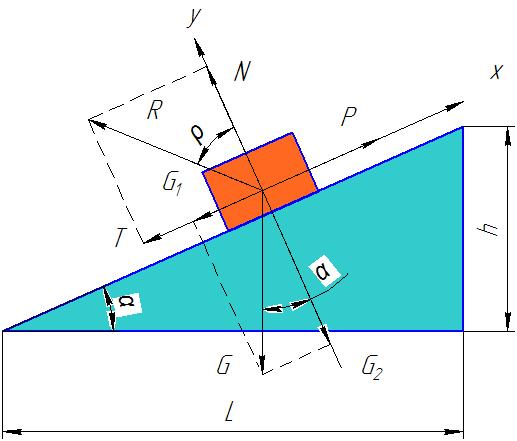
Р- рушійна сила;

G- сила ваги вантажу;

G₁, G₂-проекції сили ваги вантажу відповідно на вісі х та у;

- сила нормальної реакції з боку похилої площини;

сила тертя;

R- рівнодіюча сил N та T.

Коефіцієнт корисної дії похилої площини в випадку, коли рушійна сила F паралельна площині

Сила тертя кочення визначається за формулою:

F_тк =Nk/r,

де k - коефіцієнт тертя кочення, мм,

г- радіус ролика, мм.

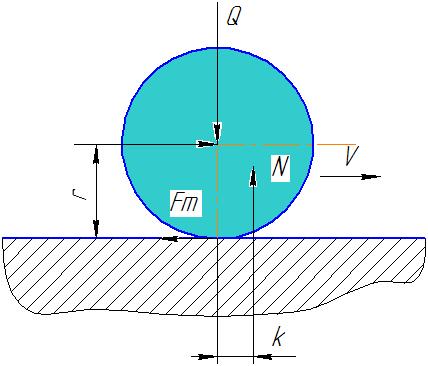
Рис. 1. Схема до визначення сил тертя кочення

Коефіцієнт тертя кочення к знаходять дослідним шляхом: для пари деталей із незагартованих сталей к = (0,004...0,005) мм, а для пари деталей із загартованих сталей к = (0,001...0,002) мм.

Тертя призводить до втрат потужності, тому корисна робота Ак завжди менше витраченої А_в, і їх відношення визначає коефіцієнт корисної дії, який завжди менше одиниці.

Робота постійної за величиною сили F

А=FSсоsα

де S-переміщення,

α-кут між напрямком лінії дії сили та переміщенням.

Задача 1. Вантаж масою m за допомогою похилої площини з кутом підйому α піднятий на висоту h силою, паралельною похилій площині із постійною швидкістю. Визначити роботу сили, коефіцієнт тертя f.

варіант	m, кг	αº	h, м	f	D, м	W, Дж.	f, мм	L, м
1	100	15	1	0,05	0,2	2000	0,003	3
2	300	30	2	0,06	0,25	2500	0,004	4
3	120	18	1,2	0,07	0,3	2600	0,0035	3,5
4	280	32	1,8	0,08	0,35	2700	0,0045	4,5
5	150	20	1,3	0,08	0,4	2800	0,005	6
6	250	28	1,7	0,1	0,45	2900	0,0035	6
7	170	25	1,4	0,11	0,5	3000	0,003	7
8	220	35	1,6	0,12	0,55	3500	0,0045	8
9	180	17	1,5	0,13	0,6	3800	0,005	9
10	200	12	2,5	0,15	0,65	4000	0,004	10

Задача 2. По похилій площині з кутом підйому α вкочують каток масою m і діаметром D. Сила тяги паралельна похилій площині. Визначити висоту, на яку буде піднятий каток, якщо затрачена робота тяги W, коефіцієнт тертя кочення f(мм).

Задача 3. Тіло масою m рівномірно переміщується вверх по похилій площині довжиною L з кутом підйому α. Визначити величину роботи рушійної сили, яка спрямована паралельно похилій площині та к.к.д похилої площини. Коефіцієнт тертя f.

Задача 4. Визначити роботу, яку необхідно виконати для перекочування катка масою m на відстань L по горизонтальній не гладкий поверхні силою, яка прикладена до осі катка та спрямована горизонтально. коефіцієнт тертя кочення f(мм.)

Для всіх задач необхідні данні взяти з таблиці. Для задачі 4 для всіх варіантів прийняти

Питання для самоконтролю.

1 Пояснить природу сил тертя.

2 Як знайти роботу постійної сили на кінцевому переміщенні?

3 Як побудувати конус тертя?

4 Пояснити явище самогальмування.