7 Самостійна робота 6

Тема: Визначення швидкостей і прискорень точок твердого тіла в складному русі

Питання, що розглядаються

1. Швидкість і прискорення точки твердого тіла в складному русі

2. Роз’вязання задачі.

В багатьох випадках є необхідність розглядати рух точки або тіла відносно рухомої системи координат. Наприклад, по вагону потягу йде людина. При цьому рух потягу буде переносним, а рух по відношенню до вагону - відносним.

Рух точки по відношенню до рухомої системи координат будемо називати відносним. Під переносним рухом розуміють рух нерухомої системи координат відносно нерухомої.

Встановлення зв’язку між складним, відносним і переносним рухами дозволить розв’язувати задачі по визначенню кіне­матичних характеристик руху точок твердого тіла.

Введемо такі значення:

V_А, а_А - абсолютні швидкість та при­скорення;

V_е, а_е - відносні швидкість та прискорення;

V_r , а_r - перено­сні швидкість та прискорення (швидкість та прискорення тієї точки ру­хомої системи координат,

Абсолютна швидкість точки визначається як геометрична сума відносної та переносної швидкості:

, (1)

Абсолютне прискорення знаходиться в залежності від характеру переносного руху. Якщо переносний рух є поступальним, то абсолютне прискорення точки визначається як геометрична сума відносного та переносного прискорення:

Якщо переносний рух є обертовим з кутовою швидкістю , то абсолютне прискорення точки визначається як геометрична сума відносного переносного прискорення та прискорення Коріоліса:

Величина Коріолисова прискорення:

Напрямок прискорення Коріолиса знайти за правилом М. Є. Жуковського: повернути вектор відносної швидкості за напрямком обертання переносного руху.

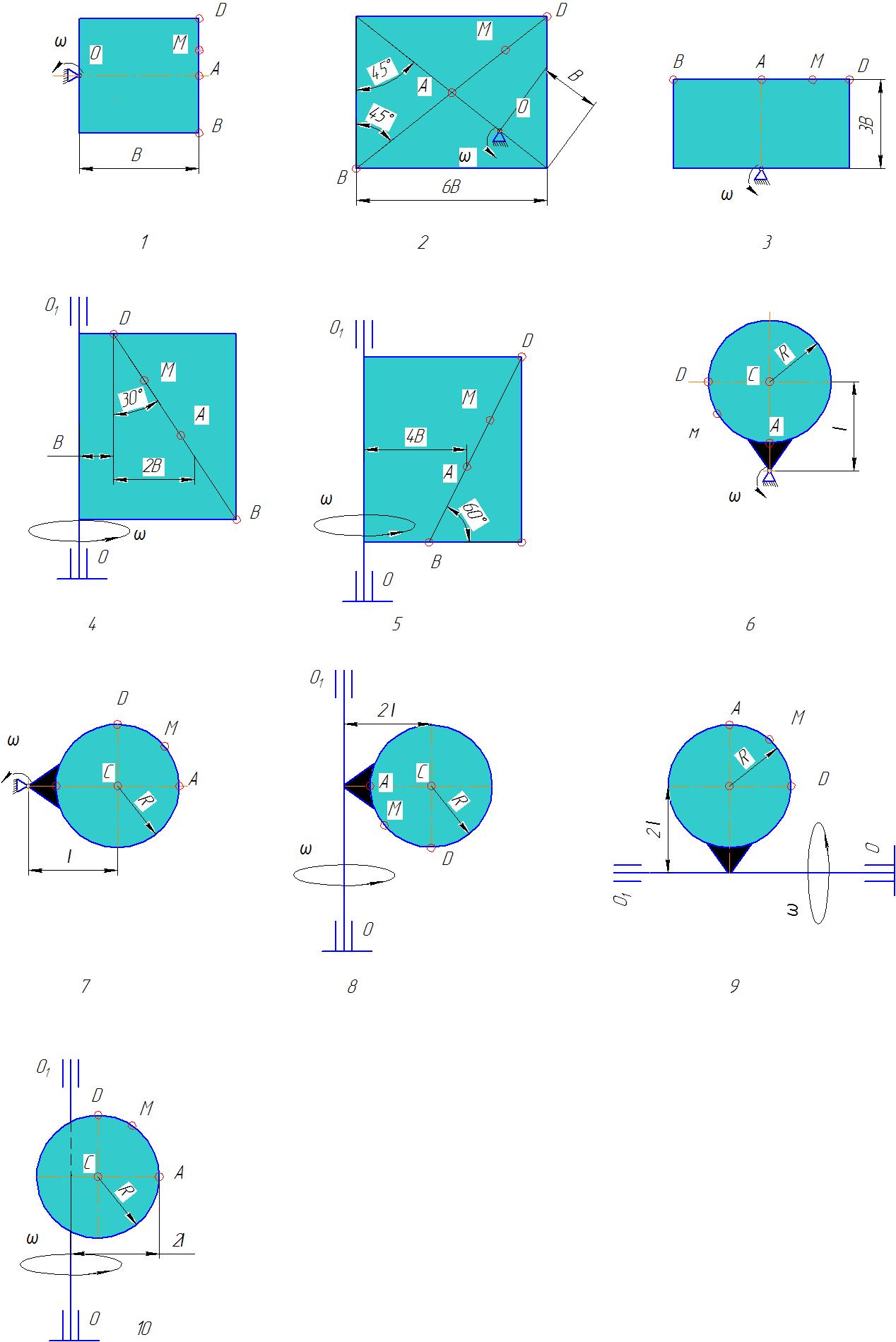
Задача. Прямокутна або кругла пластина радіусу R = 60см обертається навколо нерухомої осі за законом φ=f₁(t), що заданий у таблиці 1. Додатній напрямок відліку кута φ показано на рисунках дуговою стрілкою. По пластині вздовж прямої ВО або вздовж кола радіусу R рухається точка М. Закон її відносного руху s=f₂(t), (s виражено у сантиметрах, t-в секундах), заданий у таблиці 1. На рисунках точка М показана у положенні, при якому s=АМ>0 (при s<0 точка М знаходиться з іншого боку від точки А).

Знайти абсолютну швидкість та абсолютне прискорення точки М у момент часу t=1с.

Приклад. Дано Визначити абсолютну швидкість та абсолютне прискорення точки В₁ в даний момент часу.

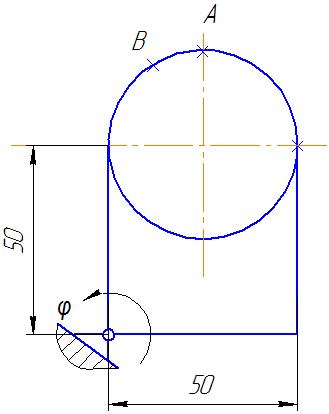
Рисунок 1- схема пластини

Розглянемо рух точки В як складний, який складається з відносного руху по дузі кола та переносного руху у вигляді обертання пластини навколо точки О.

Визначаємо положення точки В у заданий час t=2с:

, тоді кутове положення точки В:

<

Знак «мінус» беремо з врахуванням, що точка В лежить на дузі по інший бік від точки А, ніж точка В. Визначаємо значення відносної швидкості:

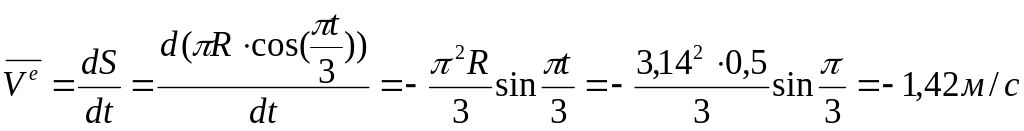
Знайти кутову швидкість переносного руху:

Визначаємо значення переносної швидкості:

Модуль абсолютної швидкості можна знаходити, знайшовши попередньо значення проекцій і та і та визначити

(1)

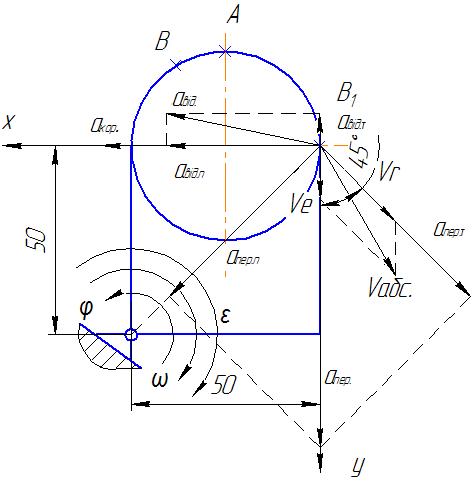
Рисунок 2- швидкості та прискорення точки В₁

Якщо можна визначити кут між векторами та ( в даному випадку ) то

Абсолютне прискорення точки В у складному русі:

(2)

Оскільки і відносний і переносний рух є обертовим, то прискорення можна розкласти на нормальні та дотичні складові:

та , тоді рівняння (2) прийме вигляд:

(3)

Знаходимо дотичне відносне прискорення:

Нормальне відносне прискорення:

Знаходимо дотичне переносне прискорення:

де - кутове прискорення пластинки у переносному русі:

Тоді

Нормальне переносне прискорення:

Визначаємо величину Коріолісова прискорення.

а_кор=2ωV_r=

Напрямок а_кор знаходимо за правилом М. Є. Жуковського, обернувши вектор V_r за напрямком ω.

Тепер, коли відомі всі складові абсолютного прискорення, його модуль можна знайти двома способами:

• знайти проекції складових абсолютного прискорення на осі та розраховувати його модуль ;

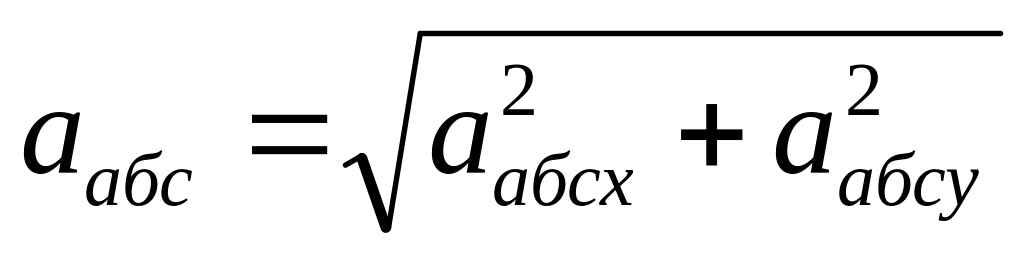• побудувати векторний план прискорень в обраному масштабі та визначити з плану .

Обираємо осі координат з центром у точці В.

Проектуємо рівняння (3) на осі Вх і Ву:

Знаходимо абсолютне прискорення точки В методом побудови плану прискорень в масштабі . З плану прискорень знаходимо

, що співпадає з методом проекцій.

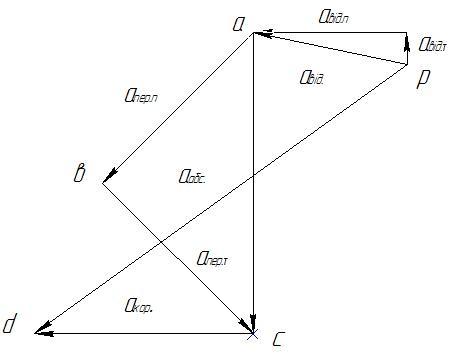
Рисунок 3-план прискорень точки В₁.

Таблиця 1-Вихідні дані

Варіант, № схеми	Переносний рух	Відносний рух	Розміри, см
	φ=f1(t)	s=АМ=f2(t)	l	В, см
1	4(t2-t)	50(3t-t2)-64	-	12
2	3t2-8t	40(3t-t2)-32	-	8
3	6t3-10t2	80(t2-t)+40	-	9
4	t3-2t2	50(t-2t2)-40	-	20
5	10t2-5t3	π/3R(4t2-2t3)	R	-
6	5t-4t2	π/2R (2t3-t2)	4/3 R	-
7	2t3-10t	π/3R(t3-2t)	R	-
8	6t2-3t3	π/6R(t3-2t2)	3/4 R	-
9	2(t2-t)	π/2R(t-2t2)	R	-
10	5(t2-t)	π/3R(t2-1)	1,3 R	-

Питання для самоконтролю.

1. Що називається складним рухом точки (тіла)?

2. Коли виникає прискорення Коріоліса?

3. Запишіть загальні формули визначення абсолютної швидкості і абсолютного прискорення.