5 Самостійна робота 4

Тема: Визначення кінематичних параметрів точки при поступальному та обертовому русі

Питання, що розглядаються

1. Координатний спосіб завдання руху.

2. Визначення геометричних параметрів руху.

3. Розв’язання задачі.

До самостійної роботи слід приступати після вивчення теми «Кінематика точки», з'ясувавши поняття про кінематичні параметри руху точки –шлях, траєкторію, швидкість, нормальне, дотичне та повне прискорення.

При русі у площині рівняння руху точки при координатному способі завдання руху:

(1)

Для отримання рівняння траєкторії з рівнянь (1) необхідно виключити параметр часу t. Для розрахунку швидкості точки необхідно знайти проекції швидкості на вісі координат:

, , (2)

Модуль швидкості

(3)

Аналогічно прискорення точки:

, , (4)

Дотичне прискорення розраховують за формулою

, (5)

а нормальне прискорення слід шукати з залежності

(6)

Радіус кривизни траєкторії в заданій точці:

(7)

Приклад. Рух точки М задано рівняннями ( х та у задано у см, t в сек.)

Визначити траєкторію точки, закон іі руху, швидкість, прискорення та радіус кривизни траєкторії в момент часу t=2c.

Розв’язок. Для визначення траєкторії виключаємо з рівнянь (1) час t.

Застосовуємо формулу

sіn²α +соs²α=1

та отримаємо

Таким чином, траєкторія точки є коло радіусом r=5см. Будуємо траєкторію точки в декартової системі координат та знаходимо положення точки в момент часу t=2c

Визначаємо проекції швидкості:

Модуль швидкості

Знаходимо шлях точки

, або

При часі t=2c

Знаходимо прискорення точки:

Повне прискорення:

Дотичне прискорення:

Нормальне прискорення точки М:

Радіус кривизни траєкторії в заданій точці:

З точки М проводимо знайдені вектори у обраному масштабі. Швидкості та прискорення точки М наведено на рисунку 1.

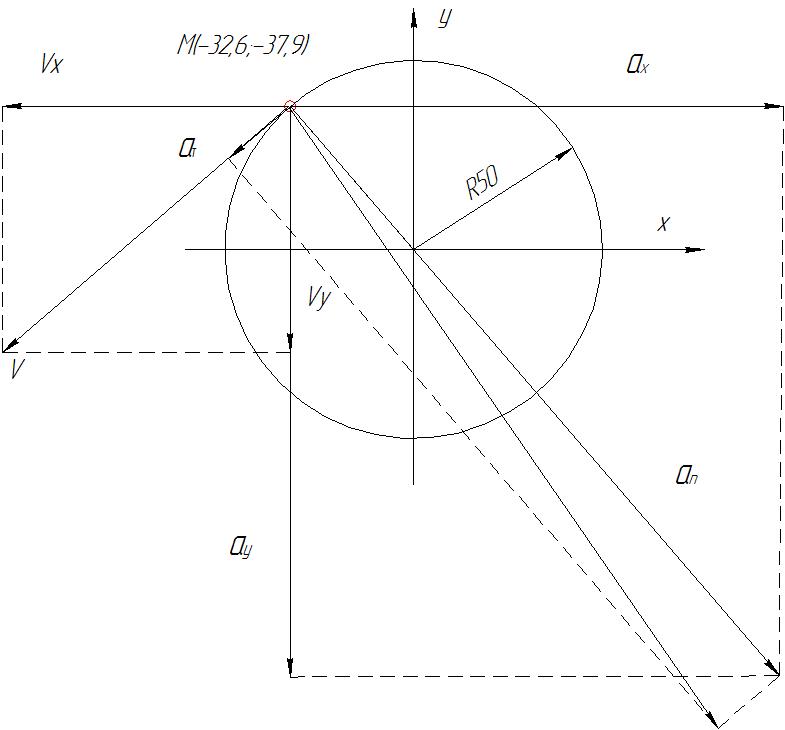
Рисунок 1- Траєкторія, швидкість, прискорення та радіус кривизни в т.М

Задача. Точка В рухається у площині ху. Закон руху точки заданий рівняннями х=f₁(t), у= f₂(t) ( де х та у виражено у сантиметрах, t- в секундах).

Знайти рівняння траєкторії точки, для моменту часу t₁=2с визначити швидкість та прискорення точки, а також дотичне і нормальне прискорення та радіус кривизни у відповідній точці траєкторії. Закон руху наведено у таблиці 4. Побудувати траєкторії точки у декартової системі координат, знайти положення точки В в заданий момент часу, побудувати вектори швидкості та прискорення.

Таблиця 1-Вихідні дані

№ за списком	Закон руху
	х=f1(t)	у= f2(t)
1,11,21	х=5соs(πt/6)-2	у=3sіn2 (πt/6)
2,12,22	х=соs(πt/6)	у=-8sіn (πt/6)
3,13,23	х= 3-2 соs (πt/6)	у=6соs(πt/3)
4,14,24	х= t-5	у=2t2+2
5,15,25	х=5-2t	у=2-t3
6,16,26	х= 2-t	у=2t3
7,17,27	х= 3t	у=(t+2)2
8,18,28	х=6sіn (πt/6)-2	у=4соs(πt/6)
9,19,29	х=10sіn (πt/6)	у=6соs(πt/6)
10,20,30	х=5-4sіn (πt/6)	у=-3соs(πt/6)

При визначенні траєкторії слід застосовувати відомі тригонометричні формули:

соs(2α)=1- sіn²(α)= 2соs²α-1, sіn(2α)= 2 sіnα ·соsα, sіn²α +соs²α=1.

Питання для самоконтролю.

1. Як визначати швидкість та прискорення при координатному способі завдання руху?

2. Як визначається повне прискорення?

3. Як визначити радіус кривизни траєкторії?