4 Самостійна робота 3

Тема: Визначення центру ваги плоских фігур складної форми

Питання, що розглядаються

1 Статичний момент площі. Головні осі

2. Центр ваги простих фігур

3. Визначення координат центру ваги фігур складної форми

До самостійної роботи слід приступати після вивчення теми «Центр ваги», з'ясувавши поняття про статичний момент відносно осі і розгляду прикладу. Студенти набувають навичок визначення центру ваги складних перерізів, що в подальшому необхідно для вирішення багатьох задач статики та опору матеріалів (тема геометричні характеристики перерізів).

Статичним моментом перерізу відносно даної осі називають взяту по всій площі перерізу суму добутків площинок dА на їхні відстані до даної осі

(рисунок 1):

(1)

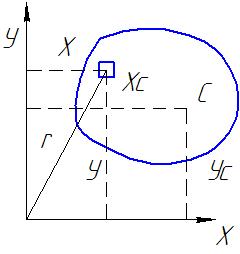
Рисунок 1-До визначення статичного моменту

Статичний момент перерізу може бути додатним, від'ємним або дорів­нювати нулю. Розмірність статичного моменту - мм³ або м³. Знаючи статичні моменти, можна розрахувати координати центру ваги перерізу:

(2)

де А-площа перерізу. В випадку наявності у перерізі отворів, застосовують "метод негативних площ" (таким площам в формулах 2 умовно надається знак «мінус»).

Осі, що проходять через центр ваги перерізу називають центральними.

Варто зауважити, що центр ваги симетричних перерізів,що мають дві осі симетрії, лежить на перетину осей симетрії: паралелограма - на перетину діагоналей, якщо переріз має одну вісь симетрії, то центр ваги лежить на цій осі і потрібно розрахувати лише одну координату, у трикутника - на перетині медіан на відстані

1/3 висоти від його основи. У додатку 1 наведені дані щодо координат центру ваги деяких плоских перерізів.

Рекомендується наступна послідовність рішення задач на визначення координат центру ваги перерізу:

1) накреслити переріз у обраному масштабі;

2) обрати осі координат Х та У;

3) розбити складний переріз на прості фігури, застосовуючи у випадку необхідності "метод негативних площ";

4) визначити положення центрів ваги простих фігур в обраній системі координат;

5) розрахувати площі простих фігур;

6) розрахувати статичні моменти простих фігур;

7) визначити координати центру ваги складного перерізу.

Приклад. Для заданої плоскої фігури (тонкої однорідної пластини) визначити положення центру ваги. Розміри на кресленні задані в сантиметрах.

Розв’язок. Визначення положення центру ваги фігури означає визначення координат її центру ваги у вибраній системі координат. Дану складну фігуру уявляємо складену із трьох простих: І - прямокутника, II - кола, III - трикутника. Площі колового і трикутникового отворів вводимо в розрахунок зі знаком мінус, а площу прямокутника - без врахування отворів, які є в ньому.

Площі простих фігур:

прямокутника А1= 12 ·31 =372 см²;

кола А₂= 78,5 см²;

трикутника Аз = -12 ·9 / 2 = - 54 см², де співпадаюча з віссю симетрії висота трикутника H= 31 - (8 + 10/2 + 6)=12 см.

Фігура має вісь симетрії, тобто її центр ваги лежить на цій вісі. Сполучаємо координатну вісь х з віссю) симетрії, а початок координат - з лівим краєм фігури (щоб координати центрів ваги були позитивними).

Координати центра ваги простих фігур: ·х₁=31 / 2 = 15,5 см; х₂ = 8 см; х_з = 31 - 6 - 12/3=21см, де 12 / 3 см - відстань від центру ваги трикутника до його основи, дорівнює 1/3 висоти H.

Координати центра ваги заданої плоскої фігури

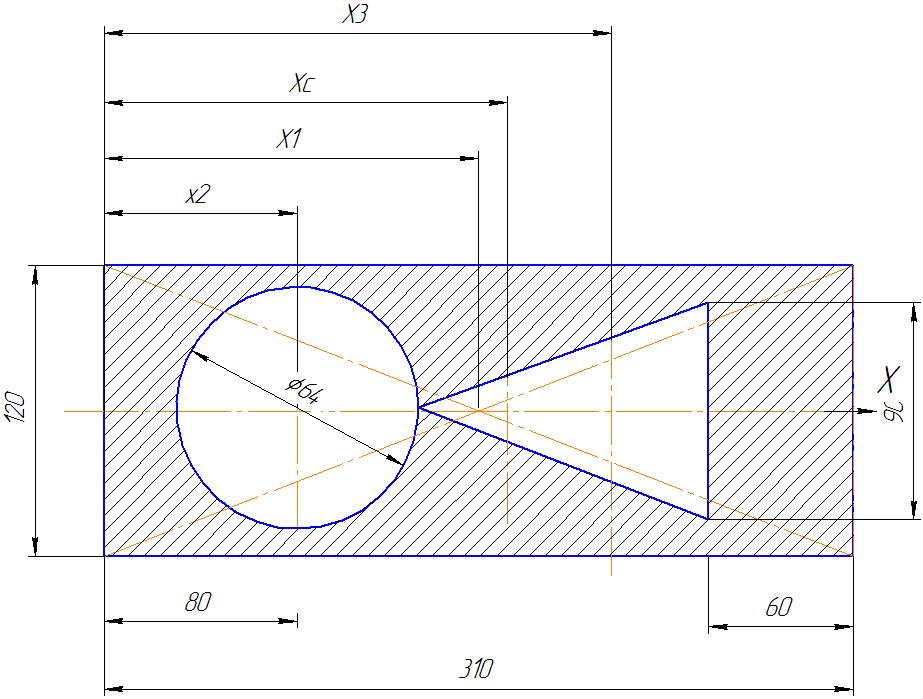
Рисунок 2- Розрахункова схема перерізу

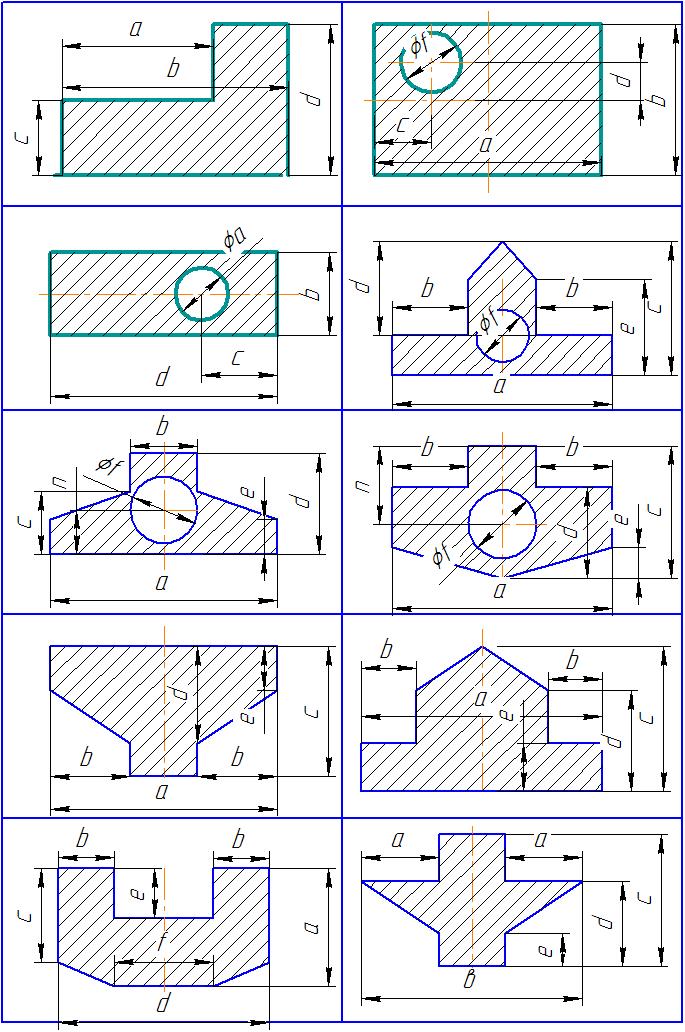
Таблиця 1-Вихідні дані

Варіант	№ схеми	а,мм	в, мм	с, мм	d,мм	е, мм	f, мм	n, мм
1	1	40	60	20	50	-	-	-
2	2	20	40	30	80	-	-	-
3	3	90	30	30	60	16	20	20
4	4	100	30	80	60	20	-	-
5	5	80	20	40	120	20	-	-
6	6	140	60	30	20	-	18	-
7	7	140	40	80	60	60	20	-
8	8	90	20	90	60	20	20	-
9	9	110	30	80	60	80	20	-
10	10	30	100	80	60	20	-	-
11	1	42	66	24	53	-	-	-
12	2	18	44	32	88	-	-	-
13	3	94	34	30	62	14	18	18
14	4	110	30	82	58	18	-	-
15	5	88	20	44	120	22	-	-
16	6	120	50	20	18	-	18	-
17	7	144	42	82	62	58	20	-
18	8	96	24	92	58	20	20	-
19	9	104	28	78	60	78	20	-
20	10	32	110	78	56	20	-	-
21	1	41	66	22	53	-	-	-
22	2	19	44	30	88	-	-	-
23	3	95	34	31	62	14	18	18
24	4	112	30	78	58	18	-	-
25	5	86	20	42	120	22	-	-
26	6	122	50	22	18	-	18	-
27	7	148	42	81	62	58	22	-
28	8	98	24	93	58	20	21	-
29	9	110	28	75	60	78	24	-
30	10	36	110	73	56	20	-	-

Питання для самоперевірки.

1. Чому дорівнює статичний момент перерізу відносно центральних осей?

2. Запишіть формули визначення координат центра мас плоского довільного перерізу, для перерізу що має одну вісь симетрії.