17 Самостійна робота №16

Тема: Побудова планів швидкостей і прискорень кулісних механізмів

Питання, що розглядаються

1. Призначення та структура кулісних механізмів

2. Особливості визначення кінематичних параметрів кулісних механізмів

3. Розв’язування задачі.

Кулісні механізми достатньо широко представлені в техніці, зокрема в приводах верстатів, де обертовий рух перетворюється в зворотно-поступальний рух-стругальні, довбальні, плоскошліфувальні верстати та інші. Кулісою називається рухома направляюча, яка здійснює обертовий рух (коливальний). Схема кулісного механізму наведена на рисунку 1.

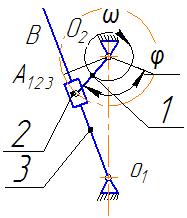
Рисунок 1-схема кулісного механізму

1-кривошип, 2-повзун (кулісний камінь), 3-куліса.

Особливість кінематичного розрахунку кулісних механізмів полягає в тому, що кулісний камінь здійснює складний рух, причому в якості переносного руху маємо обертовий рух куліси. Тоді абсолютне прискорення дорівнює векторної сумі переносного, відносного та Коріолісова прискорень.

Приклад. В кулісному механізмі О₂А=100мм, О₁О₂=245мм, кутова швидкість ведучої ланки ω=12с^-1. Визначити швидкість точки В куліси в заданому положенні механізму при φ=30°.

Розв’язок.

Креслимо план кулісного механізму в масштабі

Визначаємо швидкість точки А в обертовому русі навколо точки О₁:

Точка А₃ здійснює складний рух, який складається з переносного руху разом з кулісою 3 та відносного руху вздовж куліси. З іншого боку, швидкість точки А₃ можна розглянути як векторну суму швидкості полюсу V_О1 та швидкості обертання точки А3 навколо точки О1- V_А3О1.

Швидкість точки А₃ куліси, яка співпадає із швидкістю кулісного каменю А2 визначається з векторних рівнянь:

V_А3= V_О1+ V_А3О1 (1)

V_А3= V_А1+ V_А1А3 (2)

- швидкість точки А3 куліси в обертовому русі відносно точки О1.

- швидкість точки А2 каменю в поступальному русі відносно точки А3 куліси.

В цих рівняннях швидкість V_А1 відома за величиною та напрямком, V_О1=0. Відносні швидкості V_А3О1 та V_А1А3 відомі лише за лінією напрямку: V_А3О1 спрямована перпендикулярно до ланки 3в заданому положенні,

а вектор швидкості V_А1А3 спрямований вздовж ланки 3. Тому для визначення швидкості точки розв’язуємо систему рівнянь (1), (2) графічним способом (методом побудови плану швидкості).

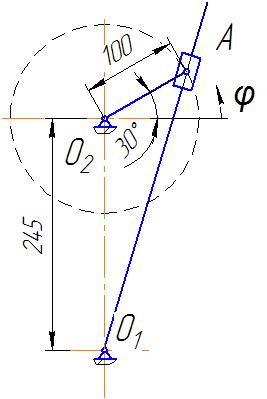
Рисунок 2- схема кулісного механізму в масштабі

Креслимо план швидкостей. Для цього задаємося довжиною відрізка ра, який буде зображувати на плані швидкостей швидкість точки V_А, розраховуємо масштаб плану швидкостей

від довільної точки р, яку прийнято за полюс, відкладаємо перпендикуляр до ланки 1 в напрямку обертання і ньому відрізок ра=60мм.

Через точку а плану швидкостей (кінець вектора ра) проводимо лінію, яка паралельна до ланки 3, а через полюс р лінію, яка перпендикулярна ланці 3. На перетину цих напрямків отримаємо точку в - кінець вектора абсолютної швидкості точки А3 куліси.

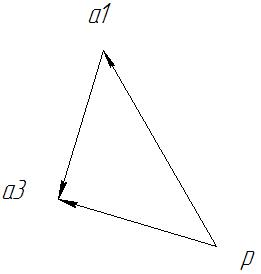
Рисунок 3 – план швидкостей кулісного механізму в масштабі

З плану швидкостей визначаємо:

V_A3=ра₃·μ_v=43,6·0,02=0,872м/с

Визначаємо прискорення точки А₁:

Прискорення точки А3 куліси можна знайти, розв’язавши систему векторних рівнянь шляхом побудови плану прискорень

(3)

(4)

В рівняннях (3), (4)

прискорення нерухомої точки стійки;

нормальне прискорення точки А3 навколо точки О1,

Для плану прискорень вибираємо довжину відрізка πа=15мм, який зображує прискорення точки А в масштабі μ_а= . В цьому масштабі довжина відрізка, який зображує вектор нормального прискорення

прискорення Коріоліса,

Модуль прискорення Коріоліса дорівнює

де кутова швидкість куліси

Відносна швидкість з плану швидкостей

В обраному масштабі довжина відрізка, який зображує вектор прискорення Коріоліса

Напрямок прискорення Коріоліс визначається напрямком векторного добутку векторів ω і Vr, тобто прискорення Коріоліса буде направлено перпендикулярно площині, що проходить через век­тори ω і Vr, в той бік, звідки найкоротший перехід від ω до видно, що проходять проти ходу стрілки годинника. Або за правилом Жуковського М.Є. про­екцію відносної швидкості V_r на площину, перпендикулярну кутовій швидкості ω слід повернути на кут 90° навколо ω в напрямку обертання.

Будуємо план прискорень.

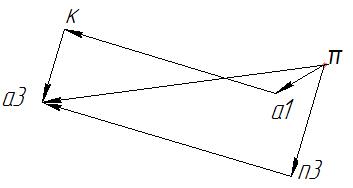
Рисунок 4- План прискорень в масштабі

З плану прискорень визначаємо

Визначаємо кутове прискорення ланки 3

Завдання. Визначити лінійні та кутові швидкості та прискорення точок та ланок кулісного механізму в заданому положенні кривошипу φ.

Таблиця 1-Вихідні дані

Варіант	φ, град	ω1, с-1	О1О2, мм	О2А, мм
1	15	330	350	130
2	20	400	370	120
3	25	300	380	125
4	33	310	400	170
5	65	450	450	150
6	60	500	440	120
7	70	300	410	120
8	200	310	360	100
9	120	430	400	130
10	0	460	430	135
11	190	540	420	120
12	220	390	390	130
13	250	380	370	110
14	270	340	350	120
15	300	440	370	115
16	320	430	380	120
17	180	420	400	130
18	150	350	450	150
19	80	420	440	140
20	90	410	410	140
21	50	470	360	120
22	80	480	400	130
23	260	530	430	135
24	300	520	420	140
25	200	510	390	130
26	170	490	370	120
27	340	420	360	120
28	210	320	400	130
29	290	500	430	140
30	130	480	420	130