
- •1 Загальні методичні вказівки та рекомендації
- •2 Самостійна робота 1
- •3 Самостійна робота 2
- •4 Самостійна робота 3
- •5 Самостійна робота 4
- •6 Самостійна робота 5
- •7 Самостійна робота 6
- •8 Самостійна робота 7
- •9 Самостійна робота 8
- •10 Самостійна робота №9
- •11 Самостійна робота №10
- •12 Самостійна робота №11
- •Шпонки призматичні
- •13 Самостійна робота 12
- •14 Самостійна робота 13
- •15 Самостійна робота №14
- •11) Визначити значення еквівалентного моменту за ііі та іv гіпотезою міцності:
- •16 Самостійна робота №15
- •17 Самостійна робота №16
- •Питання для самоперевірки.
- •18 Самостійна робота №17
- •Значення e, g та для деяких матеріалів.
- •Механічні характеристики деяких матеріалів
- •Сталь прокатна кутова нерівнобічна (гост 8510-57)
- •Сталь прокатна. Балки двотаврові (гост 8239-56)
- •Сталь прокатна. Швелери (гост 8240-56)
15 Самостійна робота №14
Тема: Розрахунок діаметру вала за різними теоріями міцності
Питання, що розглядаються
Розрахунок вала з умов міцності при складних навантаженнях
Гіпотези міцності
Розв’язування задачі
До
виконання самостійної роботи студенти
приступають після вивчення тем «Складні
види навантаження» та «Поняття про
теорії міцності». Розрахунок на міцність
є однією з найголовніших задач забезпечення
функціональної здатності елементів
машин та споруд в умовах експлуатації.
Оскільки складні види навантаження
зустрічаються в техніці достатньо часто
(наприклад згин і кручення, розтяг і
згин і т.п.), то виникає необхідність
оцінки напруженого стану за еквівалентними
напруженнями для простого одновісного
навантаження. Так, при сумісній дії
кручення та згину розраховують величину
еквівалентного моменту:
![]() або
або
![]() відповідно
за ІІІ та IV
гіпотезами міцності.
відповідно
за ІІІ та IV
гіпотезами міцності.
Завдання. На сталевий вал круглого перерізу насаджено зубчасті колеса 1,2. Вал передає потужність Р (кВт) при кутовій швидкості w (с-1). Визначити найнебезпечніший переріз вала та розрахувати його діаметр за третьою теорією міцності (найбільших дотичних напруг) та четвертою теорією міцності. Прийняти [σ]=160МПа, Fr1=0,4F1, Fr2=0,4F2,
Рекомендована послідовність виконання роботи.
1) Накреслити вал разом з навантаженням;
2) Розрахувати обертовий момент
![]() (кНм)
(кНм)
3) Визначити діючи навантаження
![]() ,
,
![]() ,
Fr1=0,4F1,
Fr2=0,4F2
,
Fr1=0,4F1,
Fr2=0,4F2
4) вибрати розташування координатних осей, поєднавши вісь z з валом, вісь у направивши у вертикальній площині, вісь х в горизонтальній площині, звільнити вал від опор , виконав заміну їх дії реакціями опор, спрямованими вздовж осей координат, скласти рівняння рівноваги статики для довільної плоскої системи сил таким чином і в такій послідовності, щоб рішенням кожного з цих рівнянь було визначення однієї з невідомих реакцій опор, визначити реакції опор у вертикальній та горизонтальній площинах;
5) перевірити
правильність знайдених опорних реакцій
по рівнянню, яке не було використано
для вирішення завдання, (![]() ,
,![]() ).
).
6) Вал поділити на ділянки, границі яких співпадають з точками прикладання сил;
7) За допомогою методу перерізів та розглядаючи рівновагу відрізаної частини валу, скласти рівняння для визначення згинального моменту на ділянках вала у вертикальній Мх та горизонтальній Му площині;
8) Побудувати епюру згинальних моментів в вертикальній Мх та горизонтальній Му площині;
10) Розрахувати максимальний згинальний момент:
![]()
11) Визначити значення еквівалентного моменту за ііі та іv гіпотезою міцності:
12) Розрахувати необхідний діаметр вала:
![]() та
та
![]()
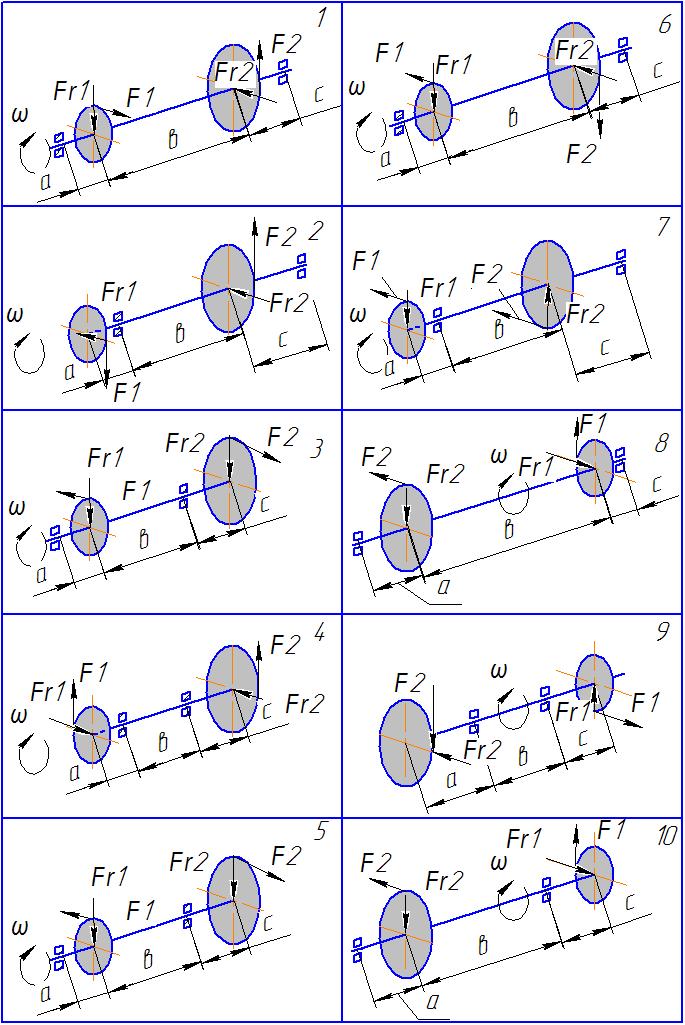
Таблиця 1- Варіанти завдань
Варіант |
№ схеми |
Р, кВт |
ω , с-1 |
D1,мм |
D2,мм |
1 |
1 |
6 |
45 |
120 |
250 |
2 |
3 |
26 |
20 |
58 |
160 |
3 |
3 |
10 |
38 |
80 |
240 |
4 |
4 |
9 |
40 |
140 |
240 |
5 |
5 |
6 |
45 |
120 |
250 |
6 |
8 |
4 |
12 |
40 |
240 |
7 |
7 |
4 |
12 |
40 |
240 |
8 |
10 |
10 |
50 |
125 |
300 |
9 |
9 |
20 |
68 |
120 |
400 |
10 |
7 |
9 |
40 |
58 |
160 |
11 |
6 |
21 |
46 |
80 |
240 |
12 |
8 |
22 |
22 |
58 |
160 |
13 |
9 |
12 |
56 |
120 |
250 |
14 |
1 |
5 |
23 |
80 |
240 |
15 |
10 |
36 |
70 |
140 |
280 |
16 |
3 |
10 |
24 |
60 |
180 |
17 |
2 |
3 |
25 |
60 |
180 |
18 |
5 |
8 |
24 |
150 |
260 |
19 |
4 |
64 |
38 |
140 |
280 |
20 |
5 |
10 |
38 |
80 |
240 |
21 |
4 |
80 |
25 |
30 |
250 |
22 |
7 |
18 |
16 |
60 |
180 |
23 |
6 |
12 |
28 |
40 |
240 |
24 |
9 |
5 |
48 |
150 |
260 |
25 |
8 |
50 |
24 |
120 |
400 |
26 |
1 |
10 |
32 |
140 |
240 |
27 |
10 |
34 |
43 |
130 |
250 |
28 |
3 |
22 |
30 |
125 |
300 |
29 |
2 |
10 |
14 |
125 |
300 |
30 |
8 |
48 |
38 |
120 |
250 |
Приклад.
Для
стального валу постійного поперечного
перерізу з двома зубчатими колесами,
який передає потужність Р при кутової
швидкості ω визначити діаметр вала по
двох варіантах, використовуючи третю
та п’яту гіпотези міцності, Р=10кВт,
![]() [σ]=180МПа,
Fr1=0,4F1,
Fr2=0,4F2,
[σ]=180МПа,
Fr1=0,4F1,
Fr2=0,4F2,
![]()
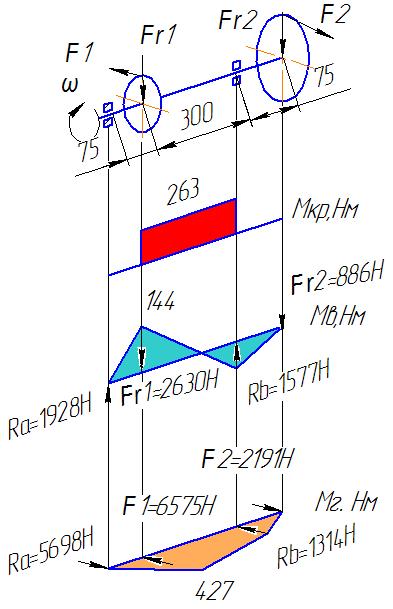
Розв’язок.
Розраховуємо обертовий момент
![]() (Нм)
(Нм)
Визначаємо діючи навантаження
![]() ,
,
![]() ,
Fr1=0,4F1=0,4·6575=2630Н,
Fr2=0,4F2=0,4·2191=876Н
,
Fr1=0,4F1=0,4·6575=2630Н,
Fr2=0,4F2=0,4·2191=876Н
Визначаємо невідомі реакції опор у вертикальній та горизонтальній площинах.
Вертикальна площина:
![]()
![]() ,
,
звідси
![]()
![]()
![]() ,
звідси
,
звідси
![]() ,
перевірка:
,
перевірка:
![]()
Максимальний
момент
![]()
Горизонтальна площина:
![]() ,
звідси
,
звідси
![]()
![]() ,
звідси
,
звідси
![]()
перевірка:
![]()
Максимальний
момент
![]() Розраховуємо максимальний згинальний
момент:
Розраховуємо максимальний згинальний
момент:
![]()
Визначаємо значення еквівалентного моменту за третьою гіпотезою міцності:
![]()
За четвертою гіпотезою міцності:
![]() Необхідні
діаметри валів:
Необхідні
діаметри валів:
![]() ,
,
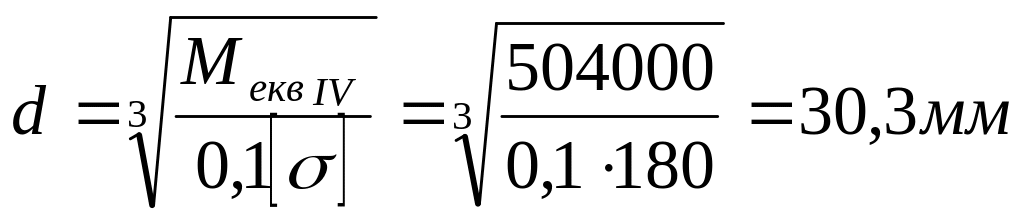
Питання для самоперевірки.
1. Як виконується розрахунок на міцність при одночасній дії кручення та згину?
2. Що таке еквівалентний момент?
3. Як виконати розрахунок на міцність за допомогою еквівалентного моменту?
