11 Самостійна робота №10
Тема: Розтяг-стиск ступеневого брусу
Питання, що розглядаються.
1. Поздовжні сили і їх епюри.
2. Нормальні напруження в поперечних перерізах бруса і епюри нормальних напружень. Повздовжні деформації. Визначення переміщень поперечних перерезів.
3. Розв’язування задач
Розтягом (стиском) називають такий вид деформування стержня, коли зовнішні сили діють уздовж його осі, а в його поперечних перерізах виникають тільки поздовжні зусилля N.
З умов рівноваги розділених частин стержня випливає, що внутрішнє зусилля N дорівнює зовнішній силі F, тобто N=F. Для знаходження напружень в поперечному перерізі стержня площею А використовується вираз:
(1)
При розтягу (стиску) стержня виникають нормальні напруження, які є причиною лінійної деформації. Відносна деформація з закону Гука:
(2)
Оскільки
то
(3)
Тобто абсолютне видовження (скорочення) стержня прямо пропорційно поздовжньому зусиллю N, довжині стержня l, обернено пропорційно площі перерізу А та модулю пружності матеріалу Е. У випадку, коли стержень має n ділянок, в межах яких Ni та Ai мають постійні значення, повне абсолютне видовження (скорочення)
(4)
Абсолютне видовження необхідно знати для перевірки елементів технічних об’єктів на жорсткість за умовою:
,
(5)
де
допустиме
видовження (скорочення) стержня, яке
визначається за нормативами в залежності
від марки конструктивного матеріалу
та конструктивних особливостей.
При розрахунку на міцність необхідно знати допустимі напруження.
Для елементів механічних об’єктів, що виготовлені з пластичних матеріалів
,
(6)
де S- коефіцієнт запасу міцності відносно границі текучості, S=1,5…2
Малі значення коефіцієнта запасу міцності в даному випадку пояснюються тим, що виникнення можливого явища текучості в матеріалі деталі не спричинить раптового і повного її руйнування.
Для статично навантажених елементів технічних об'єктів, виготовлених з крихких матеріалів, за граничне напруження приймають границю міцності матеріалу σв. В даному випадку допустиме напруження
У розрахунках деталей з крихких матеріалів коефіцієнти запасу міцності призначають в межах [S]=2,5...3. Тут підвищені коефіцієнти запасу міцності обґрунтовуються тим, що крихкі матеріали руйнуються раптово.
Задача 1. Визначити розміри перерізу сталевого квадратного бруса а×а довжиною L за умовою, що абсолютне видовження під навантаженням F склало величину Δl. Визначити площу перерізу деформованого брусу, якщо коефіцієнт Пуассона μ. Модуль Юнга прийняти 2·105 Н/мм2
Таблиця 1- Вихідні дані до задачі 1
-
Варіант
F, кН
L, мм
Δl, мм
μ
1
40
1100
1,1
0,28
2
20
2000
0,8
0,25
3
100
2300
3,0
0,33
4
60
2500
2,1
0,3
5
55
2200
2,2
0,27
6
38
1400
1,4
0,26
7
62
2000
2,0
0,29
8
48
1800
1,8
0,31
9
61
2800
2,2
0,32
10
58
1900
1,9
0,28
Задача 2
Двохступенчастий сталевий брус навантажено силами F1, F2, F3. Побудувати епюри поздовжних сил і нормальних напружень по довжині бруса. Визначити переміщення вільного кінця бруса при Е=2·105Н/мм2. Виконати розрахунок на міцність та жорсткість, прийнявши [σ]=160МПа, [Δl]=1,5мм.
Таблиця даних до задачі 2
Варіант |
F1 |
F2 |
F3 |
A1 |
A2 |
кН |
кН |
кН |
см2 |
см2 |
|
1 |
30 |
10 |
5 |
1,8 |
3,2 |
2 |
32 |
16 |
9 |
1,0 |
2,2 |
3 |
17 |
14 |
8 |
1.0 |
2,7 |
4 |
14 |
16 |
11 |
1,7 |
2,6 |
5 |
27 |
15 |
9 |
1,6 |
3,2 |
6 |
23 |
11 |
12 |
1,8 |
4,0 |
7 |
17 |
12 |
21 |
2,4 |
3,8 |
8 |
25 |
13 |
7 |
2,3 |
1,9 |
9 |
37 |
16 |
6 |
2,2 |
1,7 |
10 |
31 |
23 |
5 |
2.0 |
2,6 |
Приклад.
Для даного бруса круглого перерізу, який закріплено одним кінцем і навантажено прикладеними силами, побудувати епюру повздовжніх сил та визначити діаметр кожної ділянки. Для матеріалу бруса ст.3 прийняти [σр]=160МПа, [σс]=120МПа. Визначити деформацію бруса при постійному по довжині перерізі А=2см2.
F1=15кН, F2=7кН, F3=3кН, L1=0,9м, L2=0,9м, L3=0,3м.
Розв’язок.
У даного бруса 3 ділянки: І,ІІ,ІІІ. Для визначення поздовжніх сил на кожній ділянці застосовуємо метод перерізів, починаючи з вільного кінця.
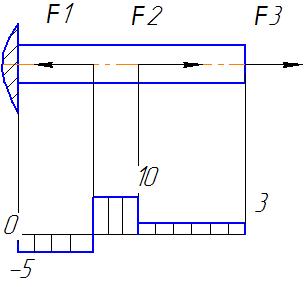
N1=F3=3кН, N2=F3+F2=3+7=10кН, N3=F3+F2-F1=3+7-15=-5кН. Будуємо епюри поздовжніх сил, причому при розтягу брусу силу вважаємо додатною.
Визначаємо площі перерізів ділянок з умови міцності:
Далі визначаємо діаметри круглого бруса на кожній ділянки:
Визначаємо деформацію бруса при постійному перерізі А=2см2.
Загальна деформація бруса:
Питання для самоперевірки
1. Що називається напругою?
2. Що таке деформація?
3. Який вид напружено-деформованого стану називається розтягом (стиском)?
4. Як розрахувати видовження (скорочення) довжини стержня під дією зовнішньої сили?
5. Як визначаються нормальні напруження при розтягу-стиску?
6. Як виконується розрахунок на міцність і жорсткість при розягу-стиску?