Вінницький транспортний коледж

ПРИКЛАДНА МЕХАНІКА

Завдання для виконання самостійних робіт з методичними вказівками для студентів спеціальності 5.05050204 «Експлуатація та ремонт підйомно-транспортних, будівельних і дорожніх машин і обладнання»

Вінниця

2013

Завдання для виконання самостійних робіт з методичними вказівками з дисципліни «Прикладна механіка».

Розробник викладач Беньковський В.І.

Розглянуто і схвалено цикловою комісією спеціальності 5.05050204

Протокол №_____ від________

Голова циклової комісії___________В.І.Підлісний

Зміст

1	Загальні методичні вказівки та рекомендації	4
2	Самостійна робота 1	5
3	Самостійна робота 2	14
4	Самостійна робота 3	25
5	Самостійна робота 4	30
6	Самостійна робота 5	35
7	Самостійна робота 6	39
8	Самостійна робота 7	47
9	Самостійна робота 8	51
10	Самостійна робота 9	55
11	Самостійна робота 10	65
12	Самостійна робота 11	71
13	Самостійна робота 12	74
14	Самостійна робота 13	80
15	Самостійна робота 14	88
16	Самостійна робота 15	94
17	Самостійна робота 16	98
18	Самостійна робота 17	104
19	Додатки	110

1 Загальні методичні вказівки та рекомендації

Самостійна робота студента при вивченні дисципліни «Прикладна механіка» займає важливе місце.

Виконання самостійних робіт пов’язано із розв’язанням варіантів прикладних задач за темами та відповідями на теоретичні питання для самоперевірки. До виконання самостійних робіт студенти приступають після вивчення конспекту лекції з відповідної теми, виконання практичної роботи та опрацювання рекомендованої літератури. Таким чином, кожна самостійна робота закріплює теоретичний матеріал та практичні навички, спонукає до індивідуальної творчої роботи.

Структура кожної роботи складається з теми, переліку питань, що розглядаються, теоретичних відомостей, прикладу розв’язку задач, завдання для самостійного виконання, питань для самоперевірки та літературних джерел. Варіанти практичних задач індивідуальні та відповідають порядковому номеру в списку навчальної групі або останній цифрі. Самостійні роботи більш доцільно виконувати на форматі А4 як більш зручному для виконання розрахункових схем та оформлення розрахунків відповідно стандарту щодо текстової документації. В додатках наведені довідкові дані для розв’язання практичних задач.

2 Самостійна робота 1

Тема: Визначення реакцій ідеальних в’язів (типу стержень та нитка) аналітичним і графоаналітичним способом

Питання, що розглядаються

1. Аксіома в’язів

2. Проекція сили на вісь

3. Умова рівноваги плоскої системи збіжних сил

Статика, розглядаючи рівновагу системи діючих на тіло сил, дає правила для визначення вхідних в цю систему невідомих сил (звичайно це реакція зв'язків, а визначенню можуть підлягати і деякі активні сили). Знання модулів і направлень всіх діючих на тіло сил необхідно при виконанні більшості технічних розрахунків, які розглядаються в наступних розділах курсу технічної механіки.

Нагадуємо, що при розгляданні рівноваги тіла накладені на нього зв'язки потрібно відкинути, замінивши їх дію реакціями (тобто силами дії зв'язків на тіло. В цьому і полягає аксіома в’язів). Реакція гнучкого зв'язку (трос, нитка і т.д.) направлена вздовж зв'язку в сторону від тіла. Гнучкий зв'язок, перекинутий через блок, міняє направлення сили, що передається, без зміни її модуля. Реакція ідеального стрижня з шарнірно закріпленням кінців направлена вздовж його вісі в сторону від тіла (якщо стрижень навантажений силою) або в сторону до тіла (якщо це сила стиску).

До виконання самостійної роботи необхідно приступати після вивчення тем "Основні поняття і аксіоми статики" і «Плоска система збіжних сил» з'ясування приведених нижче методичних вказівок і розгляду прикладів.

В запропонованих задачах розглядається тіло, (точка), яка знаходиться в рівновазі під дією плоскої системи сил, які сходяться в одній точці. При аналітичному методі рішення застосовувана система двох рівнянь рівноваги має вигляд та (сума проекцій сил системи на кожну із координатних осей дорівнює нулю). В учбовій літературі застосовується і інша форма запису цих же рівнянь:

X_i= 0; Y_i=0. Слід пам’ятати, що проекція сили на вісь дорівнює добутку модуля сили на косинус її гострого кута з віссю. Знак проекції визначається збігом направлень проекції і вісі. Слід звернути увагу на можливість спростити рішення подібних задач шляхом раціонального вибору направлення координатних осей.

Розв'язавши задачу аналітичним методом, необхідно потім перевірити правильність розв'язку за допомогою графоаналітичного методу методом побудови плану сил, тобто графічної інтерпретації векторного рівняння рівноваги .

Приклад. Визначити сили реакції стержнів АВ і АС кронштейну, який тримає в рівновазі грузи F₁ = 6кН і F₂=2кН (рисунок 1). Вагою частин конструкції, а також тертям на блоці знехтувати.

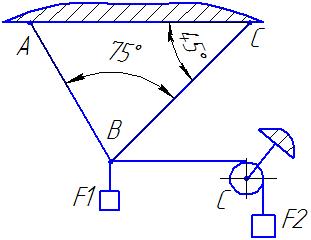
Рисунок 1- схема кронштейна

Розв’язок. Задачу розв'язуємо аналітичним методом. Розглядаємо рівновагу точки (вузла) А. (рисунок 2).

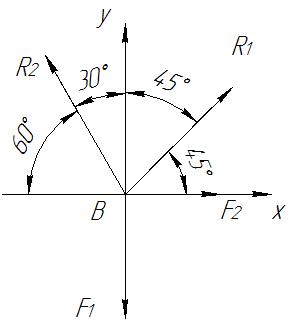
Рисунок 2 –Схема сил, що діють на вузол В (варіант 1)

До неї задані активні сили - сила натягу тросу, яка дорівнює вазі вантажу F₁, та сила тяжіння вантажу F₂. Ці сили направлені від точки В. Відкидаємо зв'язки (стрижні АВ і ВС), замінюючи їх дію реакціями R1 та R2. Реакції стрижнів направляємо від точки В, так як попередньо покладаємо, що стержні розтягнуті (дійсне направлення реакцій стержнів на початку розв'язку невідоме). Якщо наше припущення буде не вірним, то знайдена реакція стержня буде мати знак « мінус»; а це говорить про те, що стрижень зжатий і дійсне направлення реакції — до точки В. Одержана розрахункова схема показана на рисунку 2, варіант 1.

Приймаємо звичайне вертикально-горизонтальне направлення координатних вісій. Для одержаної плоскої системи сил, які сходяться, складаємо два рівняння рівноваги:

або та (1)

, або (2)

Розв'язуючи одержану систему рівнянь, знаходимо R1=5,86кН і R2=-4,34кН. Знак «-» показує, що стержень ВС стиснутий.

Потрібно відзначити, що кожне із одержаних рівнянь рівноваги має по дві невідомі, чого можна було уникнути, якби направити координатні вісі по-іншому - якщо сполучити одну із вісій з невідомою силою, наприклад R2. При цьому в рівнянні рівноваги для вісі залишиться лише одне невідоме:

або (3)

або (4)

звідки R₁=5,86кН і R₂=-4,34кН.

Для перевірки правильності розв'язку застосовуємо графічний метод.

В обраному масштабі будуємо замкнутий силовий багатокутник, тобто графічне зображення векторного рівняння:

(5)

Для цього від довільної точки відкладаємо вектор заданої сили F1(60мм) та від кінця вектора F₁- вектор заданої сили F₂ (20мм.).

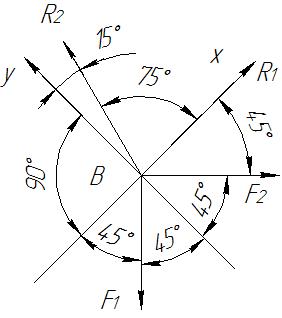
Рисунок 3- Схема сил, що діють на вузол А (варіант 2)

Потім через початок вектора F₁ і кінець вектора F₂ проводимо відомі направлення реакцій R₁ та R₂ стержнів АВ і АС. Вимірюючи знайдені вектори, з врахуванням прийнятого масштабу одержуємо R₁=5,9кН і R₂=4,3кН (точність графічного рішення тим вища, чим більше прийнятий масштаб побудови). Необхідно відзначити, що векторний багатокутник показує дійсний, а не передбачений напрямок знайдених сил.

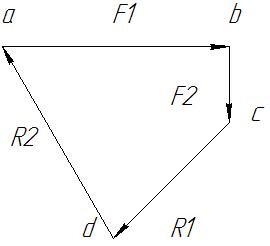
Рисунок 4- план сил в масштабі

Питання для самоперевірки.

1. Як спрямовані реакції ідеальних в’язей типу стержень, нитка?

2. Запишіть умову рівноваги системи збіжних сил у векторній формі та у проекціях.

3. При якому значення кута між силою та віссю проекція сили дорівнює нулю?

4. Наведіть приклад системи збіжних сил у техніці.

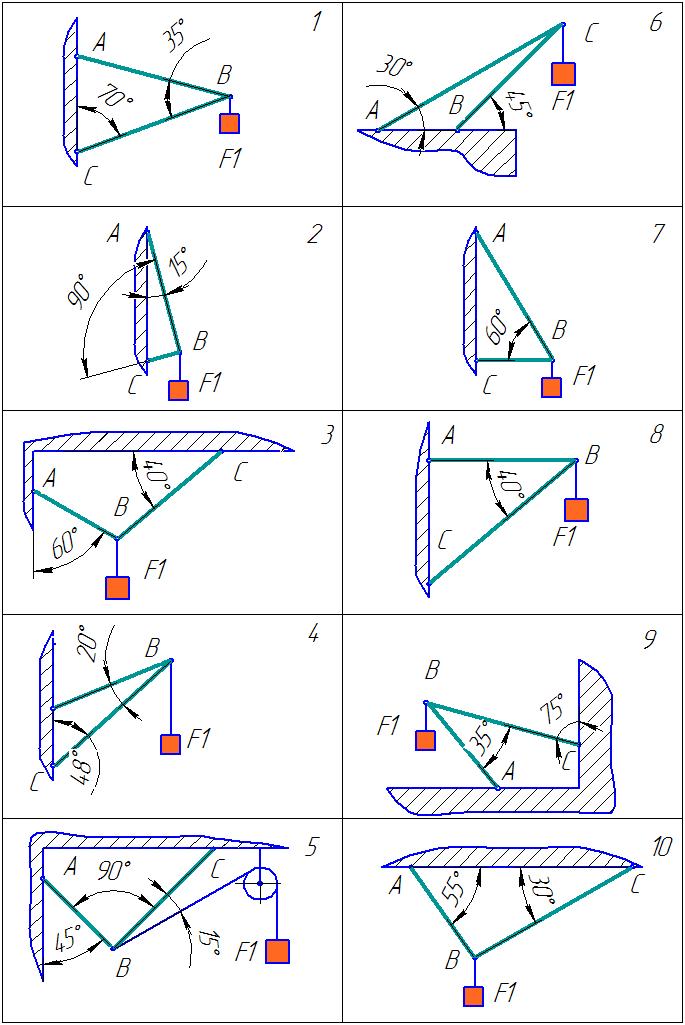
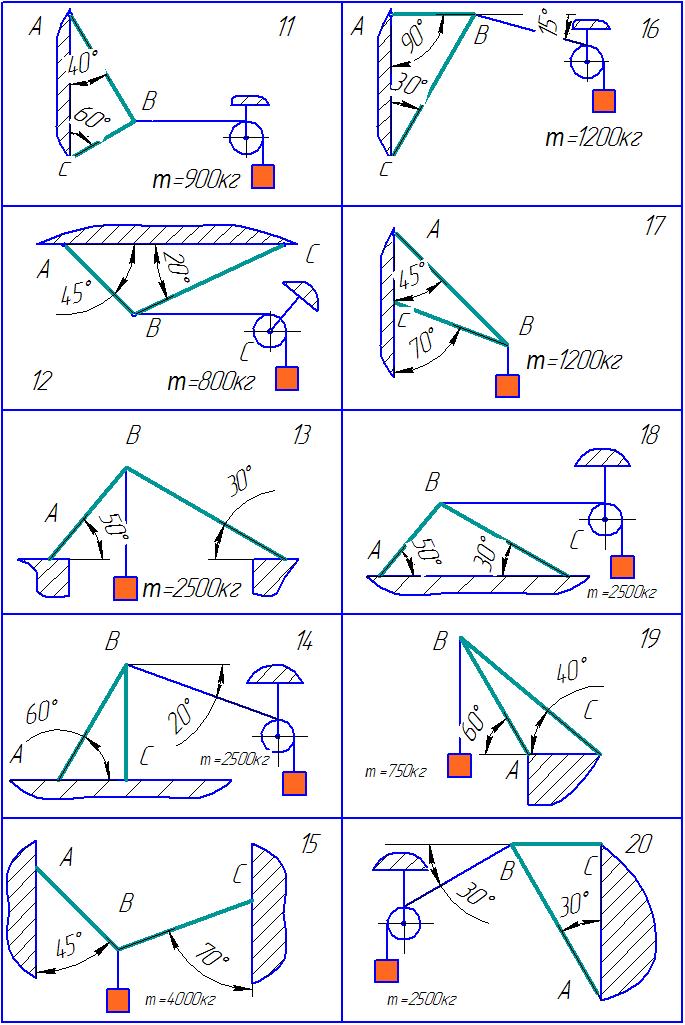
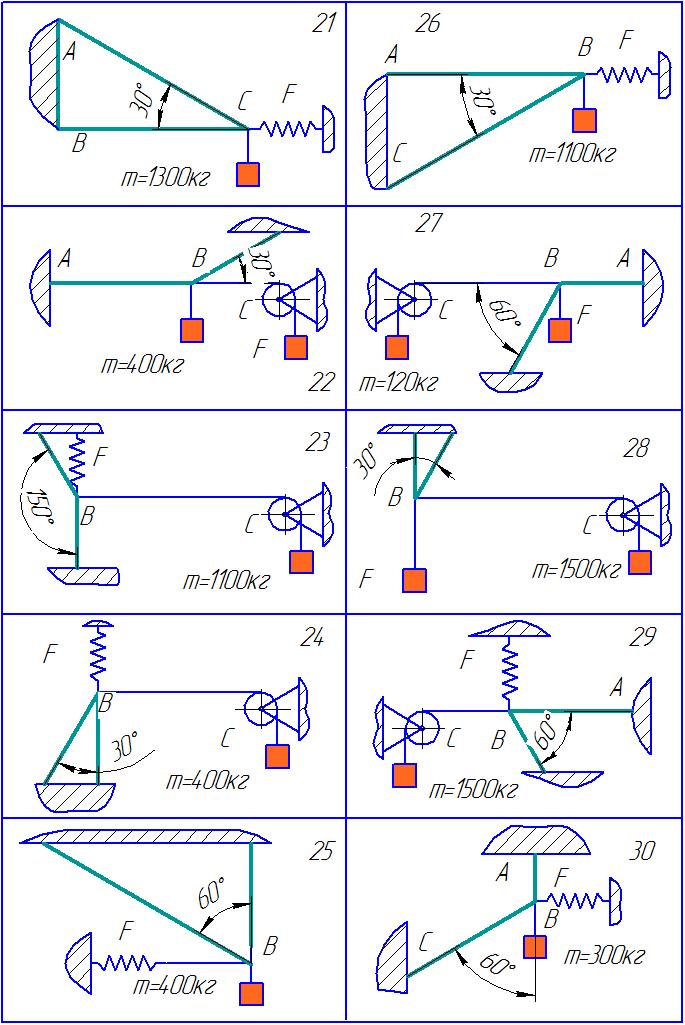
Задача. Визначити сили реакції стержнів кронштейну, який тримає в рівновазі вантаж F₁ або масу m. Вагою частин конструкції, а також тертям на блоці знехтувати. Прийняти .

Таблиця 1- Варіанти завдань

Варіант	№ схеми	F, Н
1	1	5000
2	2	50000
3	3	10000
4	4	50000
5	5	20000
6	6	4000
7	7	1500
8	8	1800
9	9	20000
10	10	1500
11	11	5000
12	12	9000
13	13	7000
14	14	16000
15	15	10000
16	16	5000
17	17	7000
18	18	3000
19	19	9000
20	20	8000
21	1	1000
22	2	2000
23	3	1200
24	4	1800
25	5	3500
26	6	4200
27	7	2400
28	8	800
29	9	900
30	10	700