4. Задание физических свойств

4.1. Первоначально задача раздела 1.6 содержала две среды – воздух и землю и два электрода из однородного материала. В такой постановке модель в ELCUT должна содержать три замкнутых блока соответствующих среде (воздуху), первому и второму электродам. Как среду землю в данном случае учитывать не приходится, следует определить лишь граничное условие на ее поверхности, которое задается на соответствующем нижнем ребре (см. далее). Упрощение посредством замены стержневых электродов струнами привело к тому, что модель в ELCUT должна содержать только один блок, соответствующий среде - воздуху.

4.2. Присвоим мнемоническое имя “Воздух” для метки блока и зададим свойства среды, для чего дважды щелкнем левой кнопкой мыши (в режиме выделения) на области, ограниченной ребрами, созданными в пункте 1.3. Блок станет выделенным и появится диалоговое окно “Свойства выделенных объектов”. Щелкнув левой кнопкой мыши в графе “Метка”, вводим с клавиатуры имя метки – Воздух (рис. 2.16). В ELCUT возможно присвоение меткам как англоязычных, так и русскоязычных названий. Шаг дискретизации оставляем “Автоматический”. Выбираем “OK”, чтобы завершить диалог. В окне “дерева” задачи, раздел “Физические свойства”, подраздел “Метки блоков” появляется элемент “Воздух”.

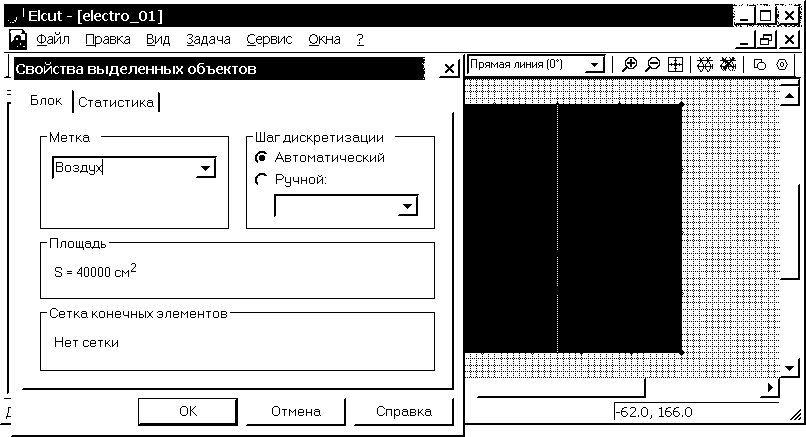
Рис. 2.16. Назначение имени (метки) выделенному блоку расчетной области

4.3. Дважды щелкнув левой кнопки мыши на элементе “Воздух”, открываем окно “Свойства метки блока - Воздух”. В разделе “Диэлектрическая проницаемость” выбираем графу и вводим с клавиатуры – 1. Так как пункт “Анизотропный диэлектрик” не выбран, в графе автоматически появляется 1. Оставляем выбранным пункты: “Относительная” раздела “Диэлектрическая проницаемость” и “Декартовы” раздела “Координаты”. Плотность электрического заряда r оставляем равной нулю (рис. 2.17).

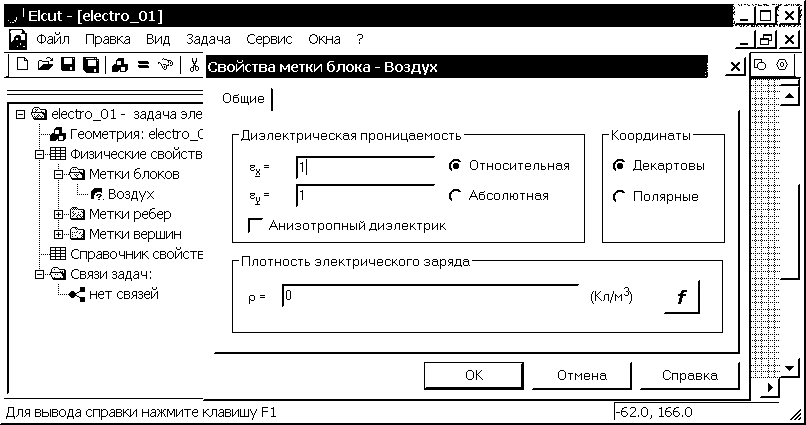
Рис. 2.17. Назначение физических свойств блока с меткой Воздух

Выбираем “OK”, чтобы завершить диалог. Свойства среды в модели теперь полностью определены.

5. Создание меток ребер и вершин

5.1. Щелкнем левой кнопкой мыши на окне геометрической модели, чтобы сделать его активным. Создадим метку для верхнего ребра квадрата, ограничивающего расчетную область. В режиме выделения, дважды щелкнем левой кнопкой мыши на верхнем ребре. Также можно щелкнуть на ребре один раз, после чего нажать комбинацию клавиш Alt+Enter. Появляется окно “Свойства выделенных объектов”. Щелкнув левой кнопкой мыши в графе “Метка”, вводим с клавиатуры имя метки – Поле. Шаг дискретизации оставляем “Автоматический”. Выбираем “OK”, чтобы завершить диалог (рис. 2.18). В окне “дерева” задачи, раздел “Физические свойства”, подраздел “Метки ребер” появляется элемент “Поле”.

Рис. 2.18. Назначение имени (метки) верхнего ребра – Поле. (Аналогично нижнего ребра - Земля)

Аналогично создаем метку “Земля” для нижнего ребра квадрата, ограничивающего расчетную область.

5.2. Для присвоения метки вершине соответствующей верхнему электроду, в режиме выделения дважды щелкнем на ней левой кнопкой мыши. Появляется окно “Свойства выделенных объектов”. Щелкнув левой кнопкой мыши в графе “Метка”, вводим с клавиатуры имя метки – Потенциал 1. Шаг дискретизации оставляем “Автоматический”. Выбираем “OK”, чтобы завершить диалог. В окне “дерева” задачи, раздел “Физические свойства”, подраздел “Метки вершин” появляется элемент “Потенциал 1”.

Аналогично создаем метку с названием “Потенциал 2” для вершины соответствующей нижнему электроду (рис. 2.19). Знаки вопроса около меток ребер и вершин в окне “дерева” задачи указывают на то, что граничные условия на соответствующих элементах еще не определены.

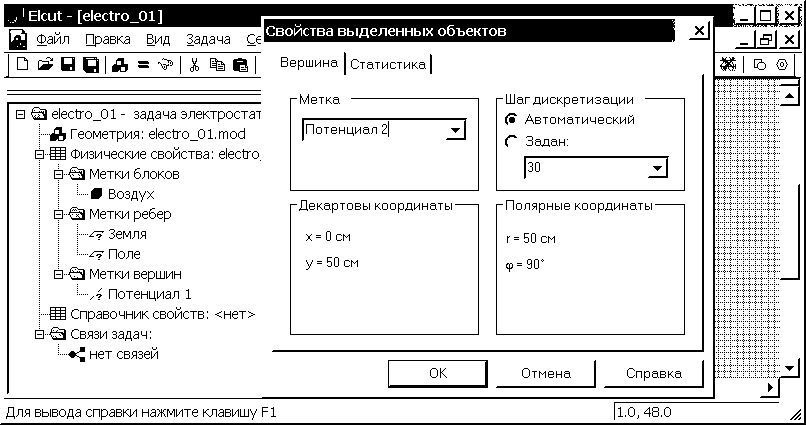
Рис. 2.19. Задание имен (меток) вершин электрических осей электродов: верхнего - Потенциал 1, нижнего - Потенциал 2

Создание меток ребер и вершин закончено, теперь можно задавать граничные условия.