24. Потенциальные поля

Рассмотрим элементарное перемещение dr тела под действием внешних сил

Б удем считать, что силы, действующие на тело при его движении, в любой точке пространства удовлетворяют условию: 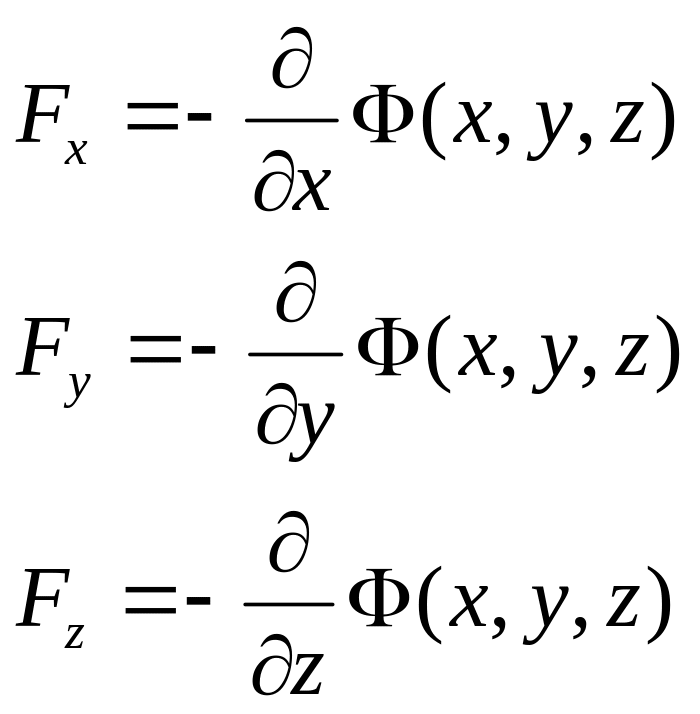(условие 1) где Φ(x,y,z) - некоторая скалярная функция

Т огда

Т аким образом, элементарная работа δA в силовом поле, удовлетворяющем условию (1), равна полному дифференциалу (с обратным знаком) некоторой скалярной функции многих переменных Φ(x,y,z)

Функцию Φ(x,y,z) называют потенциальной функцией силового поля. Силовое поле, удовлетворяющее условию (1), называют потенциальным силовым полем

С войства потенциальных полей

А) для элементарных перемещений: Элементарная работа, совершенная в потенциальном поле над телом, равна дифференциалу (с обратным знаком) потенциальной функции

Б ) на произвольном перемещении:

Работа по перемещению тела в потенциальном поле не зависит от формы траектории, а определяется только начальным и конечным положением тела

С огласно условию (A), при движении по замкнутой траектории . Следовательно Работа в потенциальном поле по любой замкнутой траектории равна нулю.

С иловое поле, удовлетворяющее условию (2), называют консервативным

И мы получаем, что, Если поле потенциально, то оно обязательно консервативно

Консервативное поле не обязательно потенциально

26. Потенциальные поля: оператор «набла», градиент функции….

Выражение можно записать следующим образом: или, что эквивалентно .

В последней формуле выражение в скобках формально является вектором, но его компонентами являются не числа, а некоторые объекты, «желающие взять производные» от функции справа - его называют оператор-вектор.

В физике, оператор-вектор Ñ называют - оператор «набла» действие оператора «набла» на скалярную функцию называют градиентом функции

Градиент функции – это вектор, направленный в сторону быстрейшего возрастания функции

С помощью оператора «набла» выражение - условие потенциальности силового поля - получает более лаконичную форму

В потенциальных полях множество точек поля, в которых потенциальная функция имеет одинаковые значения, называют эквипотенциальной поверхностью

У равнение эквипотенциалей . В потенциальном поле , т.е. сила направлена в сторону убывания потенциальной функции (Φ₁> Φ₂> Φ₃> Φ₄) и следовательно, всегда перпендикулярна эквипотенциальным поверхностям.

Линия, касательная к которой в каждой точке совпадает с направлением силы в этой точке, называется силовой линией. В потенциальном поле силовые линии и эквипотенциальные поверхности всегда взаимно перпендикулярны.

27. Потенциальная энергия

Как мы установили, работа в потенциальном поле равна

Э кспериментально измеримой физической величиной является работа, соответственно, потенциальная функция измерима только с точностью до произвольной константы – т.е., в потенциальном поле любую одну потенциальную поверхность можно принять за поверхность с нулевым значением потенциальной функции Φ₀= 0_. В этом случае работа по перемещению тела из данной точки поля в точку с нулевым потенциалом, численно равна значению потенциальной функции в этой точке

Численное значение потенциальной функции в любой точке поля (при заданном нулевом значении) называют потенциальной энергией тела, находящегося в этой точке

Потенциальная энергия есть мера той работы, которую нужно совершить, чтобы переместить тело из данной точки в точку с нулевым значением потенциальной функции

Учитывая, что потенциальная функция – это способ описания силового воздействия окружающего поля на тело, можно сформулировать следующее качественное определение потенциальной энергии: потенциальная энергия - это мера взаимодействия тела, помещенного в данную точку поля, с окружающим миром.

потенциальная функция потенциальная энергия

(характеристика поля в данной точке) характеристика тела в этой же точке

С ледовательно, для произвольных перемещений в потенциальном поле . Соответственно, для элементарных перемещений .

И выражение (1) – условие потенциальности силового поля - получает еще одну форму