7 .Восстановление уравнения движения (по заданному ускорению)

П усть задан вектор ускорения материальной точки как функция времени

Тогда для dv получим

И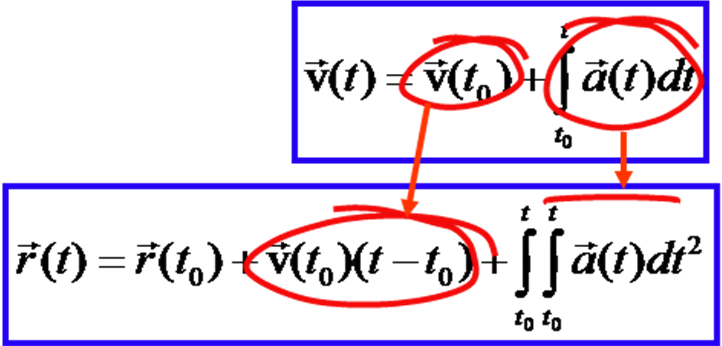 нтегрируя это уравнение в пределах от начального момента времени t₀ до любого текущего t, найдем, где v(t₀) – вектор скорости в начальный момент времени

Теперь, для восстановления уравнения движения воспользуемся предыдущим результатом – получим уравнение траектории по заданной скорости

Таким образом для восстановления уравнения движения по заданному ускорению необходимо знать два параметра: начальное положение материальной точки и скорость в начальный момент времени

8.Преобразование Галилея

Возникает вопрос: как, получить описание движения частицы в СО K, имея результаты измерений, проведенных из СО K', движущейся относительно системы K с известной скоростью v₀(t)?

Р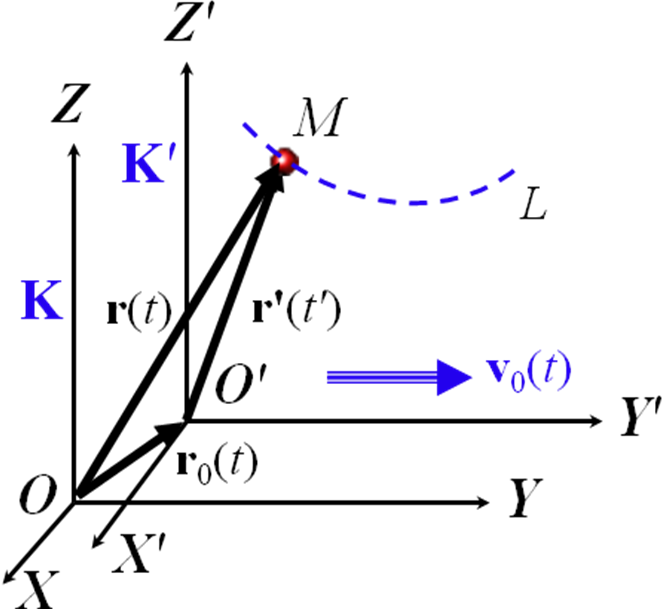 ассмотрим движение некоторой материальной точки из двух СО - K и K'

Радиус-вектор, соединяющий начала этих СО (точки O и O'), обозначим r_o(t)

р адиус-вектора частицы относительно выбранных СО обозначим r(t) и r'(t')

Очевидно

По определению, скорость – производная радиус вектора по времени

Таким образом видим, что для однозначного определения кинематических параметров, описывающих движение материальной точки относительно СО K, по измерениям, проведенным в СО K', необходимо знать связь моментов времени t и t₀

В классической механике проблема взаимосвязи моментов времени в различных СО решается постулатом Галилея

М оменты времени в различных СО совпадают с точностью до постоянной величины, определяемой процедурой синхронизации часов

О бычно считают часы синхронизированными таким образом, что const = 0, то есть

При таком способе синхронизации из последнего уравнения несложно получить связь ускорений в произвольных СО, где a_o - ускорение системы K₀ относительно системы K

Эти уравнения называют преобразованиями Галилея для произвольных СО

С реди всех возможных СО особое место занимает множество таких СО, которые относительно друг друга движутся с постоянными скоростями (т.е. их относительные ускорения равны нулю)

Такие СО называют инерциальными системами отсчета (ИСО)

Н айдем преобразования Галилея для ИСО. Положение начала ИСО K₀ можно найти, как уравнение движения, восстановленное по известной скорости v_o=const , где r₀(t₀) - радиус-вектор начала ИСО K' (т.е. точки O') в начальный момент времени t₀

Тогда, принимая t₀= 0 и r₀(t₀) = 0, получим преобразования Галилея для ИСО

О братим особо внимание на последнее уравнение в преобразованиях Галилея для ИСО, которое означает, что ускорение материальной точки во всех ИСО одинаково

9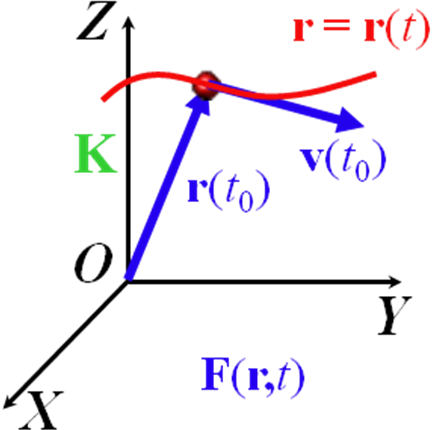 . Динамика материальной точки – 1 Закон Ньютона

1 Закон Ньютона

СО, в которых закон движения однозначно определен, если заданы:- начальные условия r₀=r(t₀), v₀=v(t₀) - функция, описывающая взаимодействие с окружающей средой F(r,t) называют ИСО

Задача законов Ньютона – выяснить причины движения

ИСО существуют, как математическая абстракция реальных систем отсчета

10. Динамика материальной точки – 2 Закон Ньютона

Сравним способы получения уравнений движения

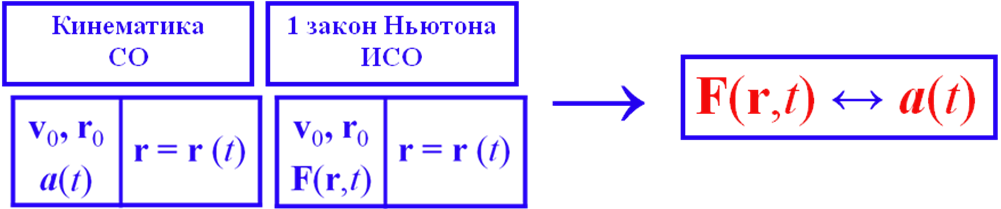
Ф ормулировка 2 закона Ньютона: в ИСО взаимодействие объекта с окружающей средой вызывает ускорение объекта , где m - инертная масса тела, F(t) - сила

в ИСО сила вызывает ускорение объекта

11. 3 Закон Ньютона

3 Закон Ньютона в общем случае является универсальным законом взаимодействий

Всякое действие вызывает равное по величине противодействие

Формулировка 3 закона Ньютона: При любом физическом взаимодействии, действие одного тела на другое вызывает равное по величине и противоположно направленное действие второго тела на первое

силы, связанные по 3 закону Ньютона, приложены к различным телам