Физическая реальность и её моделирование.
Материальная точка – физическое тело, размерами которого можно пренебречь по сравнению с расстояниями до тех объектов, с которыми изучаемое тело находится во взаимодействии.
Материальная точка – это математическая абстракция реального тела природы.
М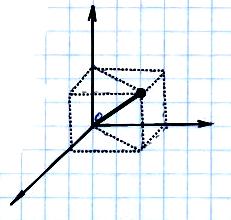
атериальной
точкой будем
называть любую точку пространства,
которой приписаны все физические
параметры данного тела.
Система координат – правило, по которому каждой точке пространства можно поставить в соответствие n чисел, называемых координатами точки. Минимальное количество координат, необходимое для описания положения точки в пространстве, называют размерностью пространства
Простейший пример системы координат – Декартова система координат
Системой отчёта будем назвать совокупность базиса и градуировки.
Базис – множество физических лабораторий (реальных или воображаемых), расположенных во всех точках пространства и снабжённых приборами для измерения времени и отрезков длины.
Г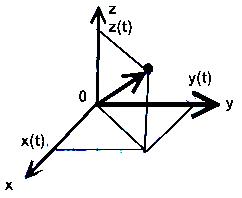
радуировкой
будем называть
правило, по которому каждому событию в
физическом пространстве можно поставить
в соответствие 4 числа, 3 из которых
определяют координаты этого события в
пространстве (то есть задают систему
координат), а 4-ое – момент времени, в
который это событие произошло.
В соответствие данному определению, систему отчёта обычно изображают как систему координат с дополнительным обозначением, указывающим на возможность измерения времени (обычно - K).
Рассмотрим
движение материальной точки относительно
некоторой СОK.
Пусть за некоторый промежуток времени
материальная точка переместилась из
точки пространства М1 в точку М2. Соединим
начало СК (совмещённой с выбранной СО)
с точками М1 и М2 – это радиус вектора
и
.
Уравнение движения, описывающее положение радиус-вектора (т.е. материальной точки) можно записать в векторном виде или в координатной форме
.
Оси должны быть расположены по правила буравчика = по правой тройке векторов.
К инематические и динамические характеристики движения точки
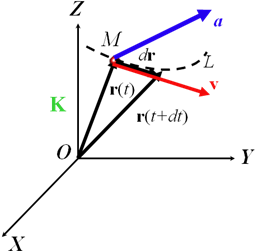
Рассмотрим элементарное (за время dt) перемещение материальной точки вдоль траектории L.
Элементарный отрезок dr, направленный вдоль движения материальной точки, называют вектором элементарного перемещения, а его длину |dr| –элементарным путем dS.
С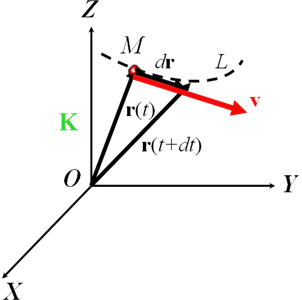
умма
элементов путей вдоль траектории даст,
очевидно, длину траектории, то есть
путь:
,
где S
– путь, пройденный материальной точкой.
Определение представляет путь, как сумму модулей (т.е. положительных величин) и, следовательно, путь может только возрастать
Производную радиус-вектора по времени называют вектором скорости материальной точки. Вектор скорости (как и dr) направлен по касательной к траектории. Величина скорости есть модуль (длина) вектора скорости.
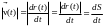
Таким образом, величина скорости есть производная пути по времени
- показывает быстроту возрастания пути, пройденного материальной точкой, со временем
Производную вектора скорости по времени называют вектором ускорения материальной точки.
Ускорение
Аналогично скорости, ускорение измеряет быстроту изменения вектора скорости при движении материальной точки в пространстве.