Тема. Производная. Правила дифференцирования. Таблица производных.

Цель. Рассмотреть и изучить следующие вопросы:

1. Основные правила дифференцирования: производная произведения и частного. Частные случаи.

2. Производная тригонометрических функций.

3. Производные логарифмической, показательной и степенной функции.

4. Производная обратной функции. Производные обратных тригонометрических функций.

5. Производная сложной функции.

6. Таблица производных основных элементарных функций.

Литература: [1] гл.3 §§ 4 – 7; 9;11; §§ 8, 12-15

Математика приводит нас к дверям истины,

но самих дверей не открывает.

В.Ф. Одоевский

Опорные знания.

Приращение аргумента (приращением независимой переменной) в фиксированной точке называется значение выражения

Приращением функции в фиксированной точке называется значение выражения

Замечания.

1) При фиксированном значении приращение является функцией от .

2) Для корректного определения необходимо, чтобы и принадлежали .

3) Приращение называют также приращением зависимой переменной и для функции обозначают .

Секущая к графику функции называется прямая, проходящая через любые две точки данного графика функции.

Е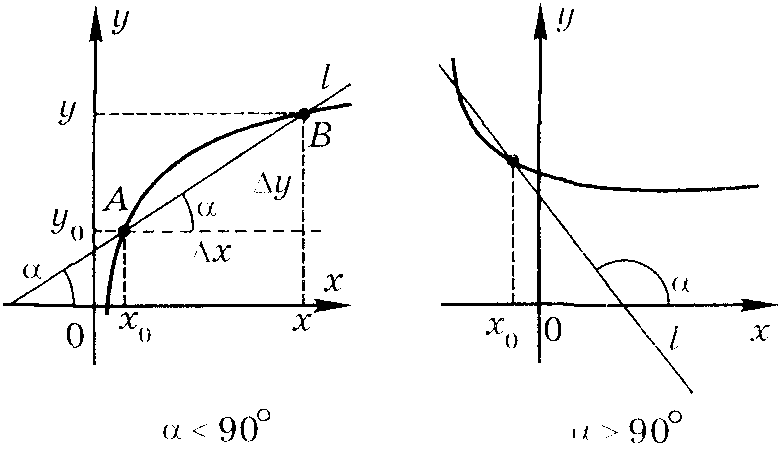 сли уравнение секущей к графику функции, проходящей через точку , задано формулой , то , где - угол, который образует секущая с положительной полуосью оси абсцисс.

Функция стремится к числу при , стремящемся к , если в окрестности точки разность может быть сколь угодно мала. Это означает, что для любого числа найдется число , такое, что если , то .

При этом число называется пределом функции в точке .

Обозначение. или при .

Замечание. Исходя из определения приращения аргумента, условие равносильно условию .

Производная функции.

Производной функции в точке называется число, к которому стремится разностное отношение при .

Обозначение. Производная функции в точке обозначается . Таким образом,

.

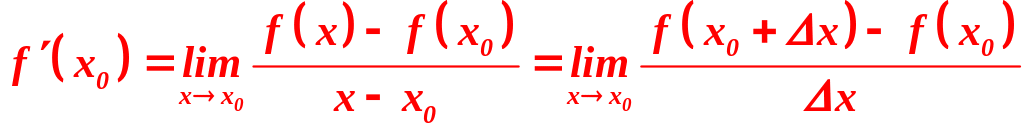Иными словами, производной функции в данной точке называется отношение приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Функция называется дифференцируемой в точке , если она имеет производную в этой точке.

Функция , сопоставляющая каждому значению из множества точек, в которых дифференцируема, значение , называется производной функции .

Нахождение производной данной функции называется дифференцированием функции .

Вычисление производных по определению

Правило 1. Производная произведения

Если то .

Доказательство.

Пусть , дадаим приращения: ,

Найдём ,

Найдём отношение :

Найдём предел отношения :

,

,

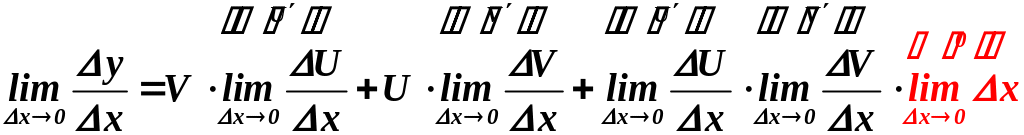Правило 2. Производная частного .

Доказательство.

где и – дифференцируемые функции и

или ,

,

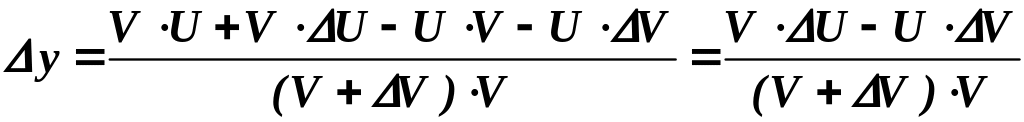Пусть . Так как функция – дифференцируема, то она непрерывна и следовательно, поэтому

,

получим

.

Частный случай: .

Правило 3. Постоянный множитель можно выносить из под знака производной.

Пусть .

.

Частный случай: .

Производная от функции

Пусть .

Имеем:

Найдём отношение :

или .

Переходя к пределу при и пользуясь теоремой о пределе произведения имеем ,

.

Вывод: .

Производная от функции