10. Основные теоремы о пределах

Теорема 1: Предел алгебраической суммы конечного числа функций, каждая из которой имеет конечный предел, равный алгебраической сумме пределов этих функций, т.е. .

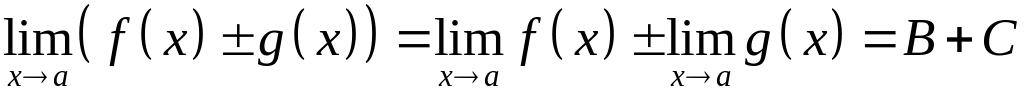Теорема 2: Предел произведения конечного числа функций, каждая из которых имеет конечный предел, равен произведению пределов этих функций, т.е. .

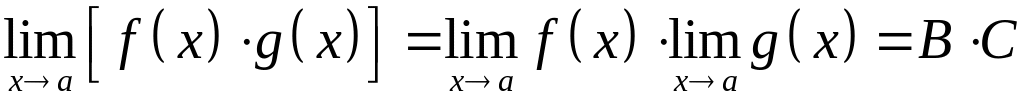Доказательство.

По теореме о связи предела с бесконечно малой: , где - бесконечно малые.

Перемножим почленно .

Положим, - бесконечно малая ( ), т.е. .

Тогда по той же теореме о связи: . Теорема доказана.

Теорема 3: Предел частного двух функций, каждое из которых имеет конечный предел, равный частному пределов этих функций, при условии, что предел знаменателя не равен нулю, т.е. .

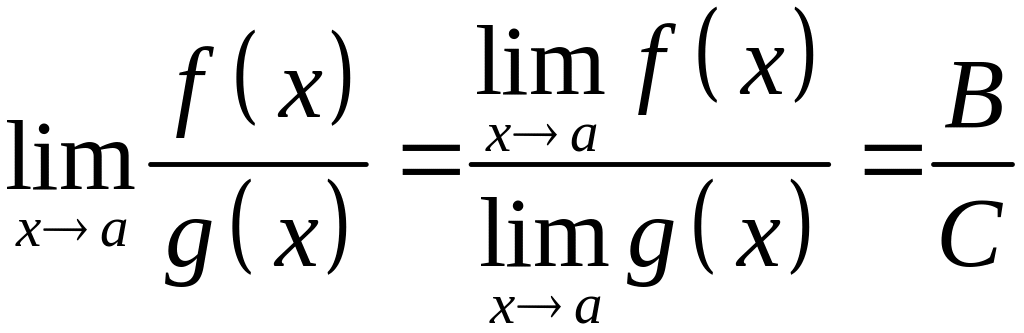Вычисление пределов (некоторые случаи)

Чтобы найти предел, нужно подставить значение а к которому стремится х в функцию и далее будем иметь следующие случаи:

1. Непосредственная подстановка приведет к вычислению предела:

2. .

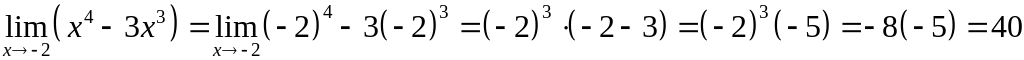
а) если многочлен, то раскладывается на множители и сокращается.

б) если иррациональные выражения, то домножают и делят на сопряженное выражение.

в) если бесконечно малое, то используют эквивалентность бесконечно малых. .

а) если многочлен, то надо делить его на старшую степень.

.

б) , если степень числителя больше степени знаменателя,

в) =0, если степень числителя меньше степени знаменателя.

3. . Сводят к неопределенностям вида .

4. . Свести к , путем преобразования функции к дроби.

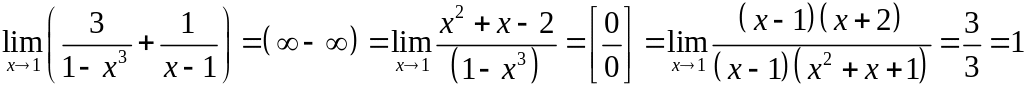
11. Первый и второй замечательный пределы

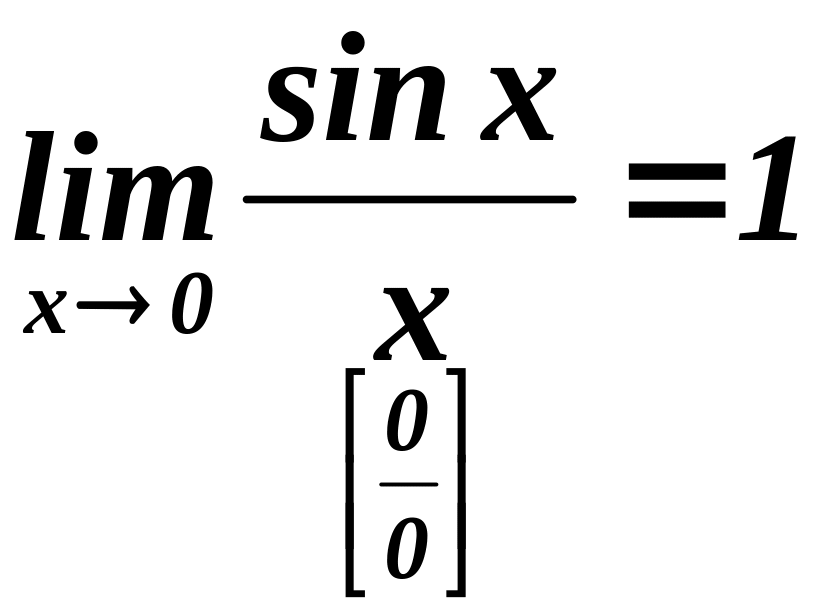- первый замечательный предел.

Применение: .

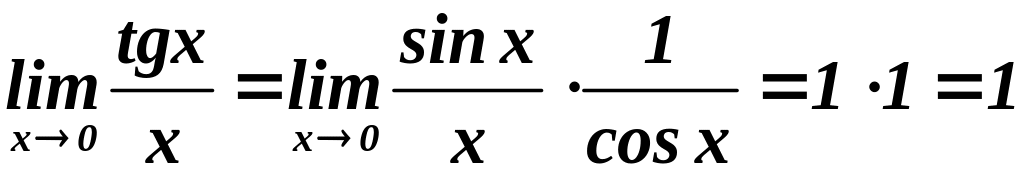- второй замечательный предел.

Применение: .

12. Непрерывные функции

Определение. Функция называется непрерывной в точке а, если 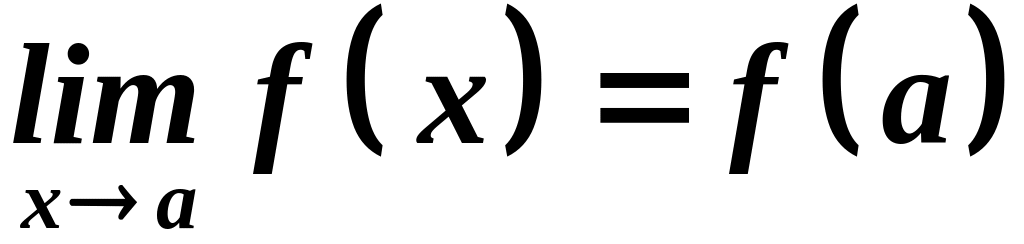, т.е. .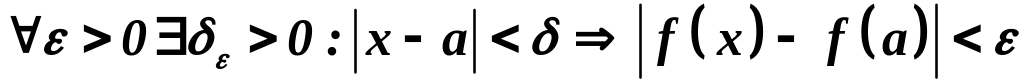

Определение. Функция называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.

Определение. Точка а называется точкой разрыва функции , если в этой точке функция не является непрерывной.

Различают точки разрыва I и II – го рода.

Определение. Точка разрыва, а функции называется точкой разрыва I-го рода, если в этой точке существуют и конечны оба односторонних предела.

- точка скачка. Скачек, равен: .

- точка устранимого разрыва I рода.

Определение. Точка разрыва а - называется точкой разрыва II-го рода, если в этой точке, по крайней мере, не один из односторонних пределов или равен .

Применение.

1) 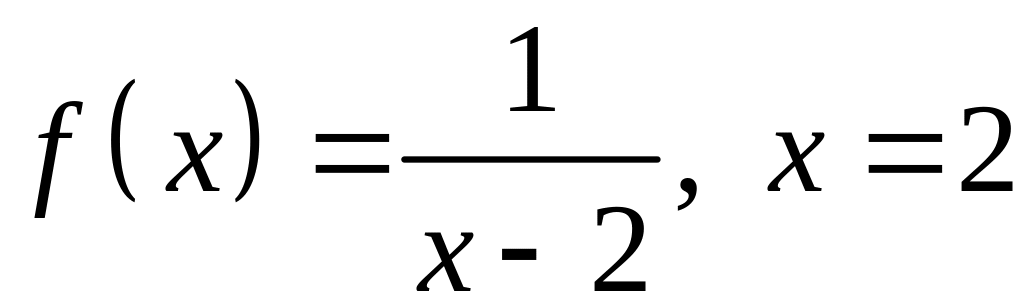- точка разрыва.

, ,

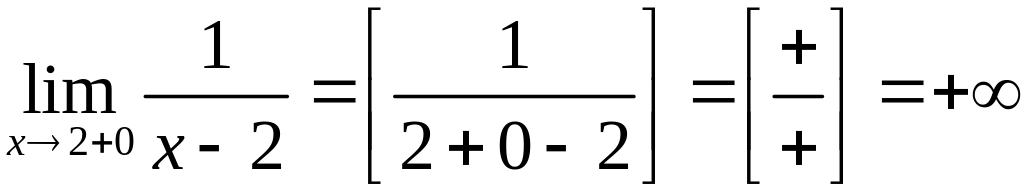- II-го рода (т.е. вертикальная асимптота графика):

2) .

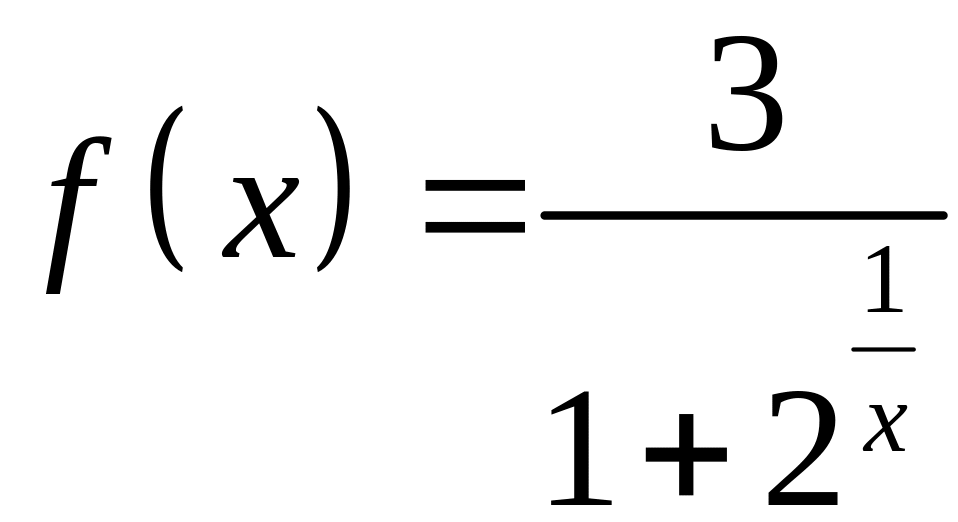Функци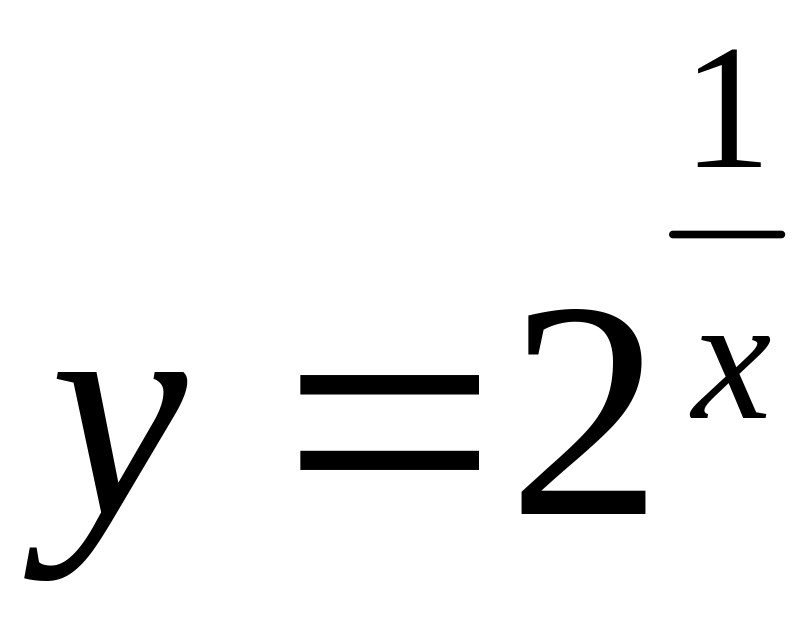я - показательная, неотрицательная, следовательно, знаменатель никогда в 0 не обратится. Функция 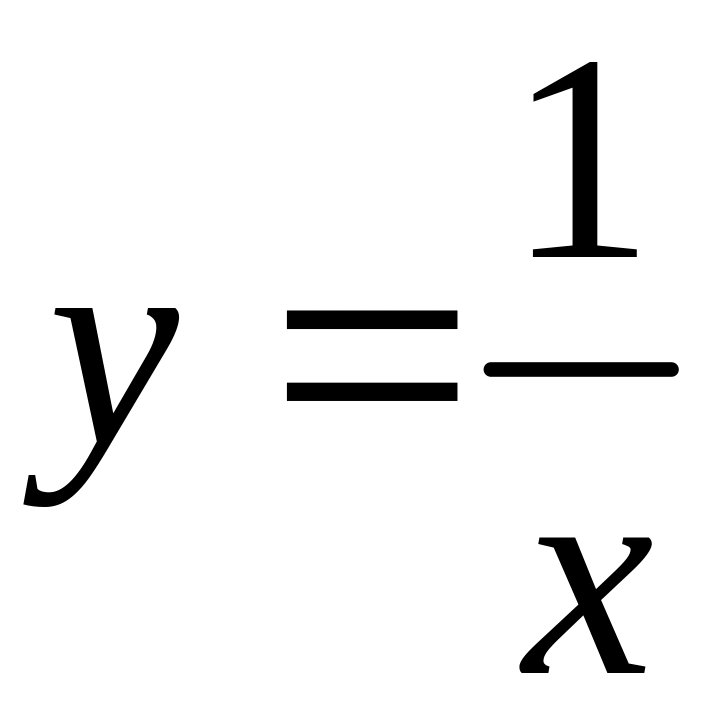- непрерывная функция, кроме нуля.

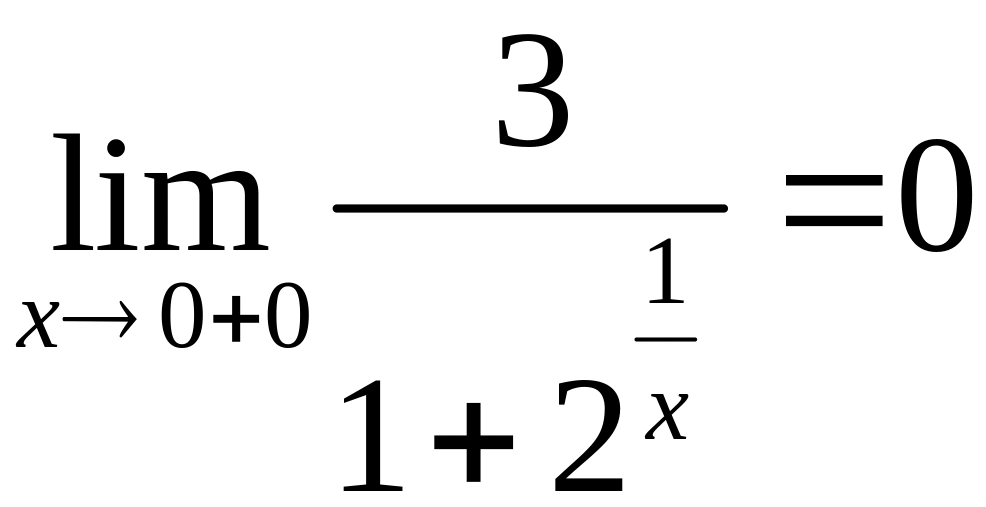
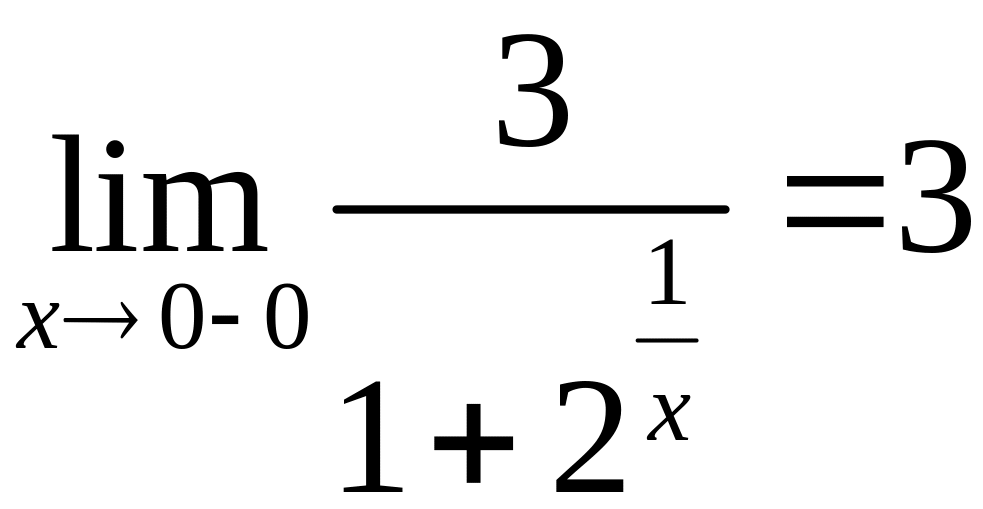; . Скачек, равен . Точка разрыва I-го рода.

13. Свойства функции, непрерывной на отрезке.

Теорема 1. (1 теорема Вейерштрасса).

Если функция непрерывна на отрезке , то она ограничена на этом отрезке.

Определение. Число М называется наибольшим значением функции на множестве Х, если для всех выполняется неравенство , причем, во множестве Х существует, по крайней мере, одна точка .

Определение. Число т называется наименьшим значением функции на множестве Х, если выполняется неравенство , причем во множестве X существует, по крайней мере, одна точка .

Теорема 2. (2 теорема Вейерштрасса). Если функция непрерывна на , то она принимает на этом отрезке свои наибольшие и наименьшие значения.

Теорема 3. (1 теорема Коши). Если функция - непрерывна на отрезке и на концах этого отрезка принимает значения, разных знаков, то на отрезке найдется, по крайней мере, одна точка .

Г еометрический смысл. График функции на по крайней мере 1 раз пересекает Ох.

Теорема 4. (2 теорема Коши). Если непрерывна на отрезке , то она принимает на этом отрезке все свои промежуточные значения.

Пояснения: По теореме 2 принимает свои и на . Рассмотрим отрезок . Теорема 4 утверждает, что каково бы не было число С: на найдется точка С: .