8. Период заданной функции.
Определение
18.
Функция
называется периодичной,
если существует такое число
,
что выполняется
два условия:
1.
для
любого
;
2.
выполняется равенство:
.
8.2. Для нахождения периода функции необходимо:
1.
Выделить
основной период функции (для
он равен
);
2.
Приравнять
коэффициент
,
стоящий перед переменной
в аргументе функции,
:
для
,
получим
;
3.
Выразить
из данного равенства период
.
Примеры.
А)
;
Б)
;
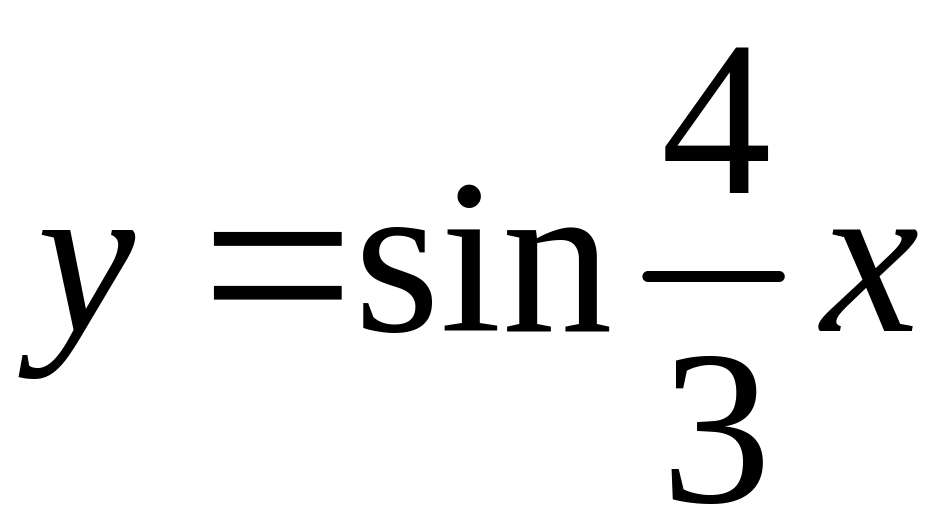С)
.
9. Основные элементарные функции.
Определение
19. Тригонометрические и обратные
тригонометрические функции, степенная
,
показательная (
,
),
логарифмическая (
,
),
функции называются основными элементарными
функциями.
Функция |
|
|
Ограничен-ность |
Четно-сть |
Нечет-ность |
Перио-дич- ность |
|
|
|
нет |
нет |
нет |
нет |
|
|
|
нет |
нет |
нет |
нет |
|
|
|
нет |
нет |
нет |
нет |
|
|
|
да |
нет |
да |
да
|
|
|
|
да |
да |
нет |
да
|
|
|
|
нет |
нет |
да |
да
|
|
|
|
нет |
нет |
да |
да
|
|
|
|
да |
нет |
да |
нет |
|
|
|
да |
нет |
нет |
нет |
|
|
|
да |
нет |
да |
нет |
|
|
|
да |
нет |
нет |
нет |
,
,
Определение 20. Функции, которые получаются посредством конечного числа арифметических операций и конечного числа суперпозиций из основных элементарных функций, называются элементарными.
2. Числовая последовательность и ее предел
Выпишем все натуральные числа и к каждому поставим в соответствие действительное число:
п |
1 |
2 |
… |
п |
… |
х |
|
|
… |
|
… |
Определение.
Если
каждому натуральному числу п
поставить в соответствие единственное
число
,
то говорят, что множество этих
действительных чисел образуют числовую
последовательность
.
Пример.
-1 |
1 |
-1 |
1 |
… |
|
1 |
|
|
|
… |
|
Числа
называют ее членами,
-
п-ый
член последовательности. Ясно, что роль
множества Х
в определении играет множество натуральных
чисел N,
поэтому числовая
последовательность
есть
функция натурального аргумента
.
Пусть дана числовая . Может оказаться так, что с возрастанием номера п члены последовательности всё ближе и ближе подходят к действительному числу В. В этом случае В есть предел данной числовой .
Возьмем
сколь угодно малое число
т.к. все члены последовательности с
возрастанием
все ближе и ближе подходят к числу В,
то расстояние между В
и членом последовательности
будет неограниченно уменьшаться и может
стать меньше задуманного числа
т.е.
некоторого п.
Дадим строгое определение.
Определение.
Число В
называется пределом
если
. (1)
Этот
факт символически записывается так:
.