11. Непрерывные случайные величины. Функция распределения и плотность распределения вероятностей

Наряду с дискретными случайными величинами, принимающими конечное или счетное множество значений в теории вероятностей широко используются непрерывные случайные величины. Множество непрерывной случайной величины несчетно и обычно представляет собой некоторый промежуток.

Определение. Случайная величина Х называется непрерывной, если существует неотрицательная функция такая, что для каждого х функцию распределения непрерывной случайной величины Х можно представить в виде

.

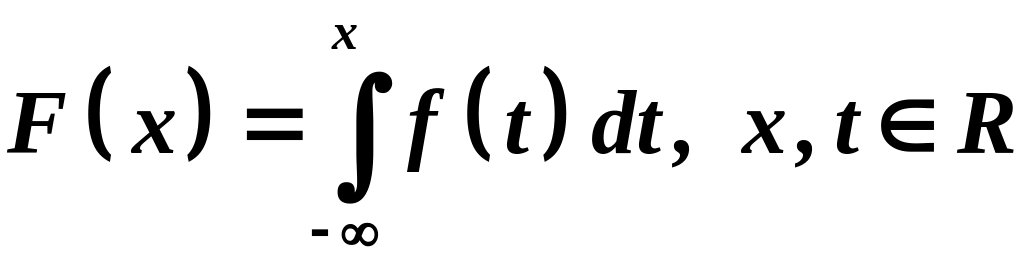Свойства функции распределения непрерывной случайной величины

1. т.е. ;

2. есть непрерывная, неубывающая функция;

3. .

Определение. Плотностью распределения непрерывной случайной величины называется первая производная от функции распределения:

.

Свойства плотности

1. Плотность распределения неотрицательна, т.е. .

2. Несобственный интеграл от плотности распределения по всей числовой прямой равен единице: .

Непрерывная случайная величина считается заданной, если задана ее функция распределения или плотность распределения вероятностей. При этом функция распределения называется интегральным законом, а плотность распределения – дифференциальным законом распределения.

Вероятность того, что случайная величина Х примет значения из интервала находится по формуле:

.

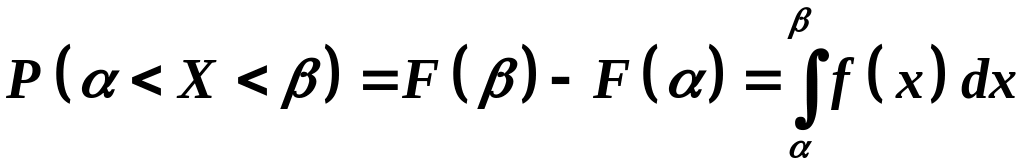Примечание. Интервал для возможных значений непрерывной случайной величины Х может быть и замкнутым, т.е.

.

Пример 1. Дана функция распределения непрерывной случайной величины Х:

.

Найти плотность распределения непрерывной случайной величины Х и построить графики функции распределения и плотности распределения. Определить вероятность того, что Х попадет в интервал .

Решение. Плотность распределения равна первой производной от функции распределения:

.

Графики функции распределения и плотности распределения представлены на рисунках 4 и 5.

Рис. 4 Рис. 5

Вероятность того, что Х попадает в интервал , найдем по формуле:

.

Пример 2. Задана плотность распределения непрерывной случайной величины Х:

.

Найти коэффициент А, функцию распределения непрерывной случайной величины и вероятность того, что Х примет значение, принадлежащее интервалу .

Решение. Для нахождения константы А воспользуемся свойством плотности .

Тогда для заданной непрерывной случайной величины Х:

.

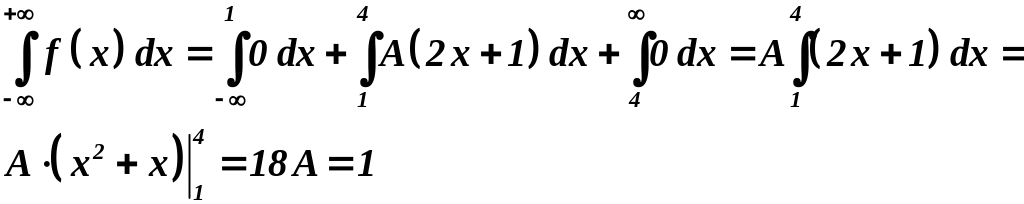Получаем 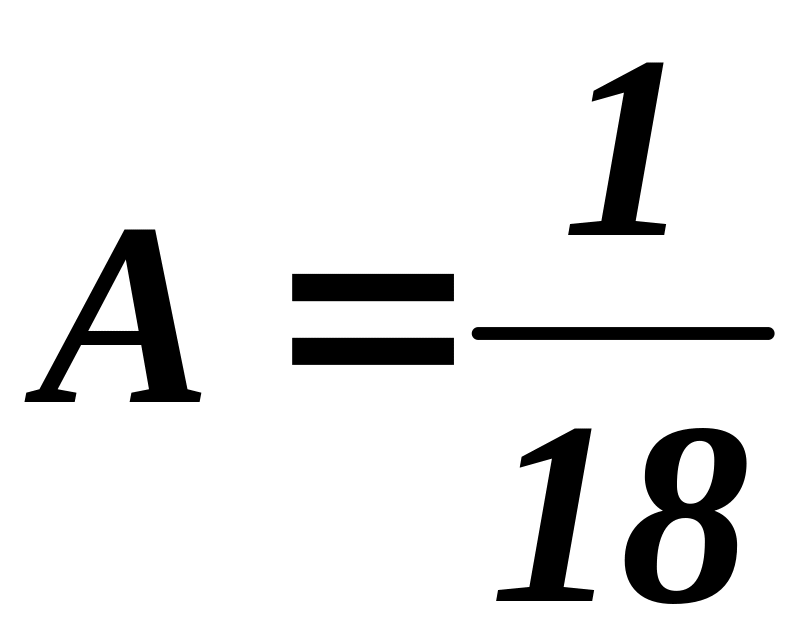, а плотность распределения имеет вид:

.

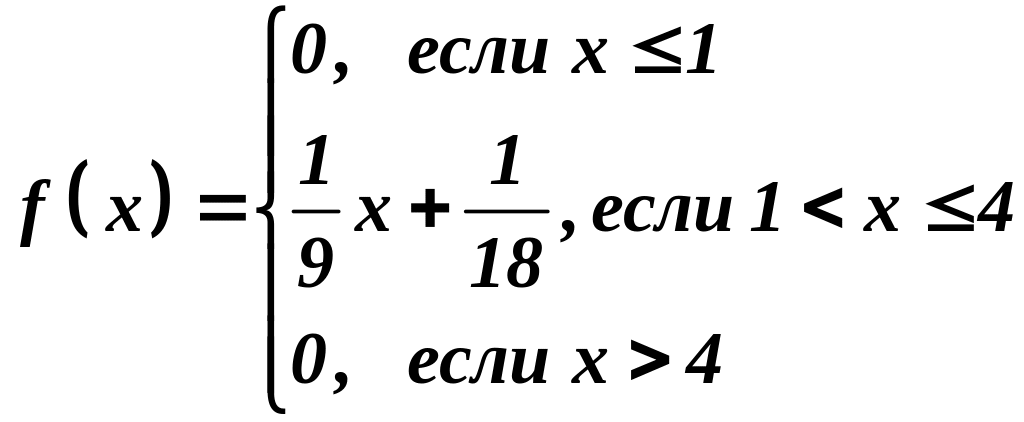Для отыскания функции распределения воспользуемся формулой:

.

Если , то , следовательно .

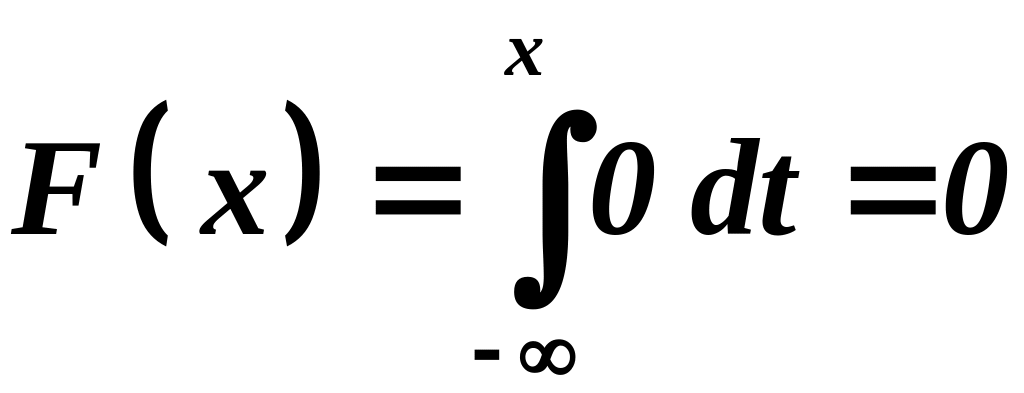Если , то и

.

Если , то и

.

Итак, искомая функция распределения:

.

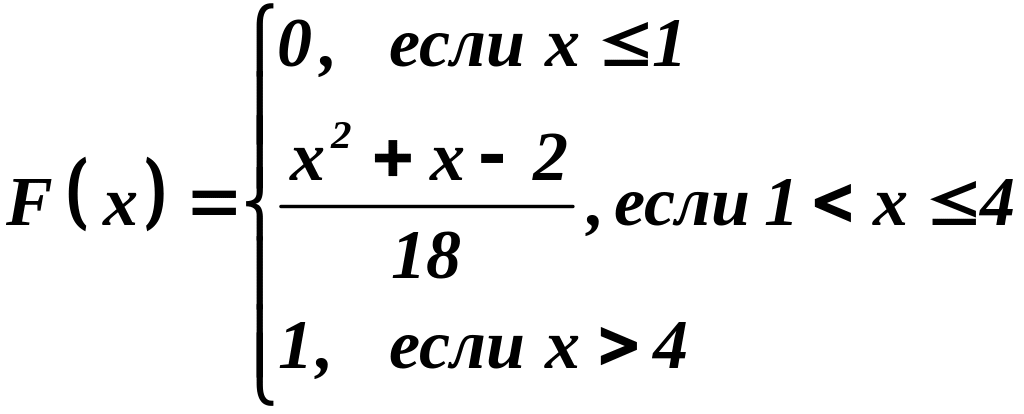Вероятность того, что Х примет значение, принадлежащее интервалу , найдем по формуле:

Среди непрерывных случайных величин наиболее распространены случайные величины, подчиняющиеся нормальному, равномерному и показательному законам.

12. Числовые характеристики непрерывной случайной величины

Определение. Математическим ожиданием непрерывной случайной величины Х называют среднее значение Х, которое определяется равенством ,

где плотность распределения непрерывной случайной величины Х.

В частности, если все возможные значения принадлежат интервалу , то .

Все свойства математического ожидания, указанные для дискретной случайной величины, сохраняются и для непрерывных случайных величин.

Определение. Дисперсией непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох определяются равенством ,

или равносильным равенством:

.

В частности, если все возможные значения , то

.

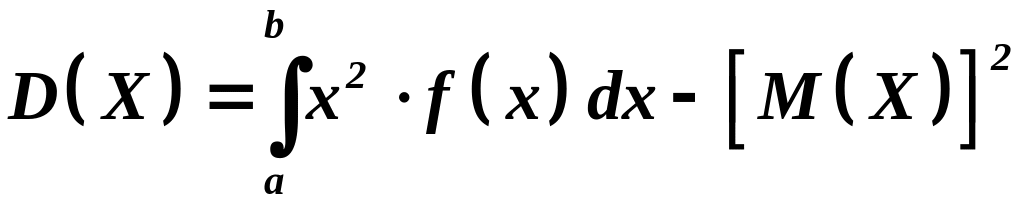Все свойства дисперсии, указанные для дискретной случайной величины сохраняются и для непрерывной случайной величины

Определение. Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной случайной величины .

Определение. Модой для непрерывных случайных величин Х называется точка максимума плотности распределения. Мода может быть не единственной.

Определение. Медианой случайной величины Х называется то ее значение, для которого .

У дискретной случайной величины может не существовать медианы.

Кроме характеристик положения – средних типичных значений случайной величины – употребляется еще ряд характеристик: например, так называемые моменты.