4. Вероятность появления хотя бы одного события

В некоторых случаях вероятность события удобнее подсчитывать как вероятность противоположного другому событию.

Пусть события независимы и известны вероятности этих событий:

.

Обозначив вероятности противоположных событий

,

найдем вероятность того, что ни одно из событий в опыте не наступит:

.

В этом случае искомая вероятность, т.е. вероятность появления хотя бы одного события определяется как вероятность противоположного события: .

Пример. Производится 2 выстрела по мишени. Вероятности попаданий при этом равны 0,5 и 0,6. Найти вероятности того, что в мишени будет: а) ровно одна пробоина; б) хотя бы одна пробоина.

Решение. Обозначим события: А – ровно одна пробоина; В – хотя бы одна пробоина; попадание при I выстреле; попадание при II выстреле.

а) если ровно одна пробоина, то , причем слагаемые несовместны, а сомножители независимы.

Для вероятности:

б) В – хотя бы одна пробоина, ни одной пробоины. .

.

Ответ: 0,8.

5. Формула полной вероятности

Следствием основных теорем сложения и умножения вероятностей является так называемая формула полной вероятности.

Теорема. Пусть некоторое событие А может произойти вместе с одним из событий , образующих полную группу несовместных событий, называемых гипотезами ( независимые и ). Тогда вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе, т.е.

.

Доказательство. Т.к. гипотезы образуют полную группу, то событие А может появиться только в комбинации с какой-либо из этих гипотез: .

Так как гипотезы несовместны, то и их комбинации несовместны. Применим к ним теорему сложения вероятностей: .

Применяя к событию теорему умножения, получим:

.

Тогда

.

Теорема доказана.

Пример. Продукция 3 фабрик ювелирных изделий поступает на продажу в магазин. Вероятность брака на 1 фабрике равна 0,2, а на второй и третьей фабрике 0,1. Какова вероятность покупки одного небракованного изделия в магазине, если 30% всей продукции в магазине изготавливается на 1 фабрике, 50% - на второй и 20% - на третьей фабриках?

Решение. Обозначим события: А – купленное изделие не имеет брака. Выдвигаем гипотезы: купленное изделие изготовлено на первой фабрике; купленное изделие изготовлено на второй фабрике; купленное изделие изготовлено на третьей фабрике: образуют полную группу событий: .

После наступления одного из событий или , т.е. куплено изделие одной из фабрик, определяем, браковано оно или нет.

Условная вероятность события А – изделие не имеет брака при гипотезах и соответственно равны: (т.к. вероятность брака на I фабрике равна 0,2, а это событие противоположно тому, что изделие 1 фабрики не бракованное);

; .

Тогда по формуле полной вероятности:

.

6. Формула Бейеса

Следствием теоремы умножения и формулы полной вероятности является так называемая теорема гипотез или формула Бейеса.

Поставим следующую задачу.

Пусть имеется полная группа несовместных событий . Вероятности этих гипотез до опыта известны и равны соответственно . Произведен опыт, в результате которого наблюдалось появление события А. Спрашивается, как следует переоценить вероятности гипотез в связи с появлением этого события?

Теорема. Условная вероятность для каждой гипотезы при условии, что событие А произошло, равно отношению произведения вероятности гипотезы до наступления события А и условной вероятности А при наступлении к полной вероятности события А, т.е.

.

(доказательство после примера)

Пример. Два стрелка независимо друг от друга стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8, для второго – 0,4. После стрельбы в мишени обнаружена 1 пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку.

Решение. До опыта возможна следующие гипотезы: ни первый, ни второй стрелок не попадет; оба стрелка попадут; первый попадет, второй промахнется; первый промахнется, второй попадет.

Вероятности этих гипотез:

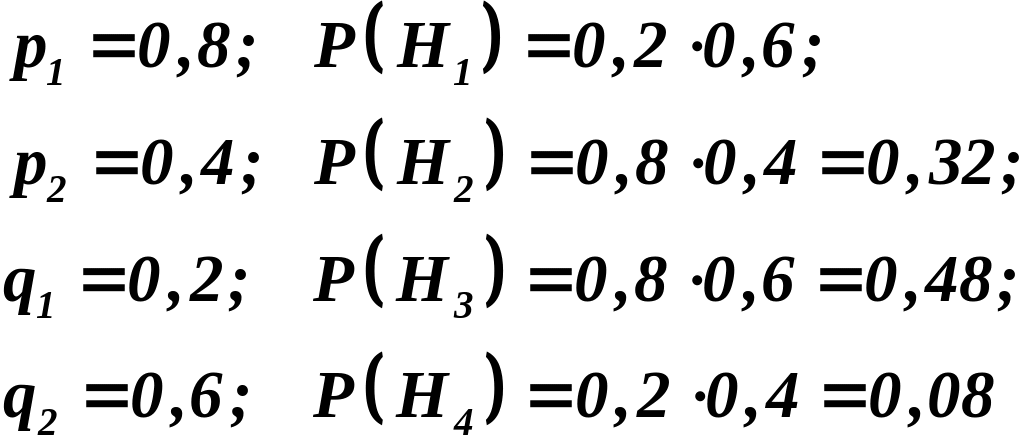
(Проверка: )

Значит, образуют полную группу несовместных событий.

Условные вероятности события А – «в мишени одна пробоина», при этих гипотезах равны:

; ; ; .

После наступления события А переоценим условные вероятности гипотез при условии, что А произошло. По формуле Бейеса:

Следовательно, вероятность того, что пробоина принадлежит первому стрелку, равна .

Доказательство теоремы. находим из условия

. Получим . Теорема доказана.