6.2. Решение транспортной задачи

Транспортная задача является классическим примером задачи оптимизации, решаемой с помощью инструментария Excel Поиск решения.

Ее формулировка состоит в следующем: имеется несколько пунктов производства и пунктов потребления некоторого продукта. Для каждого из пунктов производства задан объем производства, а для каждого пункта потребления – объем потребления. Известна также стоимость перевозки единицы продукта из каждого пункта производства в каждый пункт потребления. Необходимо составить план перевозок продукта, в котором все пункты потребления были бы обеспечены необходимыми продуктами, ни из какого пункта производства не вывозилось бы продуктов больше, чем там производится, а стоимость перевозки была бы минимальной.

Рассмотрим решение транспортной задачи на следующем примере.

Пример. Имеются производители продукции в городах: Курске, Орле, Калуге и Воронеже, которые выпускают товар соответственно в объеме a_i (I=1, ..,4). Продукция доставляется на склады или предприятия в г. Москве, Смоленске, Кирове, Твери, причем потребности каждого потребителя равны b_j (j=1,..,4). Требуется минимизировать затраты на перевозку товаров от предприятий- производителей на торговые склады. При этом необходимо учесть возможности поставок каждого из производителей при максимальном удовлетворении запросов потребителей.

6.2.1. Подготовка исходных данных

Для решения данной задачи надо построить ее математическую модель. Неизвестными здесь являются объемы перевозок. Пусть X_ij – объем перевозок с I- го завода на j=й склад. Функцией цели являются суммарные транспортные расходы:

,

где с_ij – стоимость перевозки единицы продукции и i-го завода на j-й склад. Следовательно, минимизировать надо функцию при следующих ограничениях:

где: a_i –объем производства на i-ом заводе, b_j – спрос на продукцию на j-ом складе.

Так как задача решается итерационным методом, то начальный план перевозок можно задать, считая, что каждый производитель поставляет по одному товару на каждый склад. Следовательно, начальный план перевозок представляется матрицей Х:

6.2.2. Выполнение работы

Скопируйтее файл Транспортная задача из папки Рабочие файлы в свою папку и откройте. Откроется рабочий лист с таблицей.

Введите в ячейки диапазона D5:G8 числа, равные 1. (начальный план перевозок)

В ячейках диапазона С5:С8 и D10:G10 подсчитайте общее число перевозок, сделанных каждым производителем с помощью команды Автосумма ленты Главная.

В ячейки диапазона D12:G12 введите значения, отражающие возможности складов по приему продукции, например, 240, 180, 300, 190 т.

В ячейки диапазона С14:С17 введите возможности поставщиков продукции, например, 250, 210, 280, 311 т.

В ячейки диапазона D14:G17 введите транспортные издержки на перевозку единицы продукции от поставщика к потребителю (на склад) например, выраженные следующей матрицей С:

Примечание.

В отличие от начального плана данные по объемам поставок, мощностям складов и стоимости перевозок в процессе решения задачи не меняются.

В ячейку С19 следует ввести выражение для вычисления целевой функции

.

Для этого: выделите ячейку D19 и введите формулу =D5*D14+D6*D15+D7*D16+D8*D17 для вычисления стоимости текущих перевозок по Москве (J=1). Скопируйте формулу из ячейки D19 в интервал ячеек E19:G19. В ячейках появятся результаты вычисления стоимости перевозок для других городов (j=2 ,3,4). Выделите ячейку С19 и введите в нее выражение для вычисления стоимости всех текущих перевозок =СУММ(D19:G19). Конечный вид исходных данных для решения транспортной задачи представлен на рис.6.12.

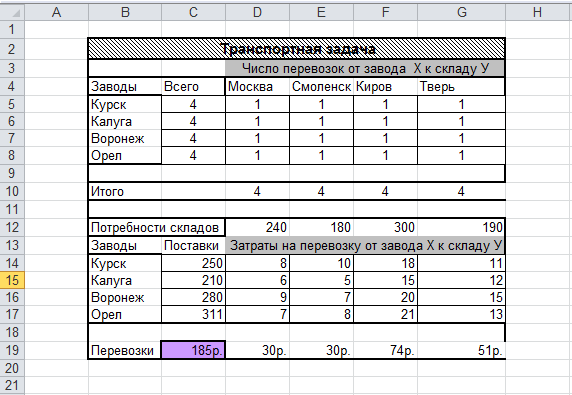
Рис.6.12. Подготовка данных для решения транспортной задачи