4. Нескінченно малі та нескінченно великі функції

Означення 1. Функція називається нескінченно малою при , якщо (можливо, що один із символів ).

Якщо функція є нескінченно малою при , будемо використовувати позначення ( ), яке читається “ дорівнює мале від 1 при ”.

Наприклад:

1) ; 2) ;

3) , ; 4) , ;

5) , .

Приклад 5. Величини , , є нескінченно малими при .

При нескінченно малими будуть функції , .

Функції , , 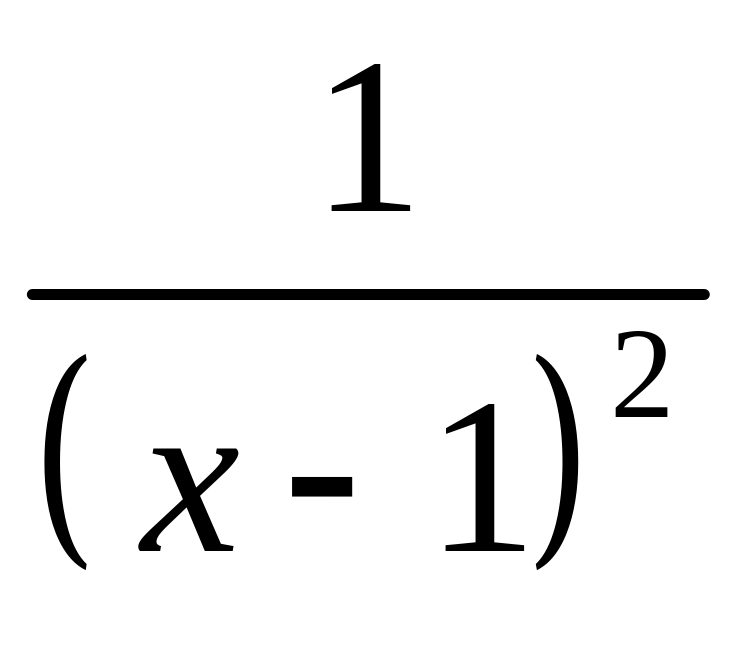, є нескінченно малими при .

Справедливі такі твердження:

1)

( )

( , чи будь-який з символів );

2) лінійна комбінація і добуток скінченного числа функцій, які є нескінченно малими при , є функцією, яка нескінченно мала при .

Означення 2. Функція називається нескінченно великою при , якщо .

Сума нескінченно великих функцій не завжди є нескінченно великою функцією .

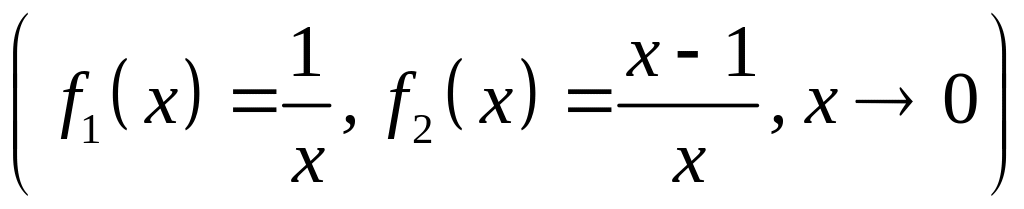Зв’язок між нескінченно малими і нескінченно великими величинами такий:

1) якщо є нескінченно малою при , то є нескінченно великою при ;

2) якщо є нескінченно великою при , то буде нескінченно

малою величиною при .

Приклад 6. Величини є нескінченно малими при . Зворотні величини , , будуть нескінченно великими при . При цьому тільки ( ), а величини та не прямують ні до , ні до (обміркуйте це, побудувавши графіки функцій).

Приклад 7. Функція є нескінченно великою при ; функція є нескінченно великою при ; функція є нескінченно великою при та при ; функція є нескінченно великою при .

Означення 3. Нехай функції та є нескінченно великими при . Якщо 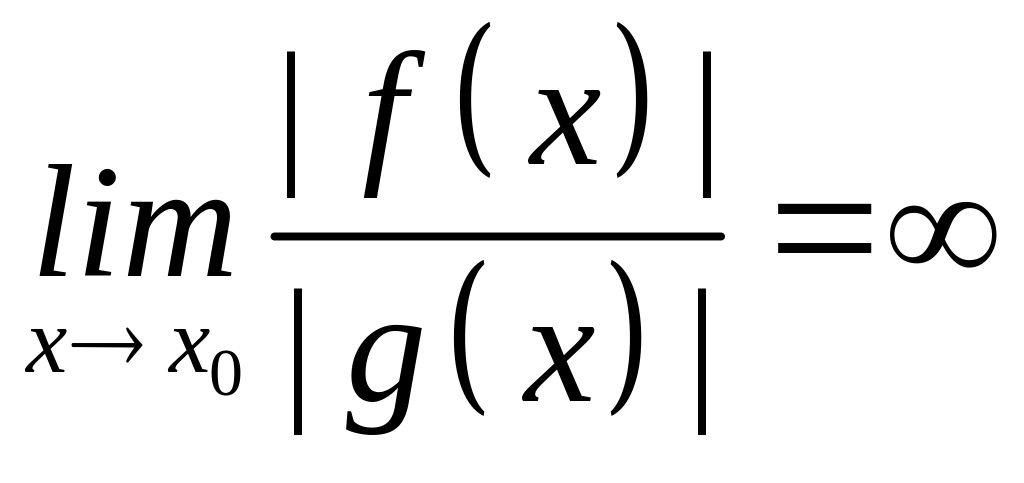, то будемо казати, що є нескінченно великою більш високого порядку, ніж ( зростає швидше, ніж ). Приклад 8. а) нескінченно велика більш високого порядку, ніж при

; б) більш високого порядку, ніж при .

Означення 4. Нескінченно малі (нескінченно великі) функції та називаються еквівалентними (асимптотично рівними) при , якщо .

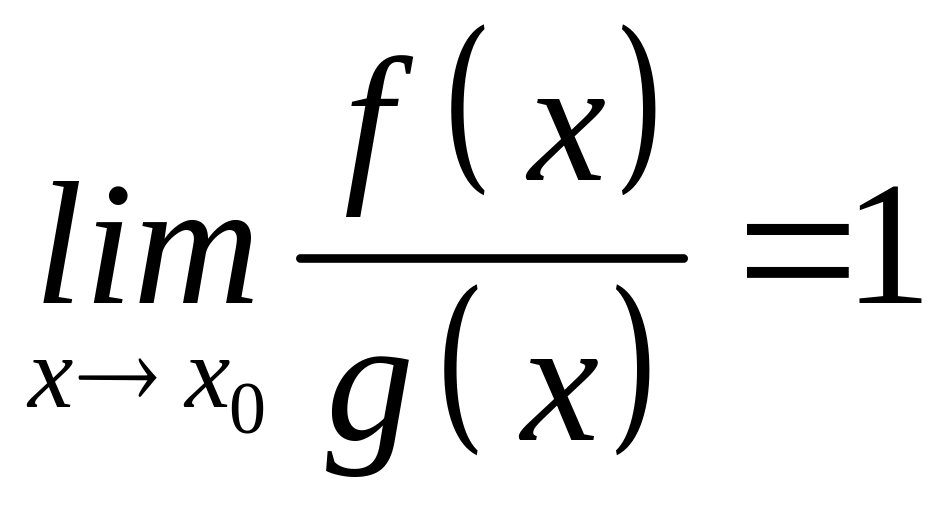Звичайно для еквівалентних функцій застосовують позначення

,

і говорять, що функції та асимптотично рівні в точці . Прийнято в асимптотичній рівності зліва писати громіздку функцію, яка вивчається, а справа – більш просту, яка вже вивчена до цього.

Приклад 9. Довести, що а) , ;

б) , , .

Розв’язання. а) ;

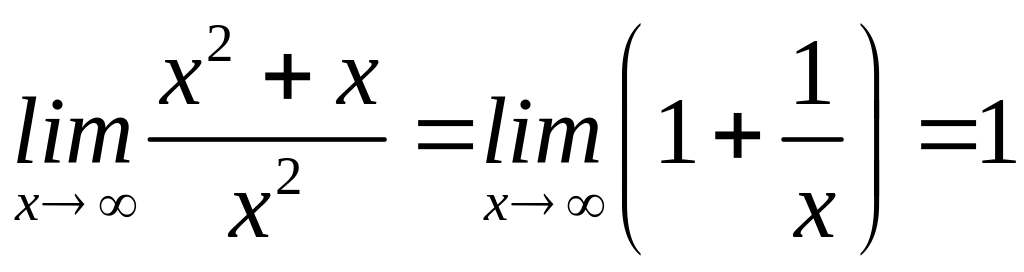б)

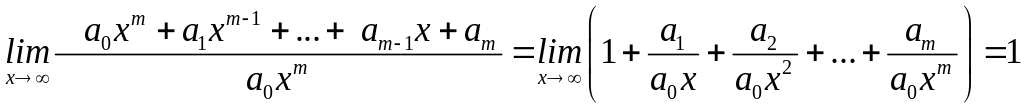
Таким чином, з прикладу 9б випливає наступне твердження.

Теорема 3. Сума нескінченно великих різних порядків еквівалентна нескінченно великій найбільш високого (старшого) порядку.

Асимптотичні формули можна почленно перемножати і ділити, а саме

1) , 2) ( при ).

Інакше кажучи, при обчисленні границь добуток, відношення початкових функцій та можна замінити добутком (відношенням) еквівалентних їм функцій та .

Приклад 10. Обчислити границі: а) ;

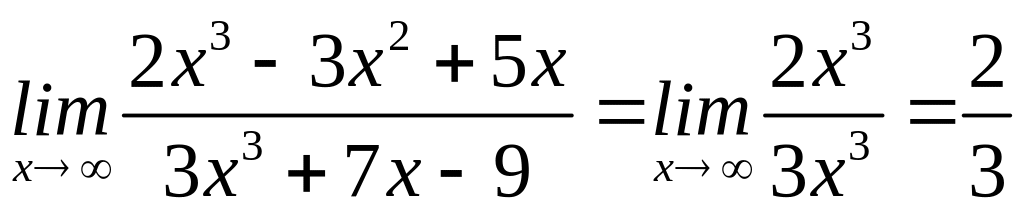б)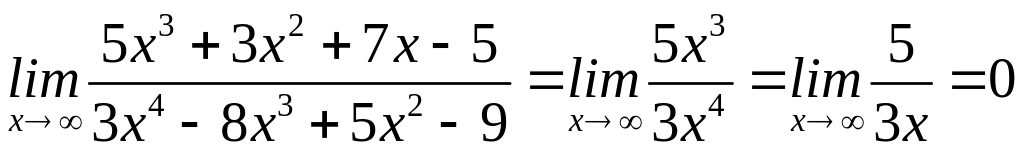 ; в)

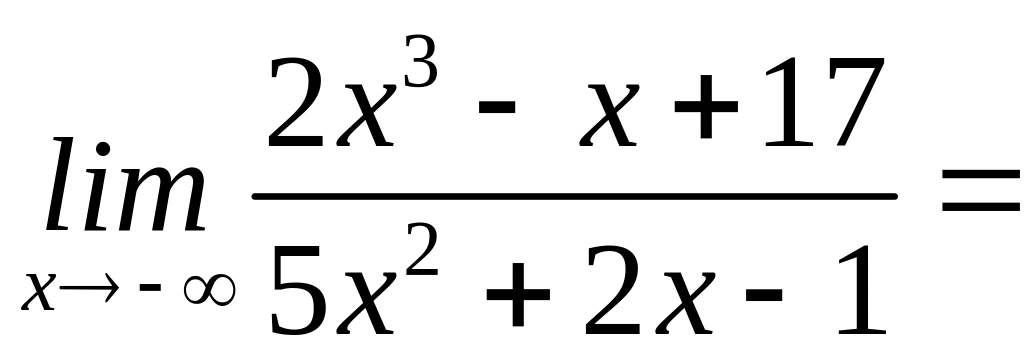
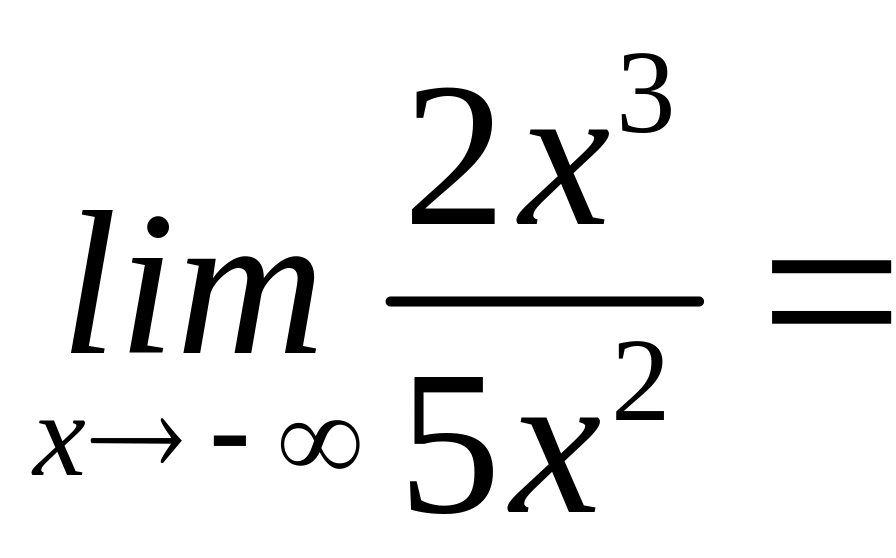
Перша важлива границя. Спробуємо з’ясувати, чи існує границя функції при . З цією метою обчислимо значення цієї парної функції при декількох достатньо малих значеннях :(табл. 3.2). Таблиця 3.2

(рад)	0,5	0,125	0,01	0,005
	0,958851	0,997398	0,999983	0,999996

Складається враження, що границя функції при існує і дорівнює 1.

Строге доведення цього глибокого факту ґрунтується на теоремі про граничний перехід у нерівності, яка застосовується для нерівності . Отже,

.

О скільки , а , то і, отже, графік функції має такий вигляд (рис. 3.8):

Рис.5			Смисл першої важливої границі полягає у тому, що синус малого кута практично дорівнює величині цього кута (у радіанах)
		, .

Друга важлива границя. Функція 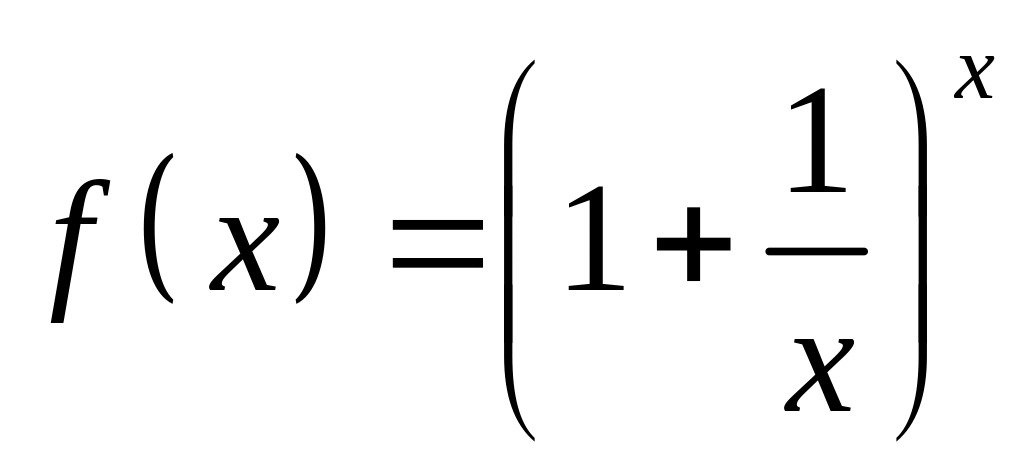зростає при (у це можна повірити, шляхом обчислення на калькуляторі значеннь , , , ).

Крім того, неважко показати, що ця функція обмежена при : . Тоді на підставі твердження теореми про те, що зростаюча та обмежена функція має скінченну границю, робимо висновок, що функція має границю при , яку прийнято позначати буквою (рис.6). Число є ірраціональним і навіть трансцендентним. Отже, мають місце співвідношення

.	.
Рис.6		Зокрема , . Логарифми за основою називаються натуральними і позначаються . Перша та друга важливі границі дозволяють суттєво розширити запас еквівалентних нескінченно малих величин.

Таблиця еквівалентних нескінченно малих функцій

При справедливі асимптотичні рівності, подані у табл.1:

Таблиця 1

1.	2.
3.	4.
5.	6.
7.	7 .
8.	8 .

Приклад 11. Користуючись правилом заміни еквівалентними нескінченно малими, знайти такі границі:

1) 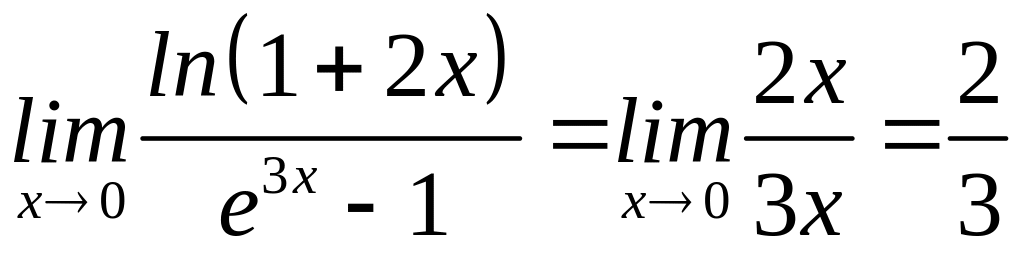(використовували формули 8 та 7 табл.1);

2) (використовували формули 1 та 8 табл.1);

3) 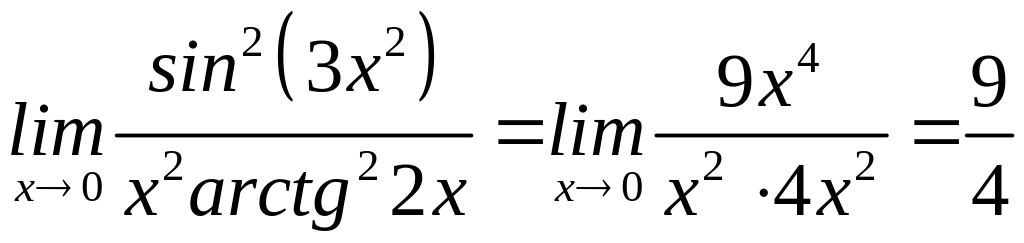(використовували формули 1 та 5 табл.1);

4) 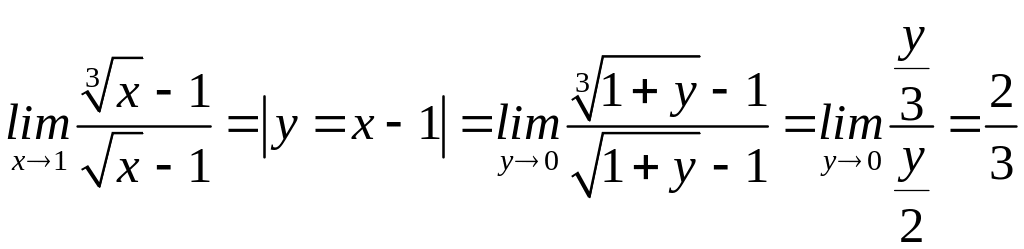(викор-ли форм. 6 табл.1);

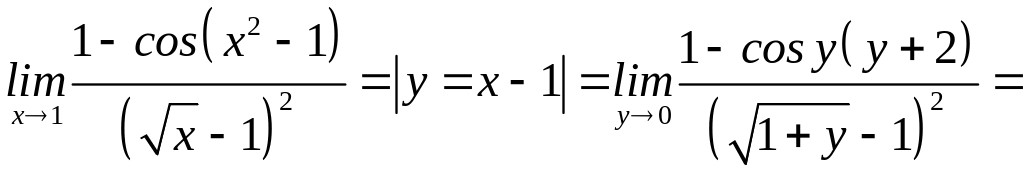
5) 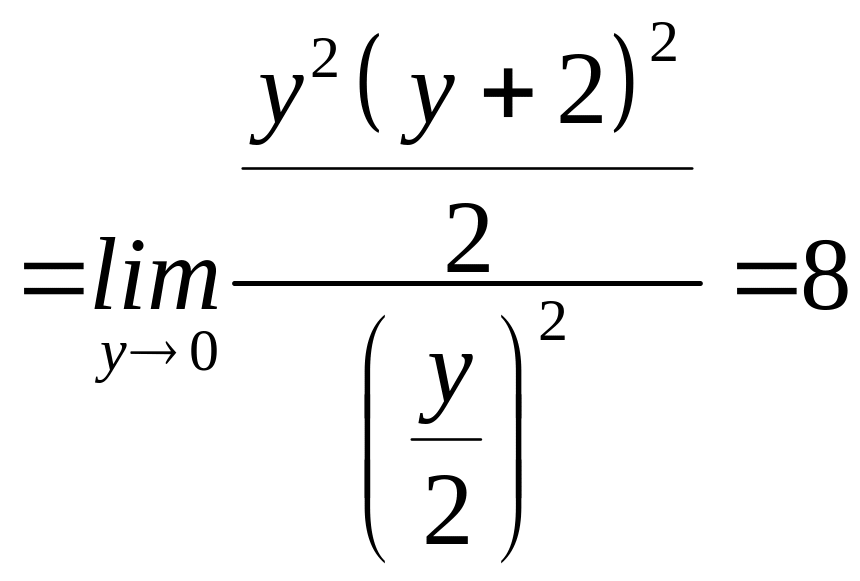(фор мули 3 та 6 табл.1);

6) 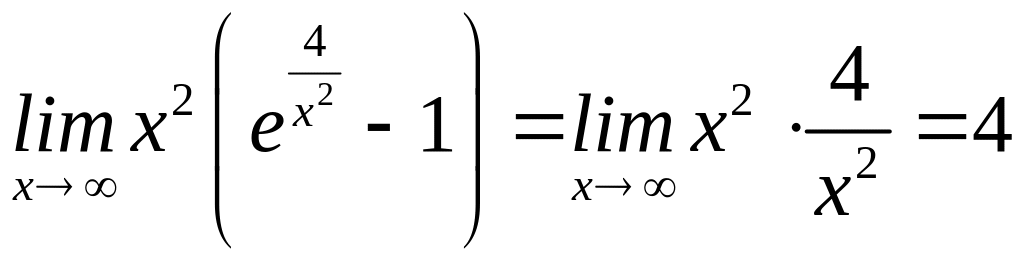(використовували формулу 8 табл.1);

7) 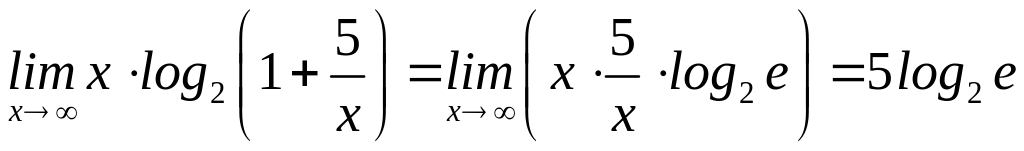(формула 7¢ табл. 1).

При знаходженні границь степенево-показникових функцій корисно використовувати основну логарифмічну тотожність

;

Якщо ,то та (5)

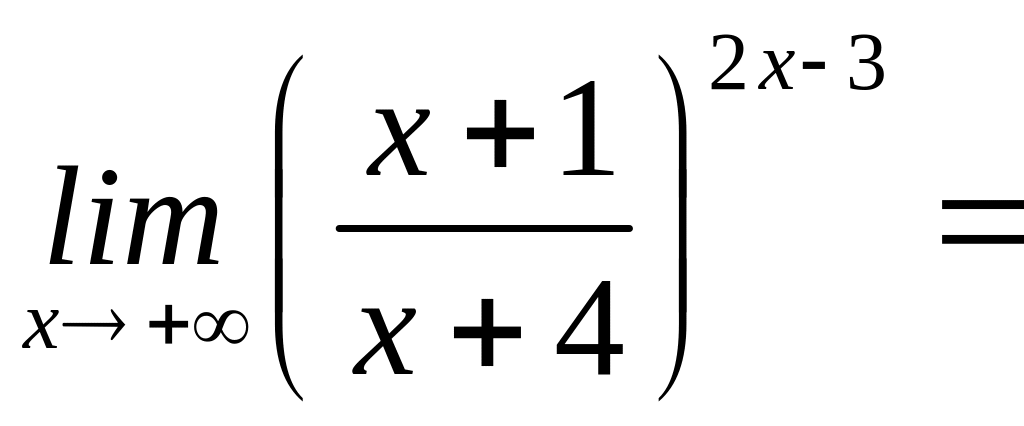
8) 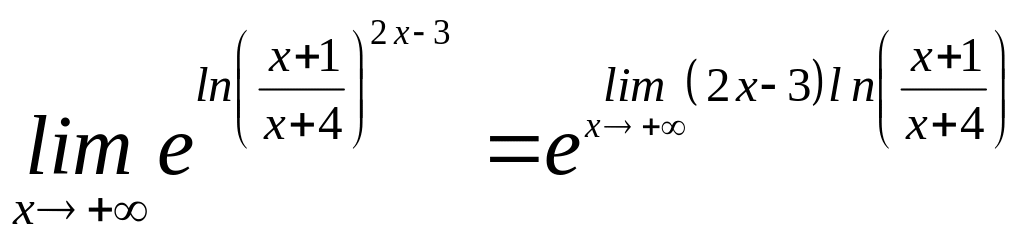= , оскільки

1. = =. = =

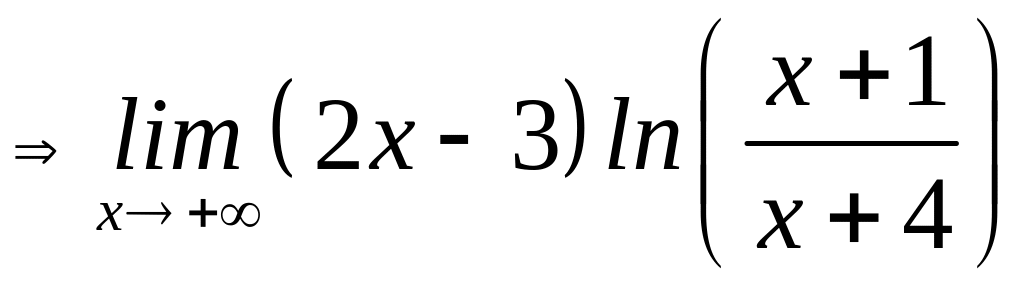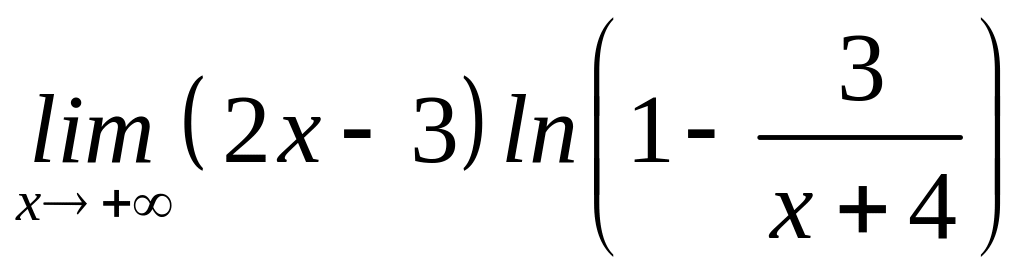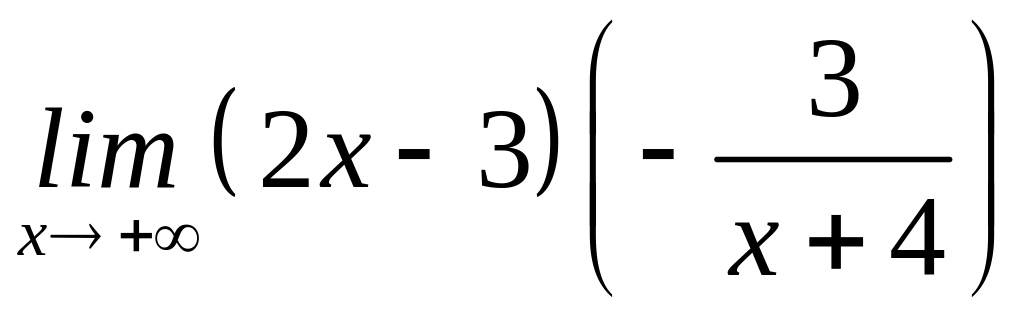9) = ,

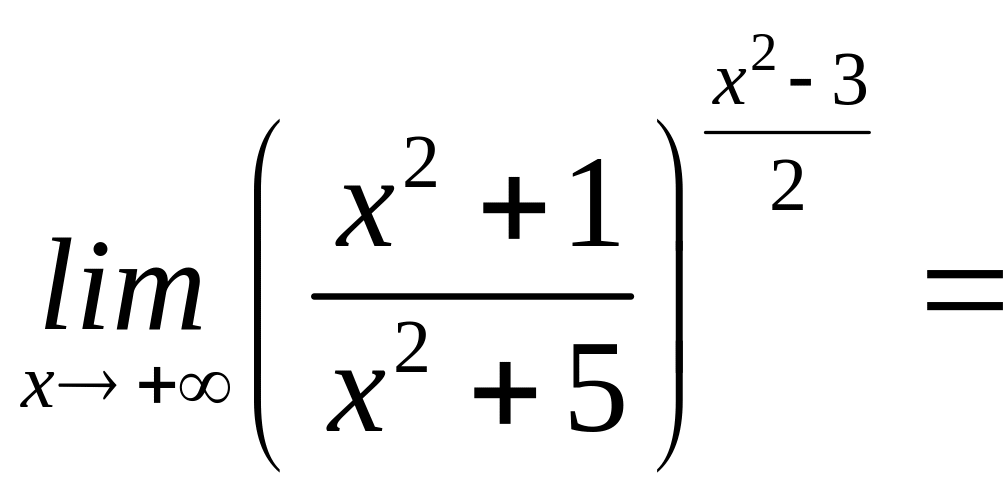
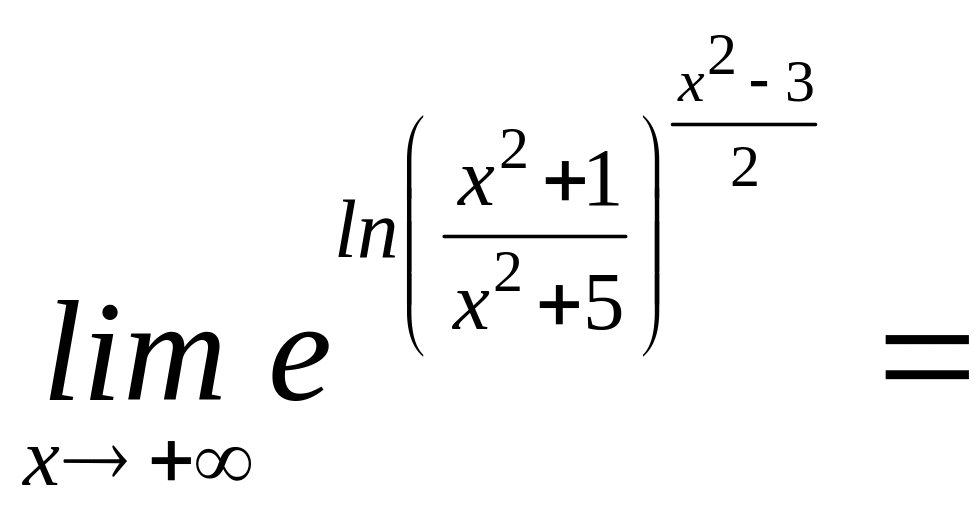
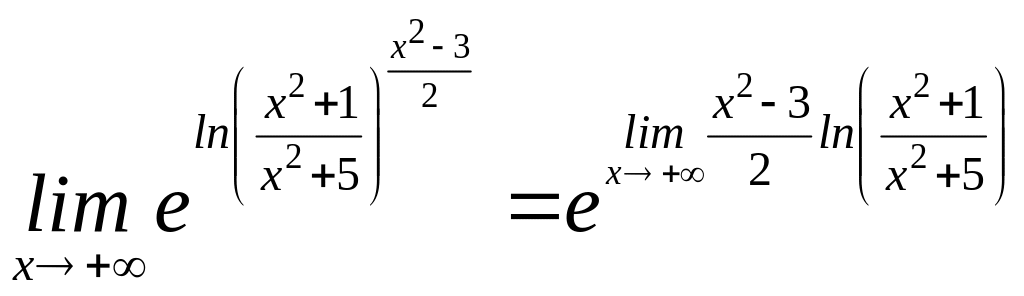оскільки = = = =

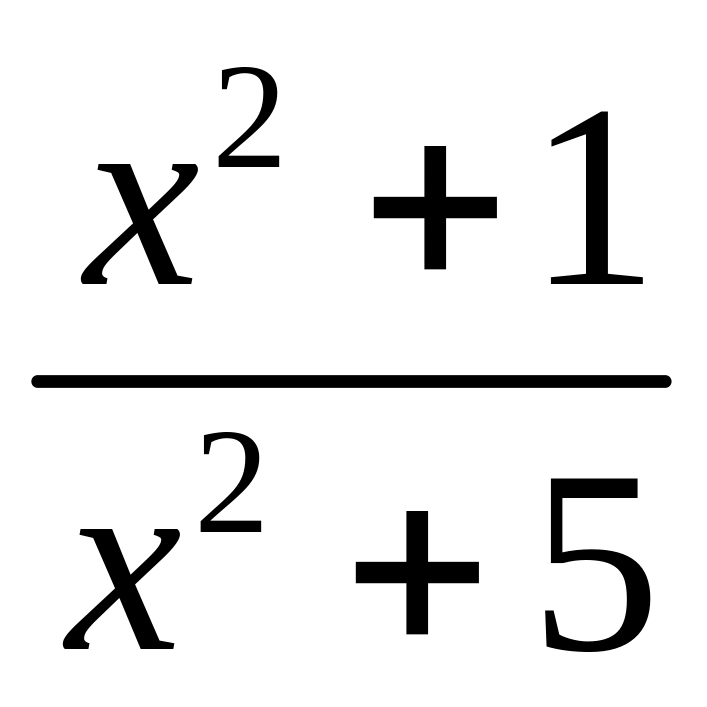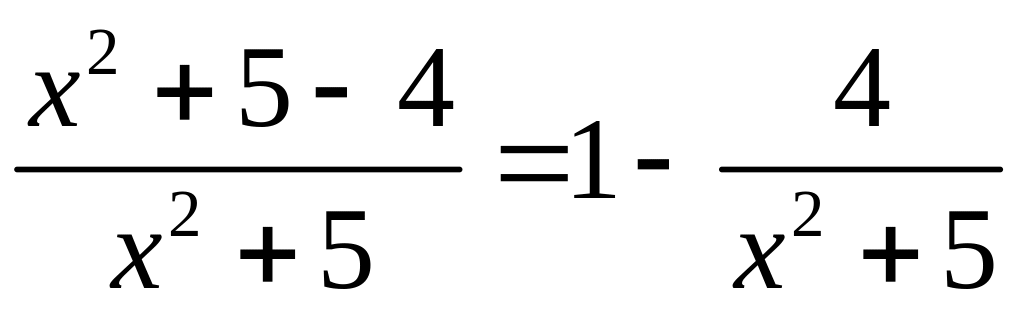
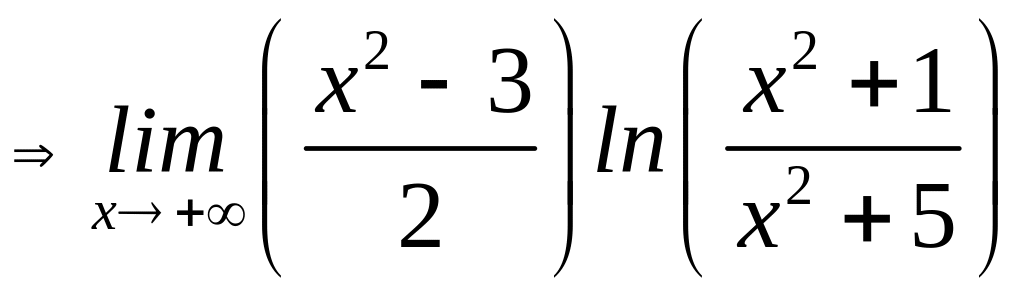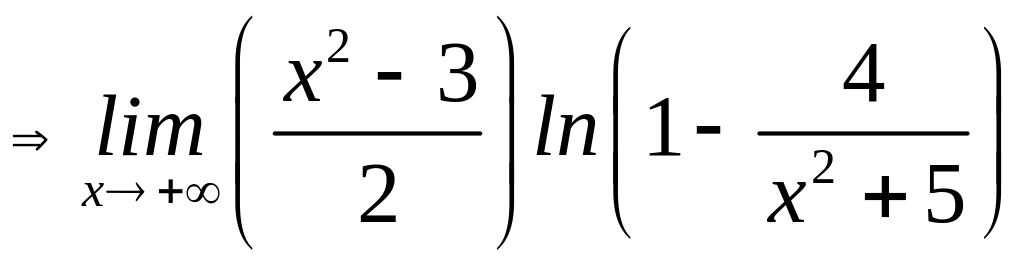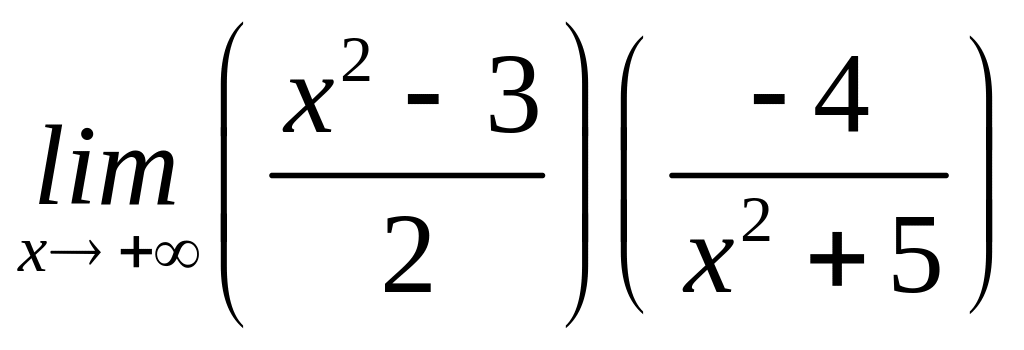10) ,

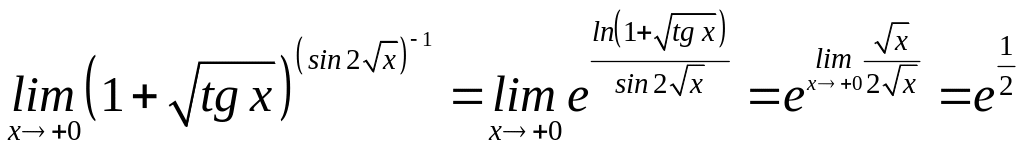тут була застосована формула (5)та формули 1, 2, 7 табл.1;

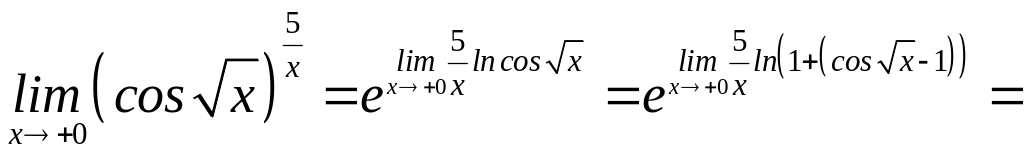
11) (використовували формулу (5) та формули 3 та 7 табл. 1);

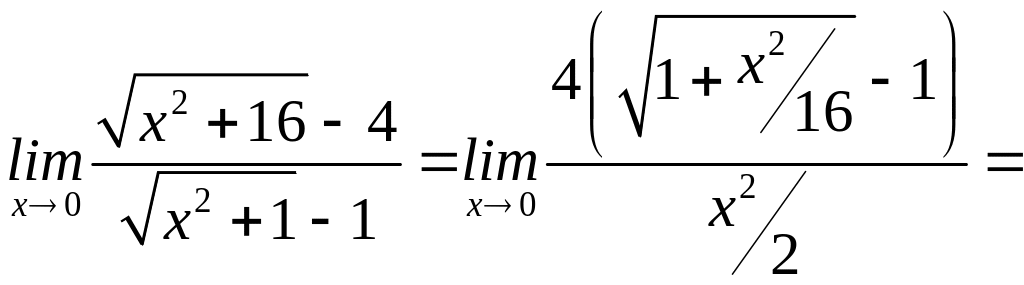
12) 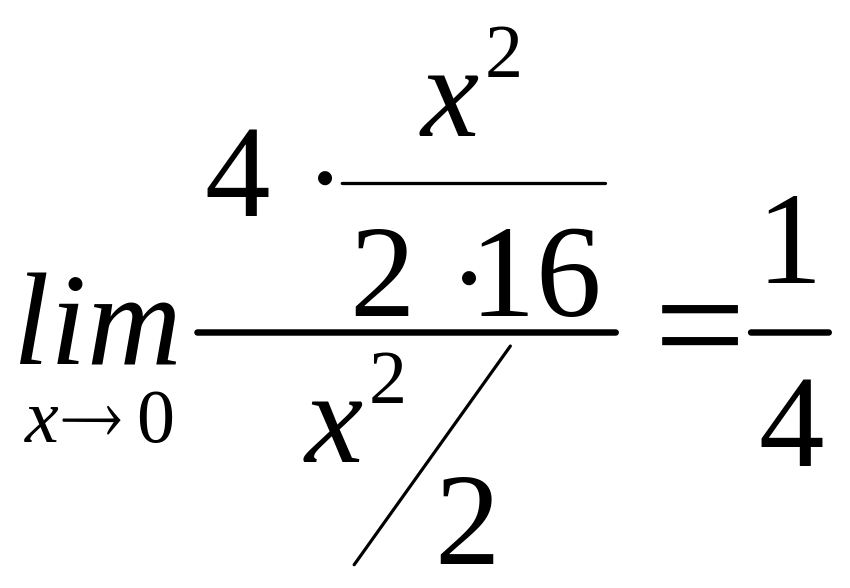(використ-ли форм.6табл. 1);
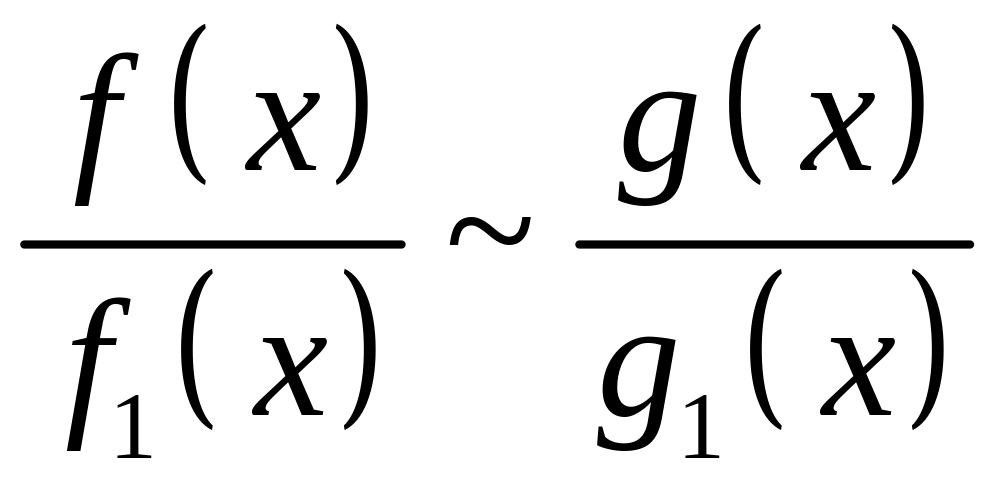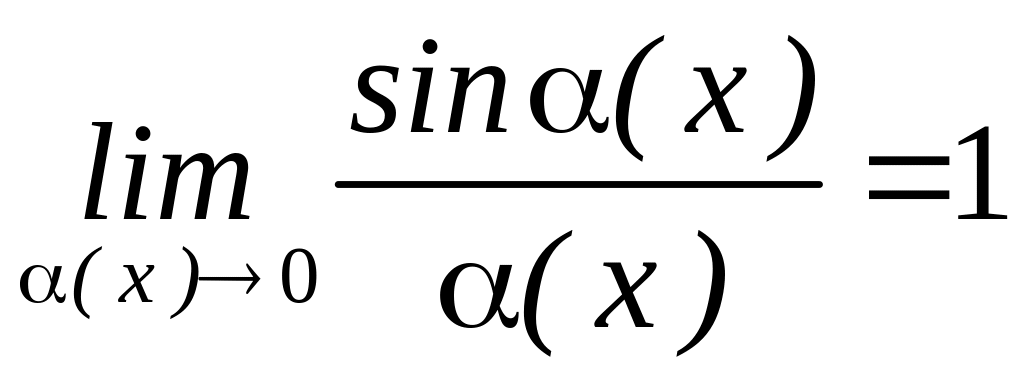
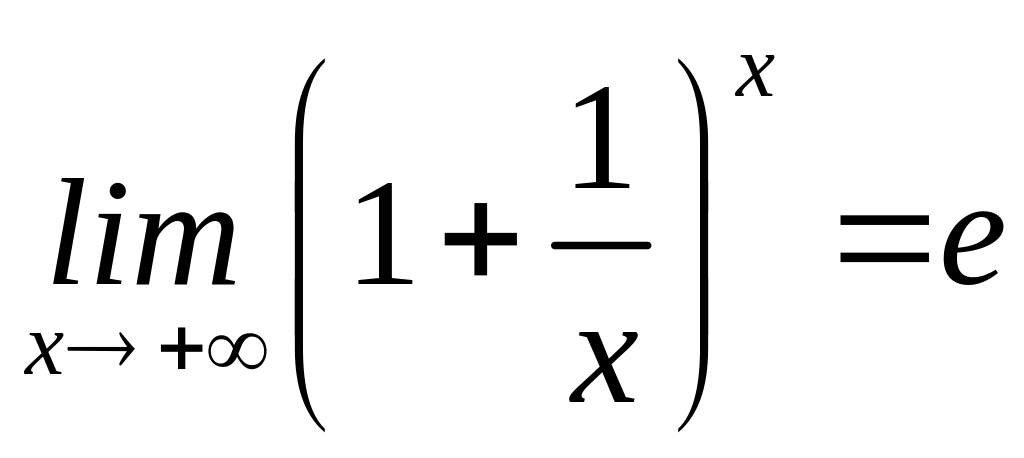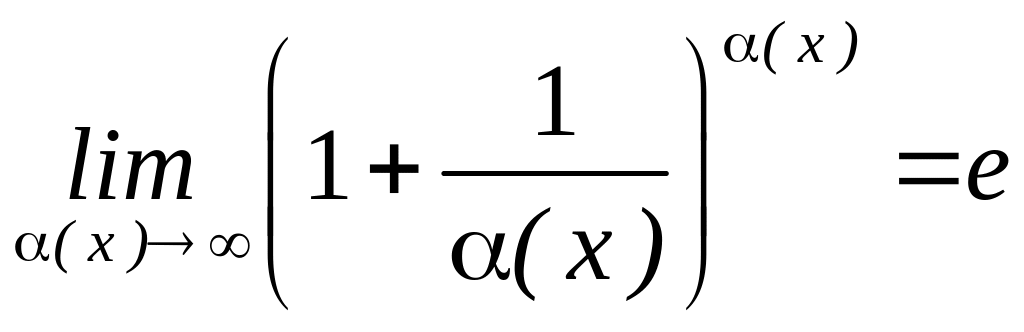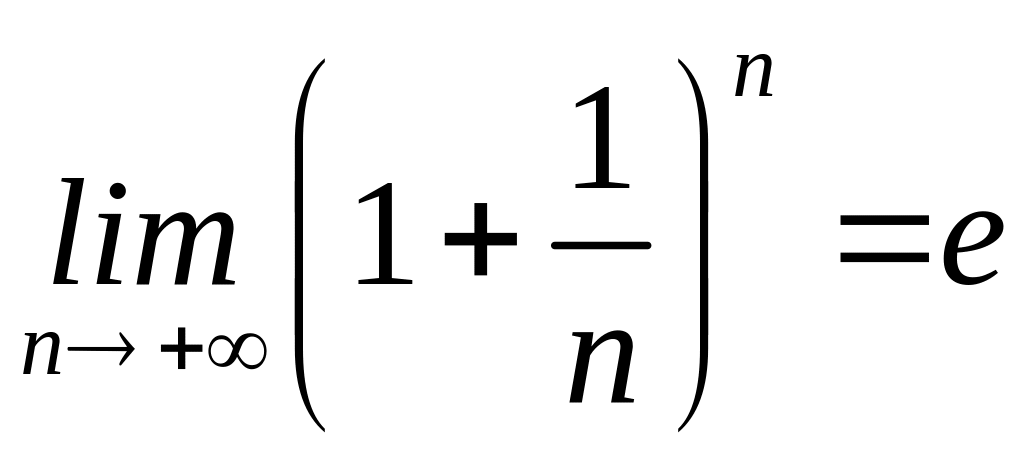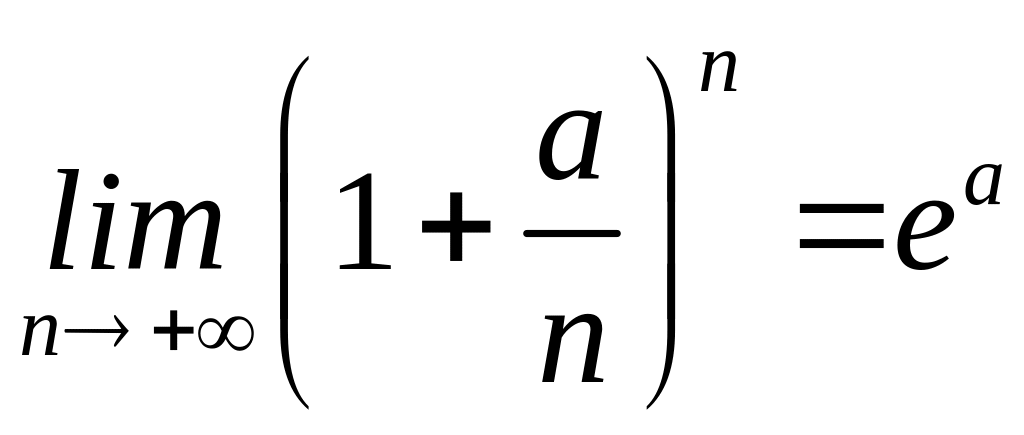