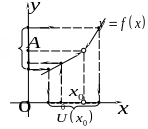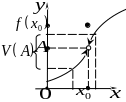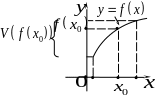- •2.Диференціальне числення
- •1. Границя функції
- •1.Інтуїтивне означення границі
- •2.Нескінченні границі
- •3.1. Скінченна границя функції у точці.Точне означення
- •3.3. Однобічні границі
- •3.4. Послідовність та її границя
- •3.Розкриття невизначенностей
- •4. Нескінченно малі та нескінченно великі функції
- •2.8. Деякі факти математичної логіки
- •Неперервність
- •4.1. Неперервні функції
- •4.2. Розривні функції
- •4.3. Властивості неперервної функції
- •5.1. Відносний приріст функції
- •5.3. Тлумачення похідної
- •1) Геометричний зміст похідної.
- •5.4. Правила диференціювання (знаходження похідних)
- •5.6. Диференціал функції
- •5.7. Похідні та диференціали вищих порядків
2.Диференціальне числення
1. Границя функції
1.Інтуїтивне означення границі
Почнемо
з інтуїтивного
означенням границі. Поняття границі
пов'язане з вивченням поведінки функції
![]() в зв'язку з поведінкою її аргумента
в зв'язку з поведінкою її аргумента
![]() .
Ставиться питання про те, як поводить
себе змінна
,коли
змінна
необмежено наближається до деякої
сталої
.
Ставиться питання про те, як поводить
себе змінна
,коли
змінна
необмежено наближається до деякої
сталої
![]() .
Якщо при наближенні змінної х до сталої
функція
також наближається до деякої сталої
.
Якщо при наближенні змінної х до сталої
функція
також наближається до деякої сталої
![]() ( не припускається, що
визначена при
=
,
наприклад
( не припускається, що
визначена при
=
,
наприклад
![]()
![]() ),
то вважається, що
прямує до границі
при
),
то вважається, що
прямує до границі
при
![]() .
У виглялі формули
.
У виглялі формули
![]() .
.
Функції, які вивчались у середній школі називаються елементарними.
Т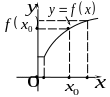 еорема
1. Якщо елементарна
функцію визначена у точці
,
то
еорема
1. Якщо елементарна
функцію визначена у точці
,
то
![]() .
.
Рис.1 |
Рис.2 |
Цей
випадок ілюструється на рис.1. На рис 2
подано графік парної функції
![]()
![]() ,яка
не визначена у точці
=0,
але границя цієї функції у точці
=0
існує та дорівнює 1.
,яка
не визначена у точці
=0,
але границя цієї функції у точці
=0
існує та дорівнює 1.
Приклад 1. Обчислити границі:
а)
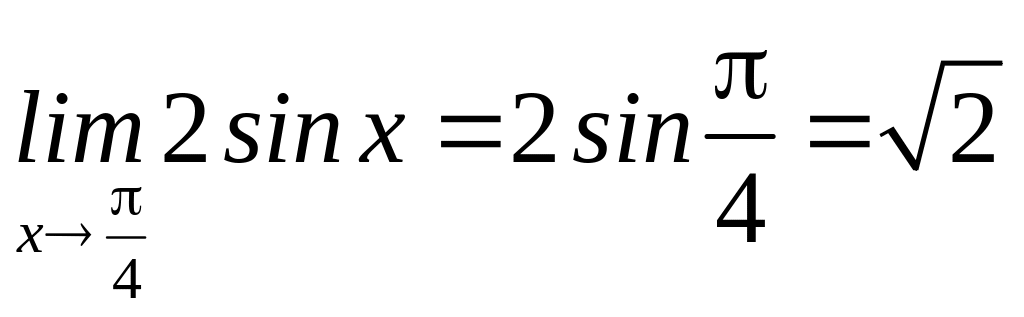 ;
б)
;
б)
![]() ;
в)
;
в)
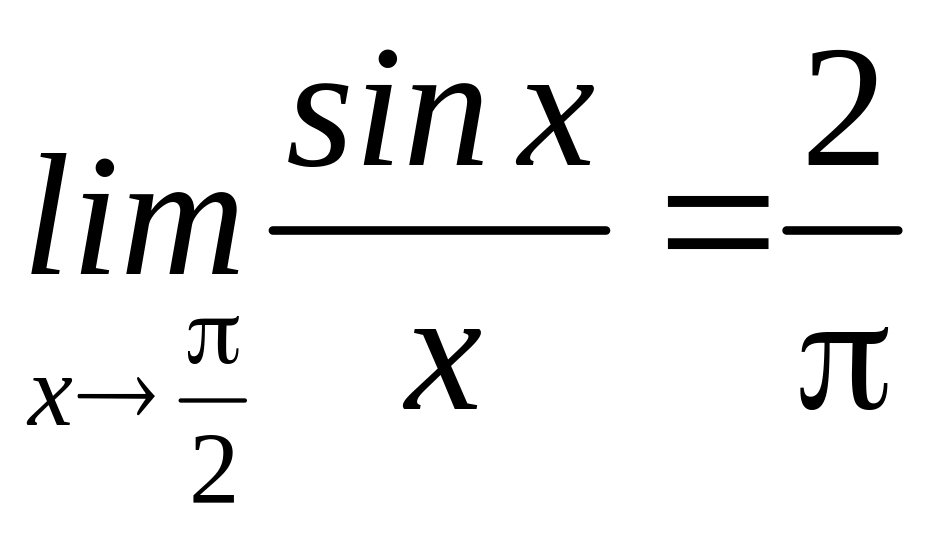 .
.
2.Нескінченні границі
Означення. Змінна
величина прямує до
![]() (нескінченності), якщо вона стає та
залишається більшою скільки завгодно
великого наперед заданного числа.
(нескінченності), якщо вона стає та
залишається більшою скільки завгодно
великого наперед заданного числа.
Приклад
2. По графіках функцій
![]() (рис.3)видно,
що вони
(рис.3)видно,
що вони
![]() при
при
![]() .
Взагалі
.
Взагалі
![]() при
,
якщо
при
,
якщо
![]() .
.
![]() (1)
(1)
Рис.3 |
Рис.4 |
Приклад 3.
По графіках функцій
|
3.1. Скінченна границя функції у точці.Точне означення
Поняття границі виникає у результаті розв’язання багатьох прикладних задач (площа фігури, швидкість точки і т. д.) і є фундаментом, на який спирається більшість розділів природознавства.
Перейдемо до точних означень.
О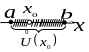 значення
1. Околом
значення
1. Околом
![]() точки
точки
![]() називається довільний інтервал, який
містить цю точку. Проколеним
околом
називається довільний інтервал, який
містить цю точку. Проколеним
околом
![]() точки
точки
![]() називають окіл
точки, з якого виключена сама точка
.
У будь-якому околі точки
вміщується симетричний
називають окіл
точки, з якого виключена сама точка
.
У будь-якому околі точки
вміщується симетричний
![]() - окіл
- окіл
![]() цієї точки, тобто сукупність точок
вигляду
цієї точки, тобто сукупність точок
вигляду
![]()
![]() .
.
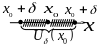

Нехай
функція
![]() визначена у проколеному околі
визначена у проколеному околі
![]() точки
.
точки
.
Означення
2. Число
![]() називається границею
функції
у точці
(при
,
що прямує до
),
якщо для будь-якого околу
називається границею
функції
у точці
(при
,
що прямує до
),
якщо для будь-якого околу
![]() числа
знайдеться такий проколений окіл
числа
знайдеться такий проколений окіл
![]() точки
,
що для всіх
точки
,
що для всіх
![]() значення
функції
значення
функції
![]() (рис. 3.1).
(рис. 3.1).
(Значення
виключається для того, щоб подане вище
означення можна було використовувати
як у тому випадку, коли функція
в точці
невизначена (рис. 3.1,а), так і у тому, коли
![]() (рис. 3.1,б)).
(рис. 3.1,б)).
a |
б |
|
|||
в Рис. 3.1 |
Якщо – границя функції , коли прямує до , то використовують такі позначення:
За допомогою логічних символів означення скінченної границі функції у точці записується таким чином: |
||||
|
|
|
|
Можна довести, що в тому випадку, коли елементарна функція визначена в точці , знаходження границі не викликає труднощів:
|
Приклад 1. Обчислити границі:
а) ; б) ; в) .
Оскільки
в кожному околі точки
міститься її деякий симетричний окіл,
то в поданому вище означенні скінченної
границі можна замінити околи
і
відповідно на
![]() і
і
![]() .
З геометричної точки зору це відповідає
тому, що графік функції
для
.
З геометричної точки зору це відповідає
тому, що графік функції
для
![]() лежить у горизонтальній смузі, ширина
якої
лежить у горизонтальній смузі, ширина
якої
![]() з центром в
.
з центром в
.
Приклад
2. Обчислити
![]() .
.
Розв’язання.
Функція
![]() не визначена при
не визначена при
![]() .
Покаже-
.
Покаже-
мо,
що границя цієї функції при
![]() існує і дорівнює 0. Нехай
існує і дорівнює 0. Нехай
![]() ,
тоді для
,
тоді для
![]()
![]() значення
значення
![]()
![]()
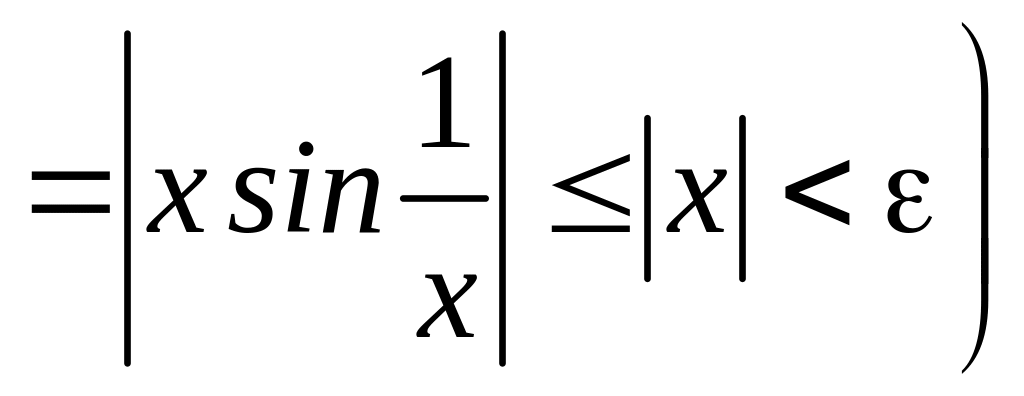 .
Отже,
.
Отже,
![]() .
.
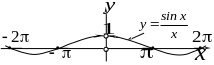
Відзначимо, що
неперіодична функція
![]() не має границі при
.
Значення цієї функції коливаються між
не має границі при
.
Значення цієї функції коливаються між
![]() та
та
![]() .
При наближенні
до
.
При наближенні
до
![]() коливання функції стають все частішими
(див. приклад 9, розділ 2).
коливання функції стають все частішими
(див. приклад 9, розділ 2).

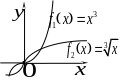
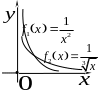
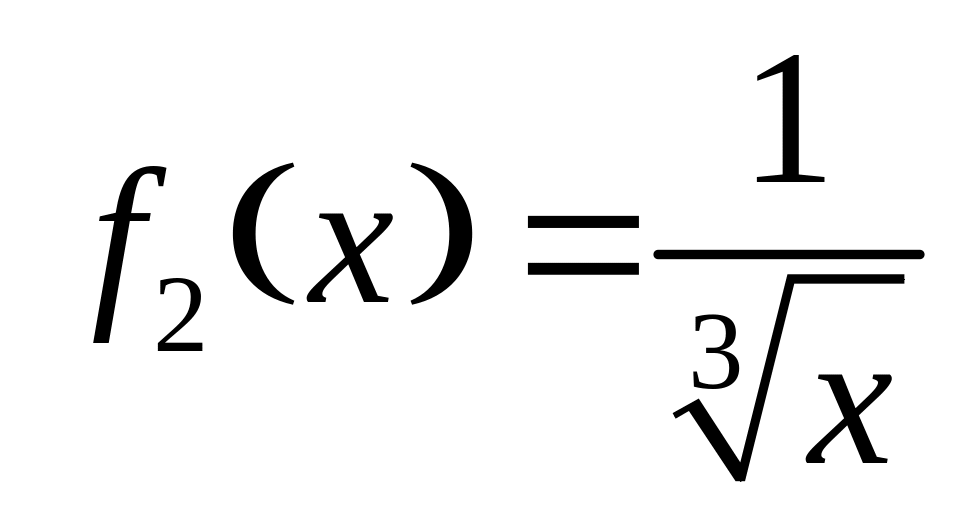 видно,
що вони
видно,
що вони