2. Теорема Крамера.

Розглянемо випадок, коли в системі (5.1) число рівнянь дорівнює числу невідомих і . Таку систему будемо називати системою Крамера.

Теорема. Система Крамера має єдиний розв'язок , який задається формулою

, (3.3)

де -матриця, одержана з матриці заміною і-ого стовпця стовпцем вільних членів.

Відзначимо, що формулу Крамера (3.3) на практиці не використовують для розв'язку систем лінійних рівнянь з великою кількістю невідомих, оскільки вони потребують значного об'єму обчислювальної роботи.

Приклад 1. Розв'язати за формулами Крамера систему рівнянь

(у матричній формі )

Розв'язання.Оскільки

= ,то розглянута система є системою Кpамера.

Формула (3.3) приводить до наступної схеми розв'язку:

,

,

,

3.Обернена матриця.

Нехай - квадратна матриця порядку .

Означення 2. Оберненою матрицею для матриці -го порядку називається матриця така, що

Матриця існує та єдина тоді і тільки тоді, коли (матриці, визначники яких не дорівнюють нулю називаються не- виродженими, а якщо то виродженими).

Алгоритм обчислення оберненої матриці є такий.

1. Обчислюється .

2. Утворюється матриця з алгебраїчних доповнень елементів матриці А, яка позначається

(3.4)

3. Транспонування матриці . Матриця називається приєднаною матрицею для матриці

. (3.5)

4. Матриця визначається формулою

(3.6)

Приклад 2. За даною матрицею знайти її обернену .

a) б) ; в)

Розв'язання. а) ,

.

б) Для цієї матриці обчислений у прикладі 3, а) з §2, а алгебраїчні доповнення у прикладі 2,б), §2. Таким чином,

, , .

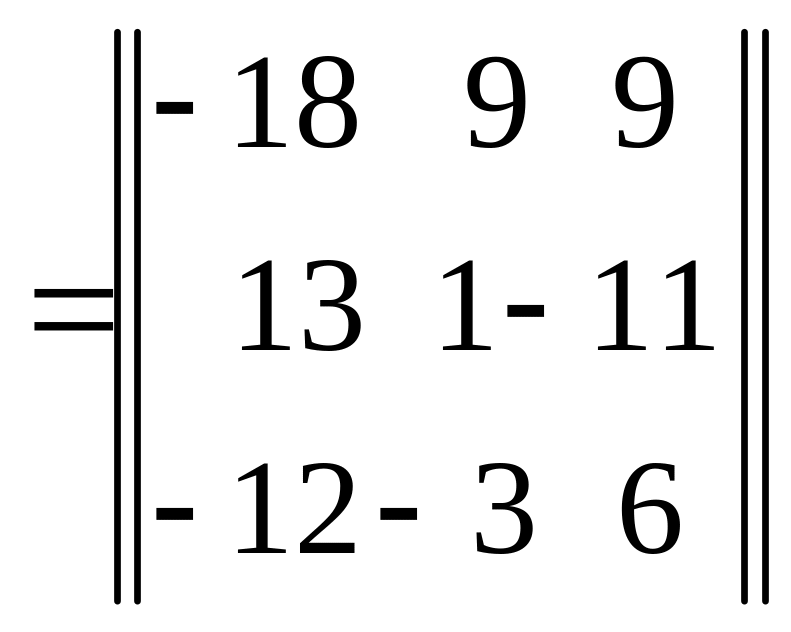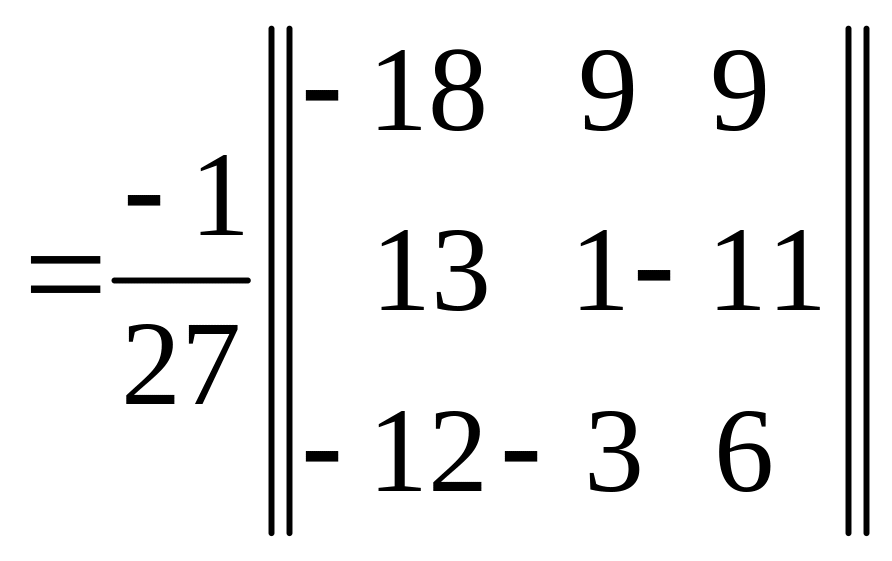Перевірка .

в) .

=8, =5, =–1, =–29, = = = = =2

і, отже, .

4.Матричний спосіб розв'язання слар

Матричний запис системи (3.1)

. (3.2)

Нехай та . Тоді можна знайти обернену матрицю . Помножимо обидві частини рівності (3.2) на та одержимо

, (3.7)

Формула (3.7) визначає матричний спосіб розв'язання СЛАР:

1. Знайти матрицю ;

2. Знайти розв'язок системи (3.1) за формулою (3.4)

Приклад 2. Розв'язати систему з прикладу 1 матричним спосо-бом. (у матричній формі )

Розв'язання. 1) .

2) Обчислюємо алгебраїчні доповнення елементів матриці :

= = , = = , = = ,

= = , = = , = = ,

= = , = = , = = .

3) За формулами (3.4)-(3.6) одержуємо:

, , .

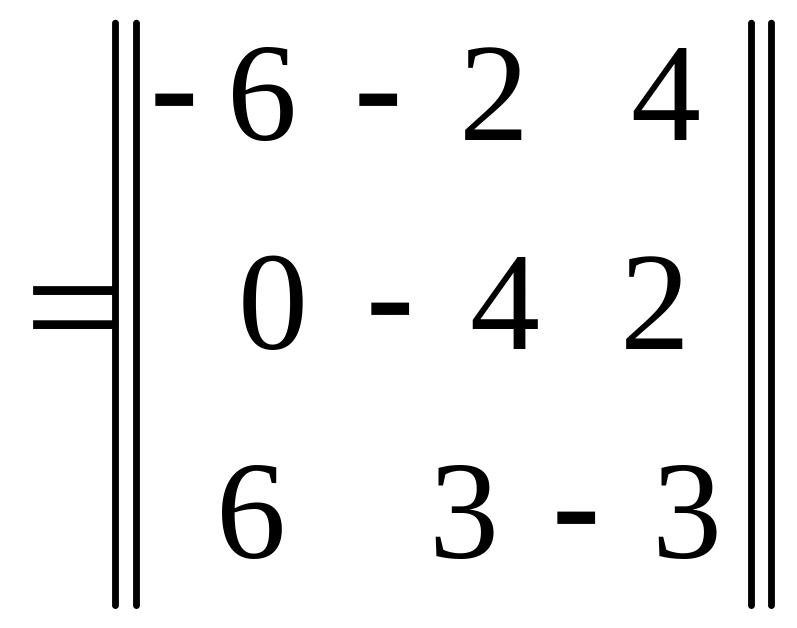4) За формулою (3.7):

.

Отже,

З. Метод Гаусса.

Цей метод послідовного виключення невідомих є практичним засобом розв'язання системи лінійних рівнянь з невідомими.

Він полягає в тому що за допомогою елементарних перетворень система рівнянь перетворюється до еквівалентної системи трикутного (або трапецієвидного вигляду, з якої послідовно, починаючи з останніх за номером змінних знаходяться усі інші змінні.

При розв'язанні системи (3.1) виникають три випадки. 1) Система, що розглядається є

системою Крамера та має єдиний розв'язок. 2) Випадок несумісної системи. 3) Система

має нескінченну множину розв'язків. Метод Гаусса розглянемо на прикладах.

1. Система Крамера, =3, .

розв'язок системи (-3; 2; 5).