9.3.3. Оптимизация структуры объектов проектирования

Каждый объект проектирования состоит из целого ряда звеньев. Достаточно часто необходимые звенья существуют в ряде вариантов. При этом ставится задача — какой вариант звеньев и в каком количестве необходимо принять, чтобы объект проектирования имел оптимальную структуру. Как и раньше, возможны две постановки задачи оптимизации.

Первая постановка:

Вторая постановка:

В дальнейшем детализацию постановки будем производить для первой постановки; работы по второй постановке выполняются аналогично.

Алгоритм 9.3.3. Последовательность работ при оптимизации структуры объекта проектирования

1. Содержательная постановка задачи оптимизации.

2. Представление структуры объекта проектирования в виде набора типов элементов и вариантов, как это показано на рис. 9.3.16.

Рис. 9.3.16

3. Обозначения параметров элементов показаны на рис. 9.3.17.

Рис.9.3.17

4. Математическая постановка задачи в общем случае имеет вид:

(9.3.14)

где С (ОП) — стоимость объекта проектирования,

c_j — стоимость j-го элемента,

x_j — количество j-ых элементов,

Т (ОП) — технические параметры объекта проектирования,

t_j — технические параметры j-го элемента,

F(x_j) = 0 — зависимость между числом различных элементов,

Т_зад (ОП) — задаваемое значение технических параметров объекта проектирования.

Поскольку в (9.3.14) накладывается требование x_j —целые, то система (9.3.14) представляет собой задачу целочисленного программирования.

5. Определение зависимостей, входящих в (9.3.14).

6. Ввод условий задач в Excel.

7. Решение задачи.

8. Анализ задачи.

Работу по данному алгоритму проиллюстрируем на следующем примере.

1. Содержательная постановка.

Требуется выбрать структуру звуковоспроизводящего комплекса.

2. Комплекс должен включать два типа аппаратуры: низкочастотную и высокочастотную.

Рис. 9.3.18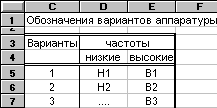

Обозначения типов аппаратуры и ее вариантов приведены на рис. 9.3.18.

3. Значения параметров элементов приведены на рис. 9.3.19.

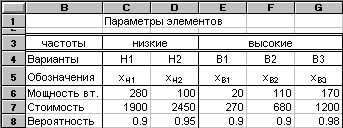
Рис. 9.3.19

4. Математическая модель имеет вид (9.3.14).

5. Определение зависимостей, входящих в (9.3.14):

Стоимость: .

Мощность: .

Вероятность безотказной работы: .

Зависимость F(x_j) = 0 задается в виде двух зависимостей:

• Общее число низкочастотной аппаратуры задается в виде: х_н1 + х_н2  2.

• Отношение количества высокочастотной аппаратуры к низкочастотной должно удовлетворять требованию:

,

Т_зад(ОП) = W_зад,

Тогда математическая постановка задачи будет иметь вид:

(9.3.15)

Система (9.3.15) является нелинейной, следовательно, решаемая задача представляет собой целочисленную задачу нелинейного программирования.

6. Ввод условий задачи в Excel.

Ввод условий задачи включает ввод зависимостей из (9.3.15) и значений параметров, приведенных на рис. 9.3.19. При этом приняты значения W_зад = 300, Р_зад = 0,70. Введенные данные показаны на рис. 9.3.20.

Рис. 9.3.20

7. Решение задачи и ее анализ.

Принимаем х_j⁰ = 1 и далее решаем задачу нелинейного целочисленного программирования по алгоритмам, рассмотренным в главе 5. Результат решения задачи представлен на рис. 9.3.21.

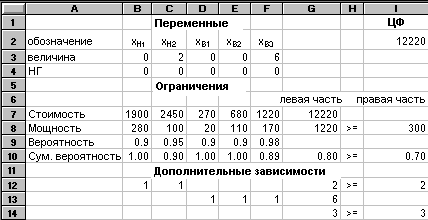
Рис. 9.3.21

Как и в предыдущем разделе, анализ задачи, о котором говорилось уже неоднократно, выполнять не будем.

Приведенные примеры наглядно показывают преимущества оптимального проектирования, реализованного средствами Excel 7.0.