5. Расчет в одном контрольном положении кинематических характеристик механизма.

Для выполнения данных расчетов нам необходимо знать следующие величины:

м;

м ;

м.

Данный алгоритм используем для заданного контрольного положения при =11, при котором угол φ₁=60⁰.Результаты расчетов и ход расчетов отображены в следующей таблице.

Таблица 3.2. Результаты расчета аналитического метода.

Парамет ры	Формула	Размерность	Результат
xA		м	0,031
yA		м	0,054
хB		м	0,312
		-	0,979
		-	-0,188
		-	-0,110
		м	-0,059
		-	0,191
		-	-0,024
		м	0,124
		м	0,036
		м	-0,056
		м	0,021
		-	-0,029
		-	0,037
		м	0,349
		м	0,037

Сравниваем результаты расчетов, полученные графическим и аналитическим методами.

Таблица 3.3. Сравнение результатов расчетов.

Переменная		Размерность	Графический метод	Аналитический метод
хB		м	0,312	0,312
φ2		град	349	349
xS2		м	0,120	0,120
	Продолжение Таблица 3.3.
yS2		м	0,036	0,036
i21		-	-0,110	-0,110
i31		м	-0,059	-0,059
		м	-0,056	-0,056
		м	0,021	0,021
SB		м	0,037	0,037

5. Выбор динамической модели и ее обоснование.

Для упрощения решения задачи динамического синтеза машинный агрегат заменим динамической моделью в виде вращающегося звена, закон движения которого совпадает с законом движения начального звена кривошипно-ползунного механизма (кривошипа 1), т.е. обобщенная координата , угловая скорость звена приведения , угловое ускорение .

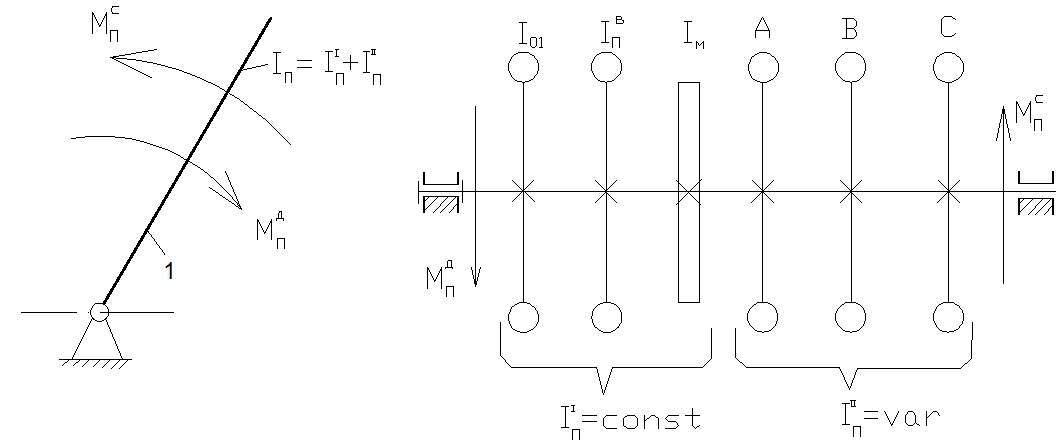
Рисунок 3.5. Динамическая модель машинного агрегата.

В качестве динамической модели рассматривается звено приведения – кривошип 1, которое имеет приведенный момент инерции- и находится под действием приведенного момента включающий следующие составляющие:

где - приведенный момент; - приведенный момент движущих сил; - приведенный момент сил сопротивления.

Приведенный момент инерции включает две составляющие:

где - приведенный момент инерции; - постоянная составляющая приведенного момента инерции; -переменная составляющая момента инерции.

В величину постоянной составляющей входят следующие составляющие:

где - собственный момент инерции кривошипа; - приведенные моменты инерции вращающихся звеньев механизма; - момент инерции маховика.

Момент инерции маховика определяется на основании заданной степени неравномерности движения звена приведения.